【教科書が読めるようになる数Ⅲ】グラフのかき方

さん

こんにちは、高校教員の『さん』です。今回は、「グラフのかき方」について詳しく説明していくよ。

生徒

今回もよろしくお願いします！！

「人より勉強に時間がかかる」と感じていませんか？

私のクラスにも、同じ悩みを抱えて苦しんでいた生徒がたくさんいました。

• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」

• 「解答の意味が理解できず、勉強が進まない」

こうした悩みを、このブログを通じて解決し、勉強の効率を一気に上げていきましょう！

例えば、今まで1時間かかっていた勉強が30分で終わるようになれば、余った時間を復習や他の科目に使えます。その結果、テストの点数が上がり、自信にもつながっていきます。

では、なぜ教科書は読みにくいのでしょうか？

それは、「正確さ」と「簡潔さ」を最優先に作られているからです。

どんな人が読んでも、同じ意味にしか取られないようにするため、説明が端的で抽象的になりがちです。

そのため、教科書の内容を理解するには、「自分で噛み砕いて考える力」が必要です。

このブログでは、私が生徒と関わる中で気づいたことや、よく寄せられる質問、つまずきやすいポイントをもとに、教科書の内容をわかりやすく解説していきます。

「噛み砕き方」がわかれば、文章はぐっと読みやすくなります！

まずは、教科書の説明を見てみましょう。

まずは教科書の説明
簡単に説明するよ
詳しく説明するよ
まとめ

まずは教科書の説明

さん

教科書の説明ではこんなふうに書かれているよ！

例題

関数 \(y=e^{-\frac{x^2}{2}}\) のグラフをかけ。

\(f(x)=e^{-\frac{x^2}{2}}\) とする。

\(f'(x)=-xe^{-\frac{x^2}{2}}\)、

\( \begin{aligned} \displaystyle f^{\prime\prime}(x) &= -e^{-\frac{x^2}{2}}-x(-xe^{-\frac{x^2}{2}}) \\ &= (x^2-1)e^{-\frac{x^2}{2}} \\ \text{} \end{aligned} \)

\(f(x)\) の増加やグラフの凹凸は、次のようになる。

\( \begin{array}{c|ccccccc} x & \cdots & -1 & \cdots & 0 & \cdots & 1 & \cdots \\ \hline y’ & + & + & + & 0 & – & – & – \\ \hline y^{\prime\prime} & + & 0 & – & – & – & 0 & +\\ \hline y & \text{下に凸に}\nearrow & \frac{1}{\sqrt{e}} & \text{上に凸に}\nearrow & 1 & \text{上に凸に}\searrow　& \frac{1}{\sqrt{e}} & \text{下に凸に}\searrow \end{array} \)

また、\(\displaystyle\lim_{n \to \infty} f(x) = 0\)、\(\displaystyle\lim_{n \to -\infty} f(x) = 0\)であるから、\(x\) 軸はこの曲線の漸近線である。

以上から、グラフの概形は、下の図のようになる。

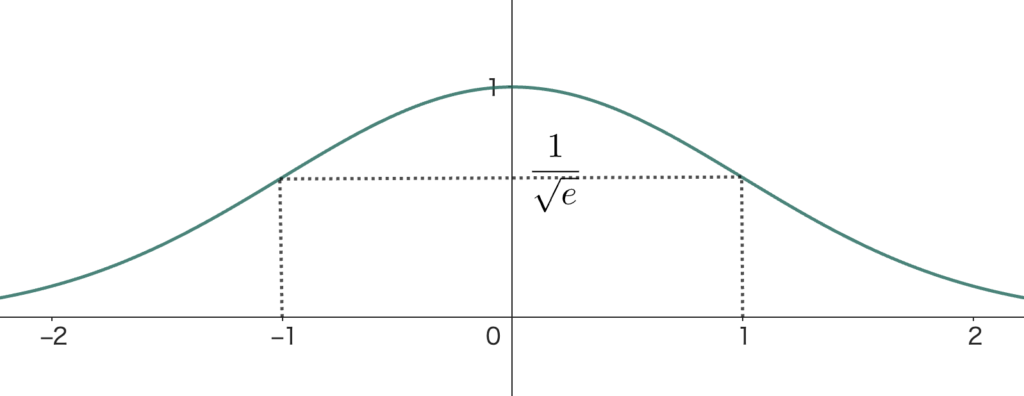
簡単に説明するよ

グラフのかき方は、

定義域を確認する
微分計算により \(y’\) や \(y^{\prime\prime}\) を計算する
\(y’=0\)、 \(y^{\prime\prime} = 0\) を求め増減表を作る
漸近線があれば図示する
グラフをかく

です。

生徒

メモメモ•••

詳しく説明するよ

数Ⅲでのグラフのかき方を説明していきます。

例題

関数 \(y=e^{-\frac{x^2}{2}}\) のグラフをかけ。

生徒

\(y=e^{-\frac{x^2}{2}}\) のグラフ? めちゃくちゃ難しそう•••

さん

これからは、どんな関数のグラフも書けるよになるよ！

次の例題を５つのステップに分けて考えていきましょう。

ステップ１：定義域を確認する

生徒

定義域ってなんだっけ？

さん

定義域は、\(x\) の範囲のことだよ！

数Ⅲでグラフを考えるときは、必ず最初に確認する癖をつけておきましょう。

定義域の主な確認ポイントは次の３つです。

定義域の主な確認ポイント

①（分母）\(\neq 0\)

② \(\sqrt{\text{0以上}}\)

③ \(\log{\text{(正)}}\)

①（分母）\(\neq 0\)

分数の分母は \(0\) にならないようにしないといけません。

例えば、関数 \(y = \frac{1}{x-1}\) の定義域は、\(x \neq 1\) です。

② \(\sqrt{\text{0以上}}\)

ルートの中身は必ず \(0\) 以上にならないといけません。

例えば、関数 \(y = \sqrt{x-1}\) の定義域は、\(x ≧ 1\) です。

③ \(\log{\text{(正)}}\)

真数は必ず正にならないといけません。

例えば、関数 \(y = \log{(x-1)}\) の定義域は、\(x > 1\) です。

定義域を確認した結果、今回の関数 \(y=e^{-\frac{x^2}{2}}\) では制限ありませんでしたね。

生徒

定義域の確認、意識してないと忘れちゃいそうだな。

さん

忘れないで！！定義域！！

ステップ２：\(y’\) や \(y^{\prime\prime}\) を計算する

生徒

\(y’\) はグラフの増減だったね。

さん

そうだね。\(y^{\prime\prime}\)では凹凸が調べられるよ。

\(y=e^{-\frac{x^2}{2}}\) を微分していきます。

\(y’=-xe^{-\frac{x^2}{2}}\)

\( \begin{aligned} \displaystyle y^{\prime\prime} &= -e^{-\frac{x^2}{2}}-x(-xe^{-\frac{x^2}{2}}) \\ &= (x^2-1)e^{-\frac{x^2}{2}} \\ &= (x+1)(x-1)e^{-\frac{x^2}{2}} \end{aligned} \)

さん

ちゃんと、因数分解した式まで変形しておこうね！

ステップ３：\(y’=0\)、 \(y^{\prime\prime} = 0\) を求め増減表を作る

\(y’=0\)、 \(y^{\prime\prime} = 0\) を求めます。

\(y’=-xe^{-\frac{x^2}{2}}=0\) とすると \(x = 0\)

\(y^{\prime\prime}=(x+1)(x-1)e^{-\frac{x^2}{2}}=0\) とすると \(x = -1, 1\)

さん

増減表の \(y’\), \(y^{\prime\prime}\) の行に \(0\) を書き込んでいこう！

\( \begin{array}{c|ccccccc} x & \cdots & -1 & \cdots & 0 & \cdots & 1 & \cdots \\ \hline y’ & & & & 0 & & & \\ \hline y^{\prime\prime} & & 0 & & & & 0 & \\ \hline y & & & & & 　& & \end{array} \)

生徒

この次は \(+\) \(-\) を書き込んでいくんだったね。

さん

\(+\) \(-\) の判断にはちょっとしたコツがあるんだ！

\(+\) \(-\) の判断のコツ

符号の変化しない部分は無視する。

例えば、\(y’=\color{hotpink}{-x}\cdot \color{deepskyblue}{e^{-\frac{x^2}{2}}}\) の \(+\) \(-\) を考えてみましょう。

今回の関数の、「符号が変化しない部分」はどこでしょうか。

それは、\(\color{deepskyblue}{e^{-\frac{x^2}{2}}}\) ですね。

\(\color{deepskyblue}{e^{-\frac{x^2}{2}}}\) は常に \(+\) です。

こういった、「符号が変化しない部分」は無視して考えることができます。

ということで、残りの \(\color{hotpink}{-x}\) の部分の \(+\) \(-\) だけ考えれば良ので、

\(x < 0\) のとき \(+\) 、\(x > 0\) のとき \(-\) となります。

生徒

一気に考えやすくなった！

さん

このコツは押さえておこうね！

では、グラフに \(+\) \(-\) を書き込んでいきましょう。

\( \begin{array}{c|ccccccc} x & \cdots & -1 & \cdots & 0 & \cdots & 1 & \cdots \\ \hline y’ & + & + & + & 0 & – & – & – \\ \hline y^{\prime\prime} & & 0 & & & & 0 & \\ \hline y & & & & & 　& & \end{array} \)

\(y^{\prime\prime}=\color{hotpink}{(x+1)(x-1)}\cdot \color{deepskyblue}{e^{-\frac{x^2}{2}}}\) の \(+\) \(-\) も同じように考えていましょう。

\(\color{deepskyblue}{e^{-\frac{x^2}{2}}}\) は常に \(+\) ですから、

\(\color{hotpink}{(x+1)(x-1)}\) の部分だけを考えればOKですね。

\(x<-1\) のとき \(+\) 、\(-1<x<1\) のとき \(-\) 、\(x>1\) のとき \(+\) 。

増減表に書き込むと、

\( \begin{array}{c|ccccccc} x & \cdots & -1 & \cdots & 0 & \cdots & 1 & \cdots \\ \hline y’ & + & + & + & 0 & – & – & – \\ \hline y^{\prime\prime} & + & 0 & – & – & – & 0 & + \\ \hline y & & & & & 　& & \end{array} \)

生徒

あとは、\(y\) の行を埋めるだけだね！

\(x = -1 \) のとき、\(y = \frac{1}{\sqrt{e}}\)

\(x = 0 \) のとき、\(y = 1\)

\(x = 1 \) のとき、\(y = \frac{1}{\sqrt{e}}\)

よって増減表は、

ステップ４：漸近線があれば図示する

生徒

漸近線ってなんだっけ？

さん

漸近線は「グラフがどんどん近づいていくけど、絶対に触れない線」のことだったね。

今までは、増減表が書けたら、グラフもかくことができました。

では、今回はどうでしょう。

こんな感じでしょうか。

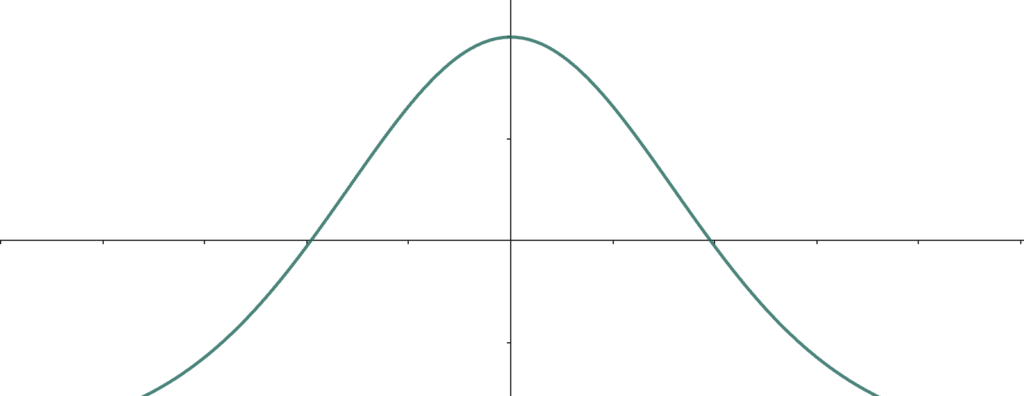
それとも、こんな感じでしょうか。

生徒

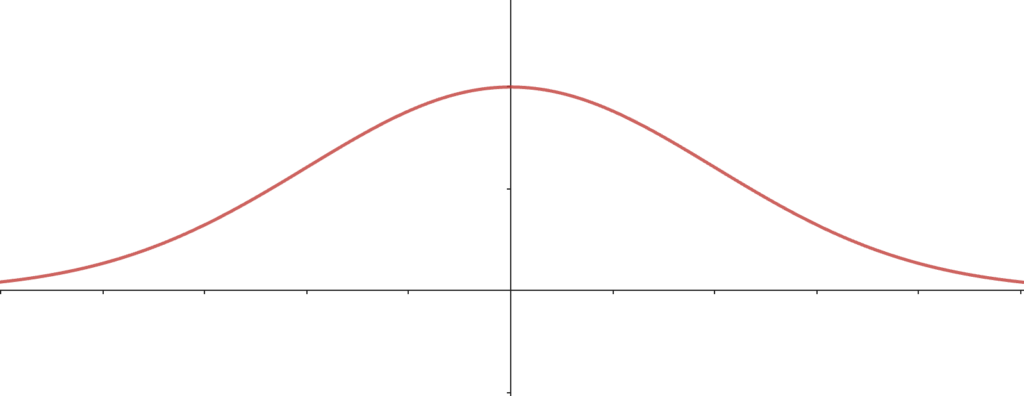
あれ？端っこってどうなってるの？

増減表からは、グラフがどこまで下がっていくのか分かりませんよね。

グラフが、\(-\infty\) まで下がっていくのか、それとも、\(0\) までしか下がらないのか。

これを確かめなければ、正確なグラフはかくことができません。

さん

\(x\)を\(\infty\)に飛ばすとどうなるのか、\(-\infty\)に飛ばすとどうなるのかを考えよう！

\(\displaystyle\lim_{n \to \infty} e^{-\frac{x^2}{2}} \) \( = \displaystyle\lim_{n \to \infty}\)\({\left(\frac{1}{e}\right)}^{\frac{x^2}{2}}\) \(= 0 \)

\(\displaystyle\lim_{n \to -\infty} e^{-\frac{x^2}{2}} \) \( = \displaystyle\lim_{n \to -\infty}\)\({\left(\frac{1}{e}\right)}^{\frac{x^2}{2}}\) \(= 0 \)

よって、グラフは右にも左にも \(0\) に近づいていくことがわかります。

つまり、「\(y=0\) がこのグラフの漸近線である」ということです。

ステップ５：グラフをかく

生徒

ここまで準備してやっとグラフがかけるのか！

さん

気を抜かないでね。最後までミスがないように！

後は、漸化式、座標軸との交点、極値、変曲点などをかき入れて、グラフを完成させましょう。

生徒

やっと完成！！

さん

お疲れ様でした！

解説

\(y’=-xe^{-\frac{x^2}{2}}\)

\( \begin{aligned} \displaystyle y^{\prime\prime} &= -e^{-\frac{x^2}{2}}-x(-xe^{-\frac{x^2}{2}}) \\ &= (x^2-1)e^{-\frac{x^2}{2}} \\ &= (x+1)(x-1)e^{-\frac{x^2}{2}} \\ \text{ } \end{aligned} \)

\(y’=-xe^{-\frac{x^2}{2}}=0\) とすると \(x = 0\)

\(y^{\prime\prime}=(x+1)(x-1)e^{-\frac{x^2}{2}}=0\) とすると \(x = -1, 1\)

\(\displaystyle\lim_{n \to \infty} e^{-\frac{x^2}{2}} \) \( = \displaystyle\lim_{n \to \infty}\)\({\left(\frac{1}{e}\right)}^{\frac{x^2}{2}}\) \(= 0 \)

\(\displaystyle\lim_{n \to -\infty} e^{-\frac{x^2}{2}} \) \( = \displaystyle\lim_{n \to -\infty}\)\({\left(\frac{1}{e}\right)}^{\frac{x^2}{2}}\) \(= 0 \)

よって、\(x\)軸が漸近線となる。