
こんにちは、高校教員の『さん』です。今日は、「定数分離を用いて、方程式の実数解の個数を求める方法」について詳しく説明していくよ。

今回もよろしくお願いします!!
「人より勉強に時間がかかる」と感じていませんか?
私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。
• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」
• 「解答の意味が理解できず、勉強が進まない」
教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。
でも大丈夫!
このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。
「噛み砕き方」がわかれば、文章はぐっと読みやすくなります!
まずは教科書の説明

教科書ではこんなふうに説明されてるよ!
一般に、方程式 \(f(x)=g(x)\) の実数解は、\(y=f(x)\) のグラフと \(y=g(x)\) のグラフの共有点の \(x\) 座標である。このことを利用すると、関数のグラフを用いて方程式の実数解について考えることができる。
\(a\) は定数とする。方程式 \(\frac{e^x}{x}=a\) の実数解の個数を求めよ。
\(f(x)=\frac{e^x}{x}\) とすると \(f'(x)=\frac{(x-1)e^x}{x^2}\)
\(f(x)\) の増減表は下のようになる。
また、
\(\displaystyle\lim_{n \to \infty} f(x) = \infty\)
\(\displaystyle\lim_{n \to -\infty} f(x) = 0\)
\(\displaystyle\lim_{n \to +0} f(x) = \infty\)
\(\displaystyle\lim_{n \to -0} f(x) = -\infty\)
よって、\(y=f(x)\) のグラフは、下の図のようになる。
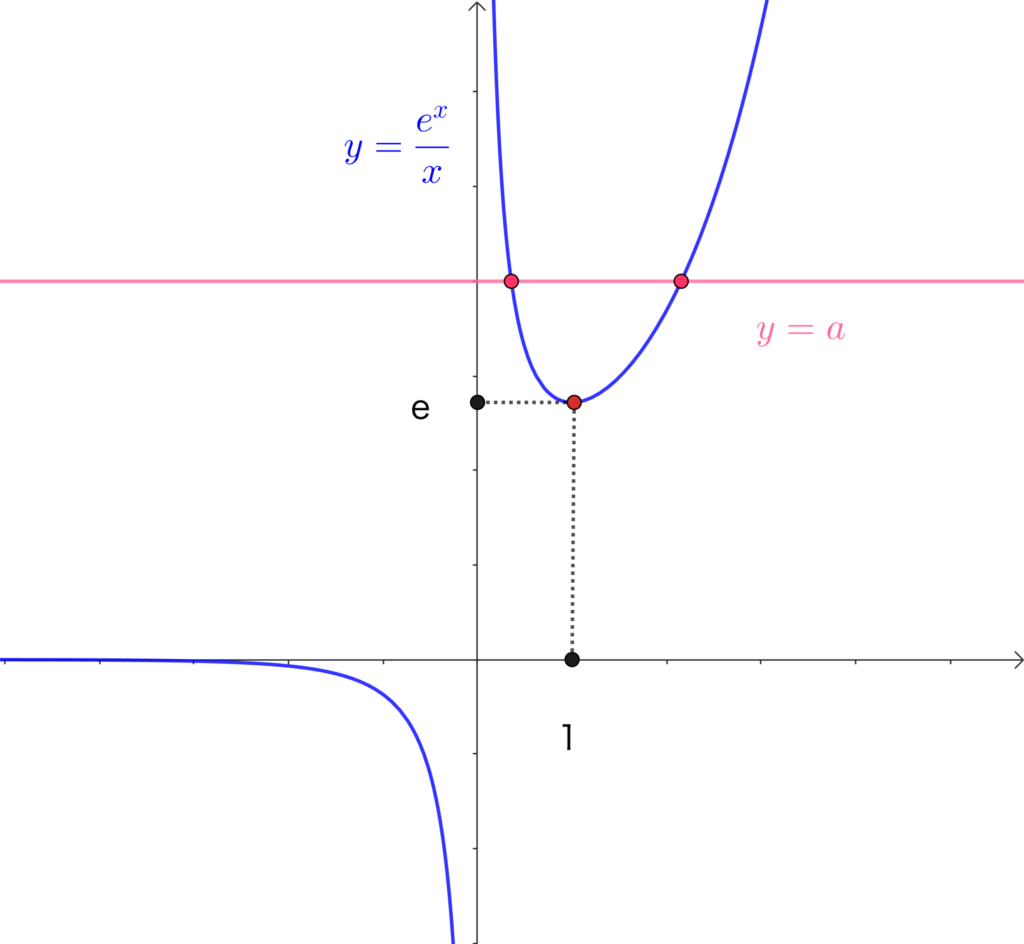
このグラフと直線 \(y=a\) の共有点の個数は、求める実数解の個数と一致する。
したがって、実数解の個数は
\(a>e\) のとき \(2\) 個
\(a=e,\) \(a<0\) のとき \(1\) 個
\(0≦a<e\) のとき \(0\) 個
簡単に説明するよ
方程式 \(f(x) = g(x)\) の実数解の個数を求める方法は
\(y = f(x)\) と \(y = g(x)\) の共有点の個数を考える
です。

メモメモ•••
詳しく説明するよ
「方程式の実数解の個数」を考える方法を説明していきます。

判別式Dを使えば分かるんじゃないの?

それは2次方程式のとき!他の方程式ではどう考えるかを説明していくよ!
「方程式の解」を、「グラフでの共有点」と考えることができました。
例えば、「方程式 \(x^2-4\) \(=\) \(0\) の解」は、「\(y=x^2-4\) と \(y=0\) の共有点」と考えることができます。
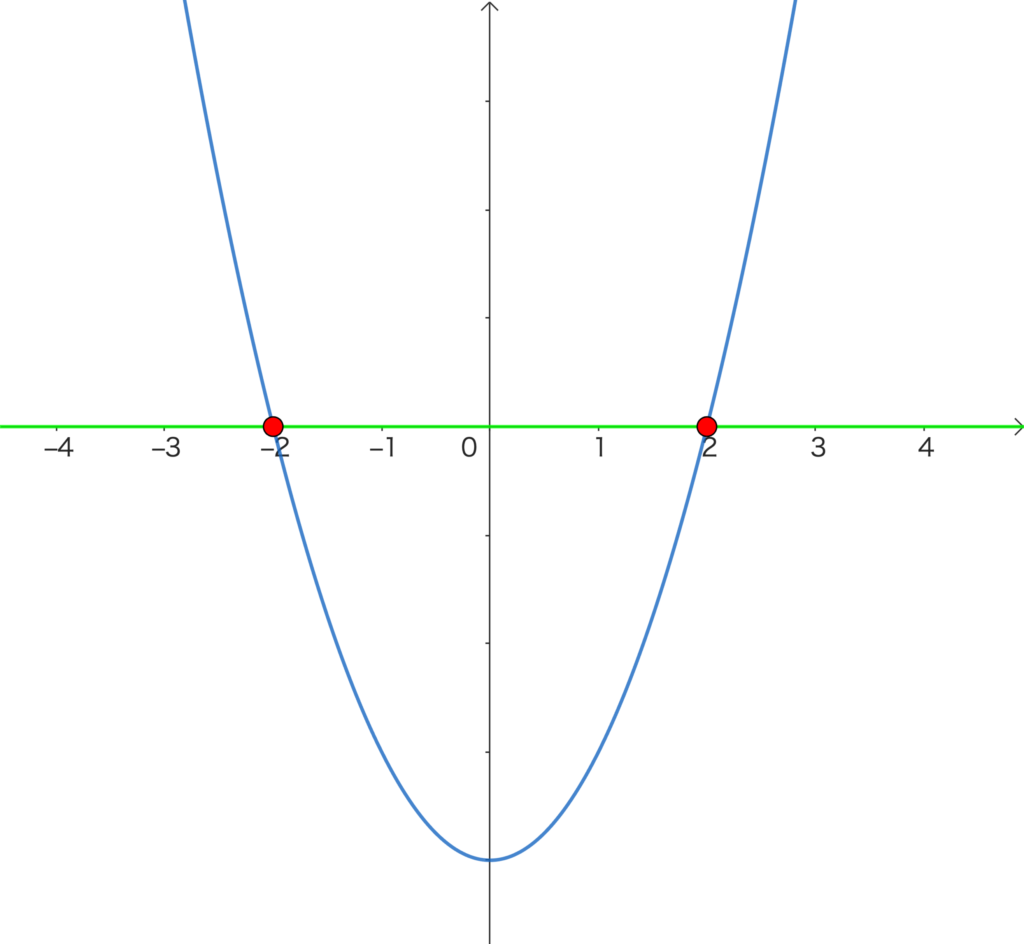
この考えを使って、次の例題を解いていきます。
\(a\) は定数とする。方程式 \(\frac{e^x}{x}=a\) の実数解の個数を求めよ。
「方程式 \(\frac{e^x}{x}\) \(=\) \(a\) の解」を、「\(y=\frac{e^x}{x}\) と \(y=a\) の共有点」と考えていきます。

\(y=\frac{e^x}{x}\) のグラフ•••。ちゃんとかけるかな?

微分法の応用11:「グラフのかき方」や微分法の応用12:「漸近線の種類」を復習しておこう!
まずは、\(y=\frac{e^x}{x}\) のグラフを考えます。
グラフは次の5つの流れでかいていきます。
- 定義域を確認する
- 微分計算により \(y’\) や \(y^{\prime\prime}\) を計算する
- \(y’=0\)、 \(y^{\prime\prime} = 0\) を求め増減表を作る
- 漸近線があれば図示する
- グラフをかく
1. 定義域の確認
\(f(x)=\frac{e^x}{x}\) とすると 定義域は \(x\neq0\)
2. \(y’\)を計算する
\(f'(x)=\frac{xe^x-e^x}{x^2}=\frac{(x-1)e^x}{x^2}\)
3. \(y’=0\)を計算し増減表を作る
\(f'(x)=0\) とすると \(x=1\)
4. 漸近線があれば図示する

漸近線は次の3つだったね。
- \(y = a\) 型の横の漸近線
- \(x = a\) 型の縦の漸近線
- \(y = ax + b\) 型の斜めの漸近線
「\(y = a\) 型の横の漸近線」は 関数の左右の端がどうなるかを調べるのでした。

関数の発散速度「\(\log{x}<<x^n<<a^x\)」で比べよう!
\(\displaystyle\lim_{n \to \infty} \frac{e^x}{x}= \infty\)
\(\displaystyle\lim_{n \to -\infty} \frac{e^x}{x} = 0\)
これにより、右端は \(\infty\) に発散し、左端は \(0\) に近づくことがわかりました。
「\(x = a\) 型の縦の漸近線」は関数の定義域の端を調べるのでした。
\(\displaystyle\lim_{n \to +0} \frac{e^x}{x} = \infty\)
\(\displaystyle\lim_{n \to -0} \frac{e^x}{x} = -\infty\)
これにより、\(x=0\) が漸近線であることがわかりました。
「\(y = ax + b\) 型の斜めの漸近線」は、「(1次式)+(分数関数)」でないため存在しません。
5. グラフをかく
1〜4の結果から、グラフは下図のグラフがかけます。
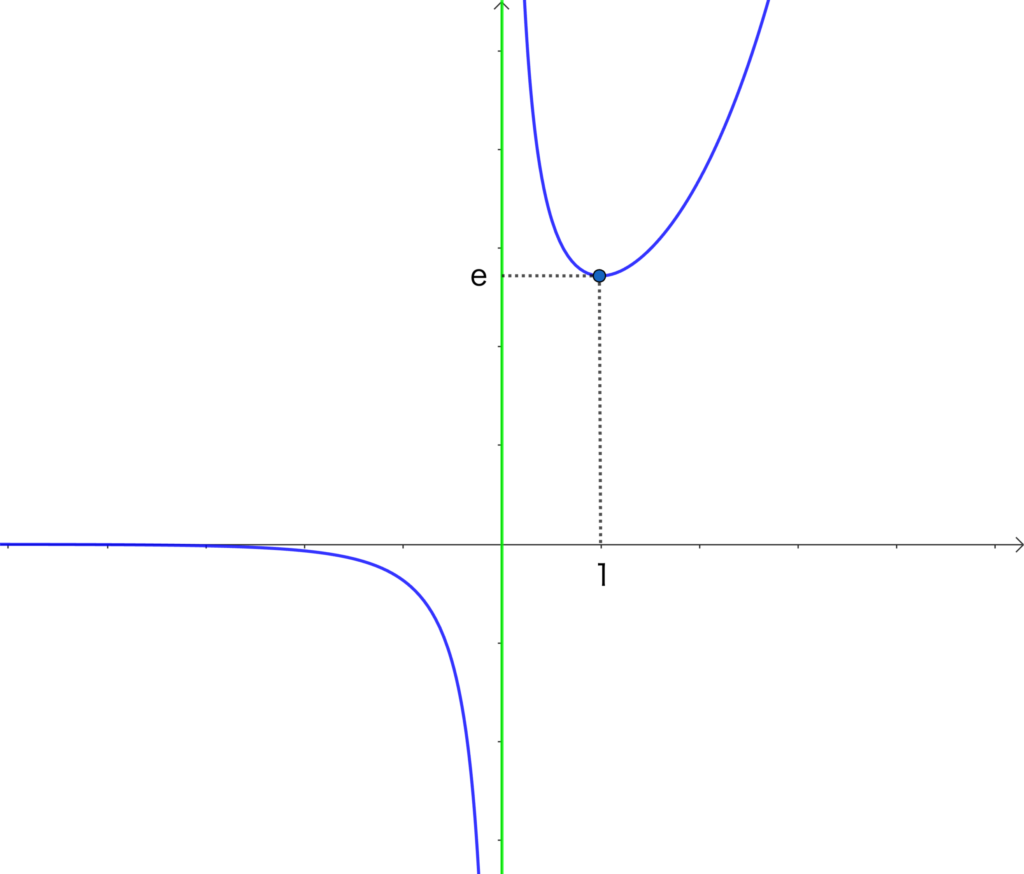

そうだった、そうだった。

次は \(y = a\) のグラフを考を考えよう!
あとは、\(y = a\) のグラフを考え、\(y=\frac{e^x}{x}\) との交点の個数を数えていきます。
\(y = a\) は \(x\) 軸に並行な直線ですから、
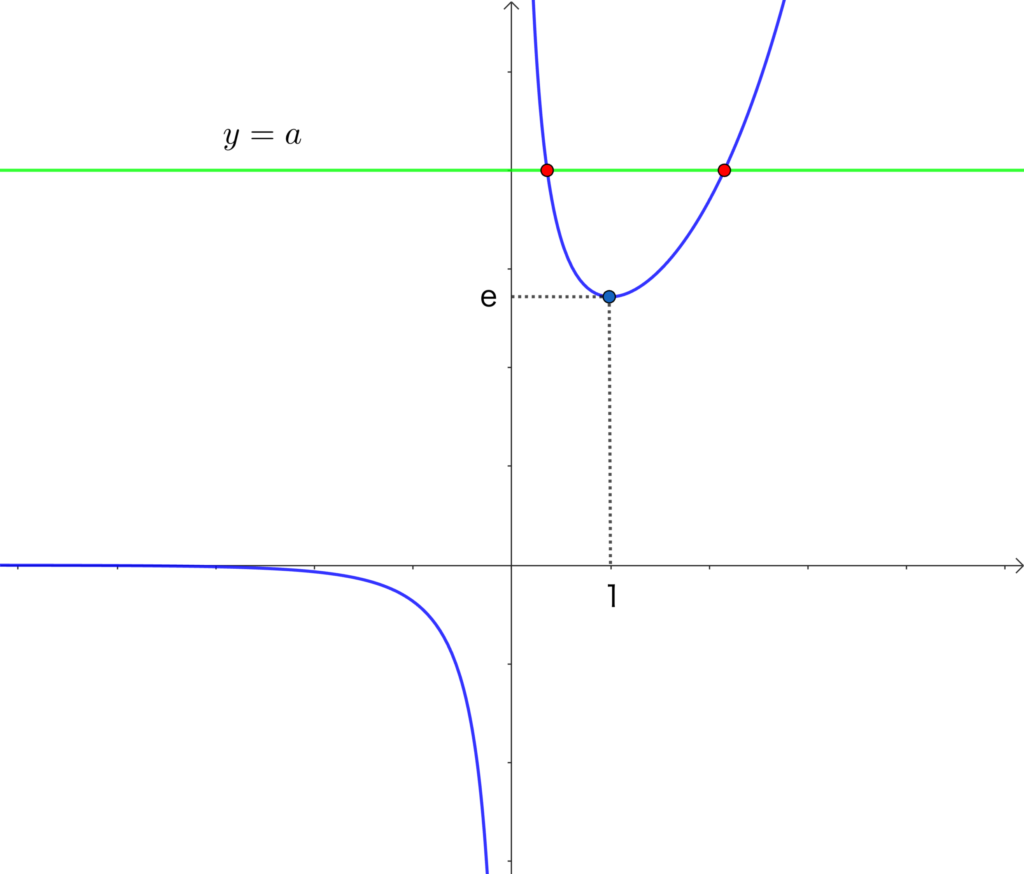
グラフより
\(a>e\) のとき \(2\) 個
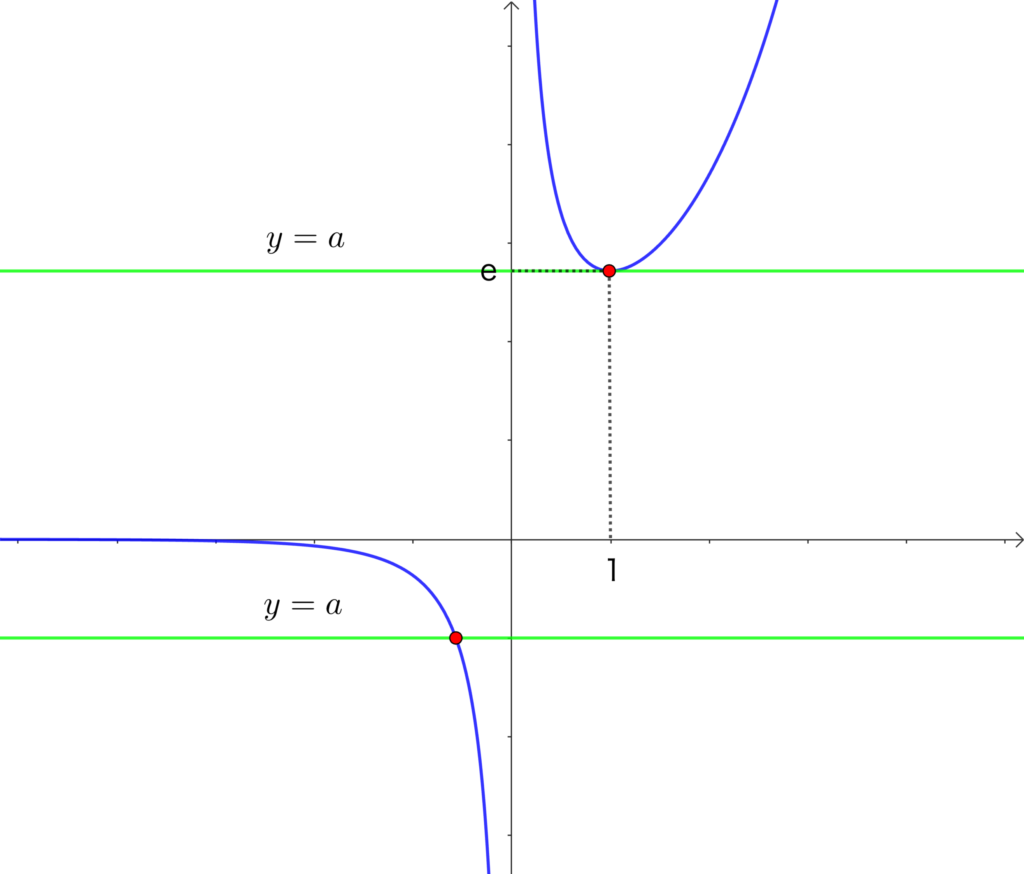
\(a=e,\) \(a<0\) のとき \(1\) 個
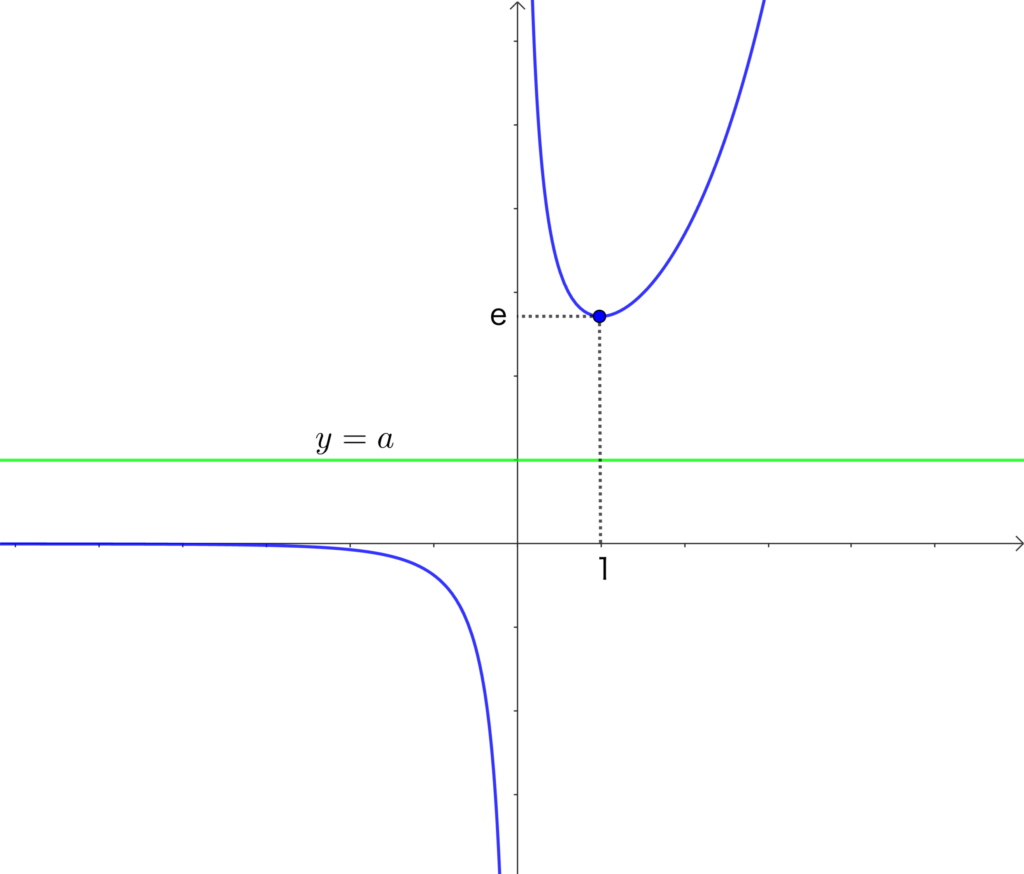
\(0≦a<e\) のとき \(0\) 個

定数 \(a\) だけが右辺にある状態のことを「定数分離」っていうよ。

「定数分離」ができるときは、この考え方でやるんだね!
\(a\) は定数とする。方程式 \(\frac{e^x}{x}=a\) の実数解の個数を求めよ。
\(f(x)=\frac{e^x}{x}\) とすると 定義域は \(x\neq0\)
\(f'(x)=\frac{xe^x-e^x}{x^2}=\frac{(x-1)e^x}{x^2}\)
\(f'(x)=0\) とすると \(x=1\)
\(\displaystyle\lim_{n \to \infty} f(x) = \infty\)
\(\displaystyle\lim_{n \to -\infty} f(x) = 0\)
\(\displaystyle\lim_{n \to +0} f(x) = \infty\)
\(\displaystyle\lim_{n \to -0} f(x) = -\infty\)
グラフより
\(a>e\) のとき \(2\) 個
\(a=e,\) \(a<0\) のとき \(1\) 個
\(0≦a<e\) のとき \(0\) 個
まとめ
今回の内容をしっかり整理しておこう!

グラフのいい練習になったな。
- 方程式 \(f(x) = g(x)\) の実数解の個数は、グラフ y = f(x) と y = g(x) の共有点の個数で求められる。
- 定数 \(a\) だけを右辺に分離するこの方法は「定数分離」と呼ばる。

最初に戻って、教科書の説明を読んでみよう!スラスラ理解できるはずだよ!





コメント