
今日の板書はこれ!
水平線を基準にして上を見上げるときの角度のこと。
水平線を基準にして下を見下ろすときの角度のこと。
\(\color{red}{\sin{\theta}}=\frac{\color{lime}{y}}{\color{hotpink}{r}}\) より \(\color{lime}{y}=\color{hotpink}{r}\color{red}{\sin{\theta}}\)
\(\color{red}{\cos{\theta}}=\frac{\color{deepskyblue}{x}}{\color{hotpink}{r}}\) より \(\color{deepskyblue}{x}=\color{hotpink}{r}\color{red}{\cos{\theta}}\)
\(\color{red}{\tan{\theta}}=\frac{\color{lime}{y}}{\color{deepskyblue}{x}}\) より \(\color{lime}{y}=\color{deepskyblue}{x}\color{red}{\tan{\theta}}\)

詳しく願いします!!
「人より勉強に時間がかかる」と感じていませんか?
私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。
• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」
• 「解答の意味が理解できず、勉強が進まない」
教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。
でも大丈夫!
このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。
「噛み砕き方」がわかれば、文章はぐっと読みやすくなります!
仰角・俯角とは?例題で分かりやすく解説!

今回は文章問題にチャレンジしていこう!
木の根元から水平に10m離れた地点に立って木の先端を見上げると、水平面となす角が21°であった。目の高さを1.6mとして、木の高さを求めよ。ただし、小数第2位を四捨五入せよ。
簡単な図を書くとこんな感じです。
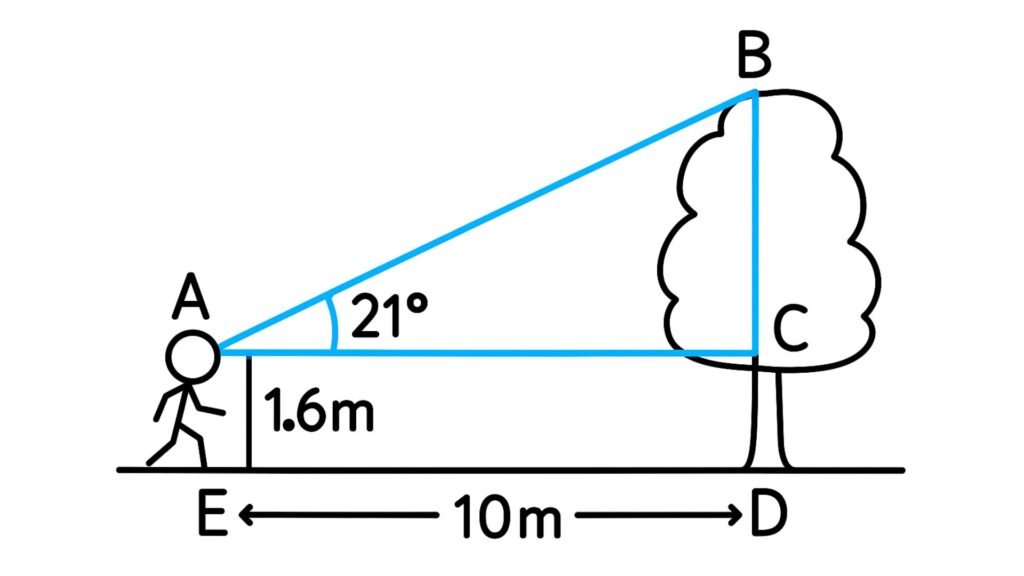
上図のようにA, B, C, D, E を定める。
仰角と俯角
今回の例題のように、「上を見上げたときの角度」を「仰角」と言います。
また、「下を見下げたときの角度」を「俯角」と言います。
水平線を基準にして上を見上げるときの角度のこと。
水平線を基準にして下を見下ろすときの角度のこと。
例題にチャレンジ
三角比を用いて、例題を解いていきます。
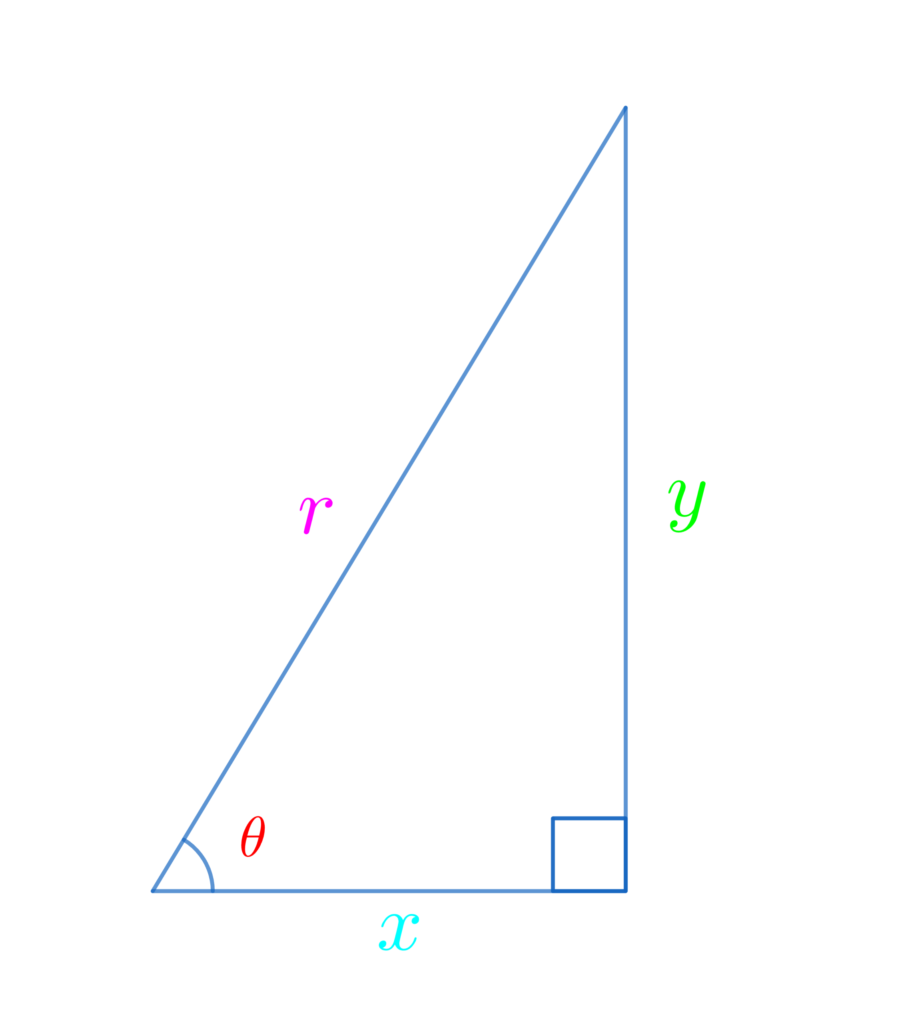
\(\displaystyle\color{red}{\cos{\theta}}=\frac{\color{deepskyblue}{底辺}}{\color{hotpink}{斜辺}}=\frac{\color{deepskyblue}{x}}{\color{hotpink}{r}}\)
\(\displaystyle\color{red}{\cos{\theta}}=\frac{\color{deepskyblue}{底辺}}{\color{hotpink}{斜辺}}=\frac{\color{deepskyblue}{x}}{\color{hotpink}{r}}\)
\(\displaystyle\color{red}{\tan{\theta}}=\frac{\color{lime}{対辺}}{\color{deepskyblue}{底辺}}=\frac{\color{lime}{y}}{\color{deepskyblue}{x}}\)

もう流石に覚えたた!
これらの式は、「三角比」と「2辺」の式です。
「三角比」は「2辺」から求めることができました。
この定義の式を変形させることで、「1辺」と「三角比」から「他の1辺」を求めることができるんです。

三角比の式を変形させてみよう!
\(\color{red}{\sin{\theta}}=\frac{\color{lime}{y}}{\color{hotpink}{r}}\) より \(\color{lime}{y}=\color{hotpink}{r}\color{red}{\sin{\theta}}\)
直角三角形の「斜辺」と「\(\sin{\theta}\)」から「高さ」を
\(\color{red}{\cos{\theta}}=\frac{\color{deepskyblue}{x}}{\color{hotpink}{r}}\) より \(\color{deepskyblue}{x}=\color{hotpink}{r}\color{red}{\cos{\theta}}\)
直角三角形の「斜辺」と「\(\cos{\theta}\)」から「底辺」を
\(\color{red}{\tan{\theta}}=\frac{\color{lime}{y}}{\color{deepskyblue}{x}}\) より \(\color{lime}{y}=\color{deepskyblue}{x}\color{red}{\tan{\theta}}\)
直角三角形の「底辺」と「\(\tan{\theta}\)」から「高さ」を求めることができます。
もう1度例題を見てみましょう。
木の根元から水平に10m離れた地点に立って木の先端を見上げると、水平面となす角が21°であった。目の高さを1.6mとして、木の高さを求めよ。ただし、小数第2位を四捨五入せよ。

木の高さBDは、BC+1.6ですから、BCが分かれば、木の高さを求められます。
ここで、水色の直角三角形に注目します。
BCは、この直角三角形の「高さ」のことです。
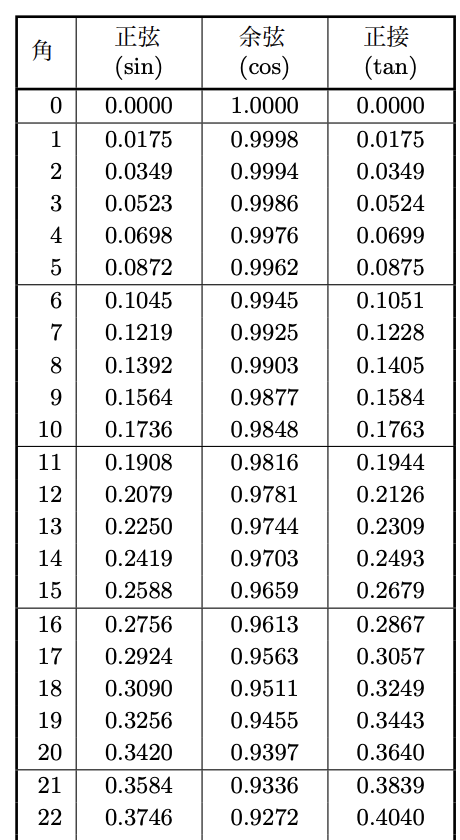
また、「底辺AC」は 10m であり「三角比」は 三角比の表 から求めることができるので、
\(\color{lime}{y}=\color{deepskyblue}{x}\color{red}{\tan{\theta}}\) を使えば、BCを求められますね。
木の高さBDは、BC+1.6でした。
これで、木の高さを求めることができました!
まとめ:三角比による計測

さて、今回のまとめだよ!
三角比の定義から、「辺の長さ」を求めることができます!
水平線を基準にして上を見上げるときの角度のこと。
水平線を基準にして下を見下ろすときの角度のこと。
\(\color{red}{\sin{\theta}}=\frac{\color{lime}{y}}{\color{hotpink}{r}}\) より \(\color{lime}{y}=\color{hotpink}{r}\color{red}{\sin{\theta}}\)
\(\color{red}{\cos{\theta}}=\frac{\color{deepskyblue}{x}}{\color{hotpink}{r}}\) より \(\color{deepskyblue}{x}=\color{hotpink}{r}\color{red}{\cos{\theta}}\)
\(\color{red}{\tan{\theta}}=\frac{\color{lime}{y}}{\color{deepskyblue}{x}}\) より \(\color{lime}{y}=\color{deepskyblue}{x}\color{red}{\cos{\theta}}\)

また一つ賢くなった!






コメント