
今日の板書はこれ!
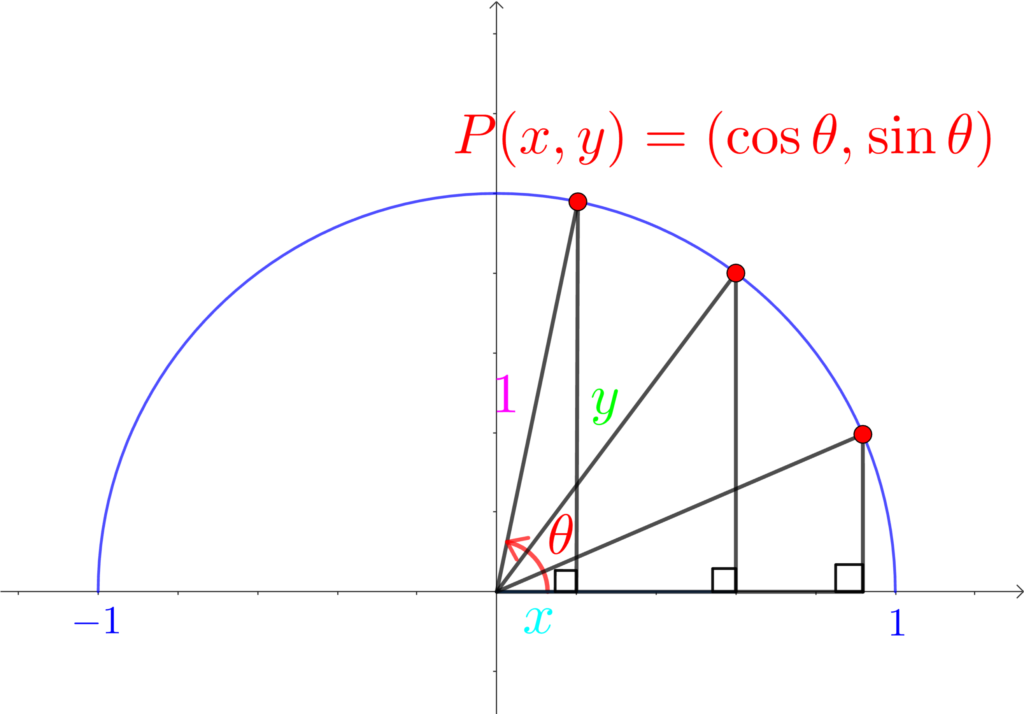
長さ\(1\)、\(x\) 軸方向からの回転角 \(\theta\) の線分と単位円の交点 \(P\) の座標が \((\cos{\theta}, \sin{\theta})\)
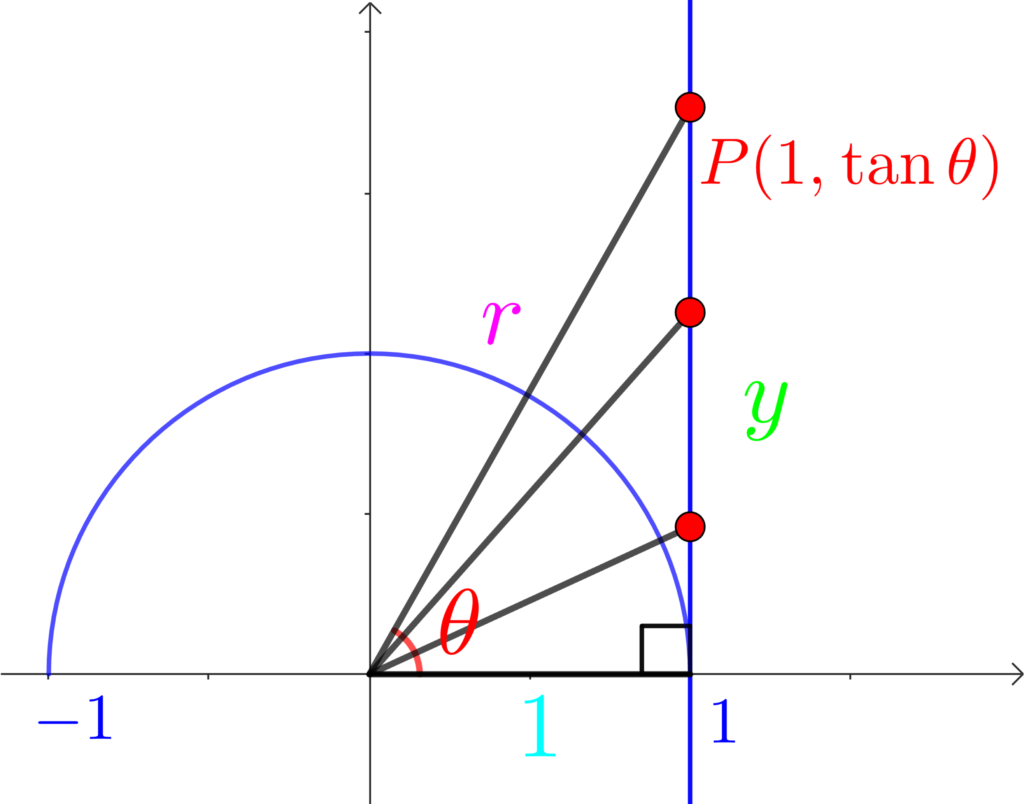
\(x\) 軸方向からの回転角 \(\theta\) の直線と直線 \(x=1\) との交点 \(P\) の\(y\) 座標が \(\tan{\theta}\)
- 90°関連(0°, 90°, 180°)の三角比
→ 単位円で考える。(\(\sin{\theta}\) は \(y\) 座標、\(\cos{\theta}\)は \(x\) 座標 )
- 30°関連(30°, 60°, 120°, 150°)の三角比
→ 大きさは \(\frac{1}{2}=0.5\) or \(\frac{\sqrt{3}}{2}≒0.9\) 。符号は単位円で考える。
- 45°関連(45°, 135°)の三角比
→ 大きさは \(\frac{1}{\sqrt{2}}\) 。符号は単位円で考える。
- 90°関連(0°, 90°, 180°)の三角比
→ 単位円で考える。(\(\tan{\theta}\) は \(x=1\)の\(y\) 座標)
- 30°関連(30°, 60°, 120°, 150°)の三角比
→ 大きさは \(\frac{1}{\sqrt{3}}≒0.6\) or \(\sqrt{3}≒1.7\) 。符号は単位円で考える。
- 45°関連(45°, 135°)の三角比
→ 大きさは \(1\) 。符号は単位円で考える。

詳しく願いします!!
「人より勉強に時間がかかる」と感じていませんか?
私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。
• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」
• 「解答の意味が理解できず、勉強が進まない」
教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。
でも大丈夫!
このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。
「噛み砕き方」がわかれば、文章はぐっと読みやすくなります!
単位円を用いた三角比の定義

単位円を使って三角比の定義し直そう!

そもそも単位円ってなんだっけ?
単位円とは、半径が1の円のことです。
数Ⅰでは、上半分の単位円しか使いません。
復習ですが、直角三角形を使った三角比の定義はこんな感じでしたね。
さすがに覚えられましたか?
\(\displaystyle\color{red}{\cos{\theta}}=\frac{\color{deepskyblue}{底辺}}{\color{hotpink}{斜辺}}=\frac{\color{deepskyblue}{x}}{\color{hotpink}{r}}\)
\(\displaystyle\color{red}{\cos{\theta}}=\frac{\color{deepskyblue}{底辺}}{\color{hotpink}{斜辺}}=\frac{\color{deepskyblue}{x}}{\color{hotpink}{r}}\)
\(\displaystyle\color{red}{\tan{\theta}}=\frac{\color{lime}{対辺}}{\color{deepskyblue}{底辺}}=\frac{\color{lime}{y}}{\color{deepskyblue}{x}}\)
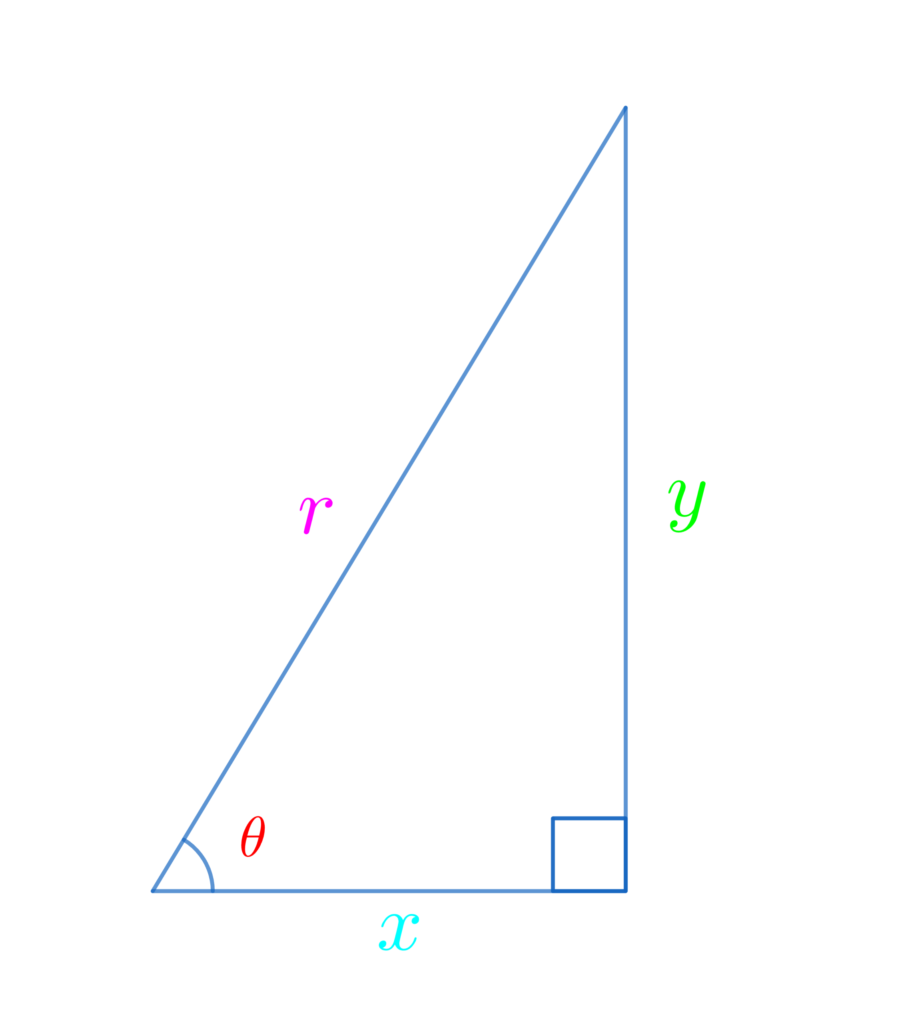
単位円を使って三角比を定義し直すと、0°から90°までだった三角比が、180°まで考えられるようになるんです!
単位円を使った \(\sin\) の定義
まずは、\(\sin\) を単位円を使って定義していきます。
次の単位円を見てください。
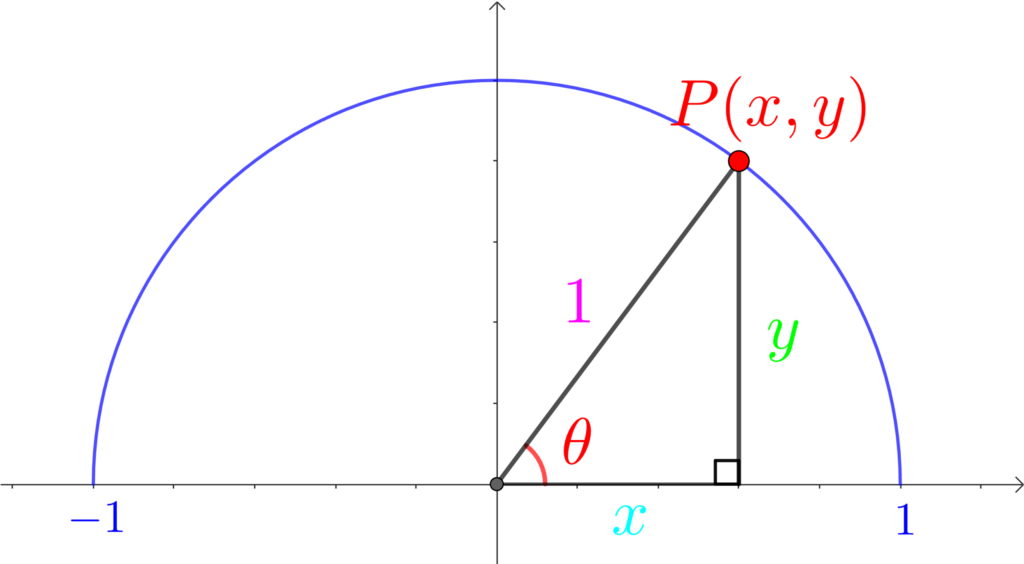
単位円上に点P \((x, y)\) を作り、点Pを頂点にもつ、直角三角形を作りました。
単位円は「半径が1の円」ですから、この直角三角形の斜辺は1になります。
そして、\(\displaystyle\color{red}{\sin{\theta}}=\frac{\color{lime}{対辺}}{\color{hotpink}{斜辺}}=\frac{\color{lime}{y}}{\color{hotpink}{r}}\) でしたから、
\(\displaystyle\color{red}{\sin{\theta}}=\frac{\color{lime}{対辺}}{\color{hotpink}{斜辺}}=\frac{\color{lime}{y}}{\color{hotpink}{1}}=\color{lime}{y}\)
よって、\(\color{red}{\sin{\theta}}=\color{lime}{y}\) となります。
つまり、単位円での\(\sin{\theta}\) は、点Pの \(y\) 座標 ってことです。
どうですか?
とってもシンプルに定義できて気持ちいいですよね。
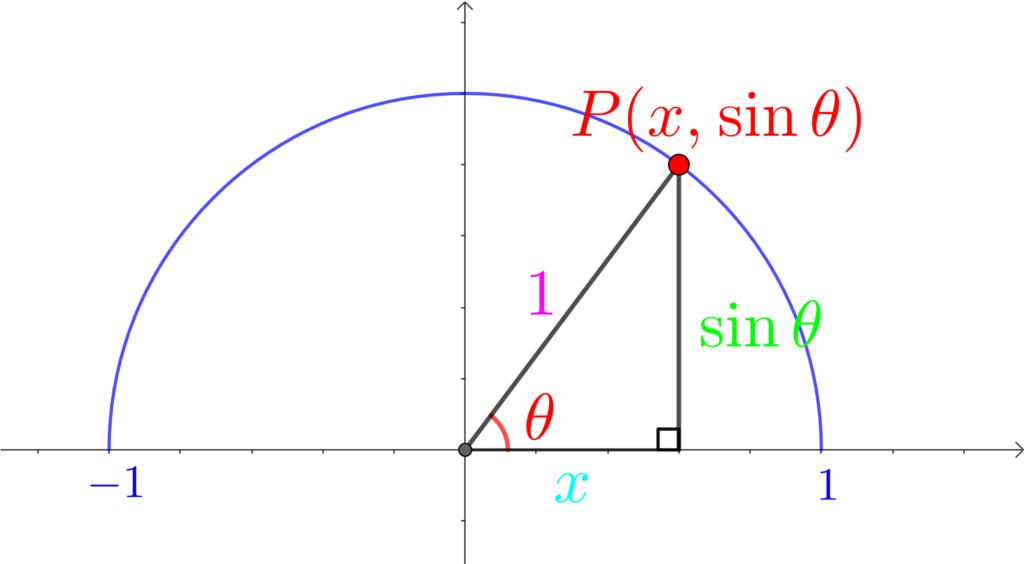

「\(\sin{\theta}\) は\(y\) 座標」って10回唱えよう!

\(\sin{\theta}\) は\(y\) 座標、\(\sin{\theta}\) は\(y\) 座標、\(\sin{\theta}\) は\(y\) 座標、・・・
単位円を使った \(\cos\) の定義
次に、\(\cos\) を単位円を使って定義していきます。

直角三角形での \(\cos\) の定義は \(\displaystyle\color{red}{\cos{\theta}}=\frac{\color{deepskyblue}{底辺}}{\color{hotpink}{斜辺}}=\frac{\color{deepskyblue}{x}}{\color{hotpink}{r}}\)
単位円での直角三角形の斜辺は1ですから、
\(\displaystyle\color{red}{\cos{\theta}}=\frac{\color{deepskyblue}{底辺}}{\color{hotpink}{斜辺}}=\frac{\color{deepskyblue}{x}}{\color{hotpink}{1}}=\color{deepskyblue}{x}\)
よって、\(\color{red}{\cos{\theta}}=\color{deepskyblue}{x}\) となります。
つまり、単位円での\(\cos{\theta}\) は、点Pの \(x\) 座標 ってことです。
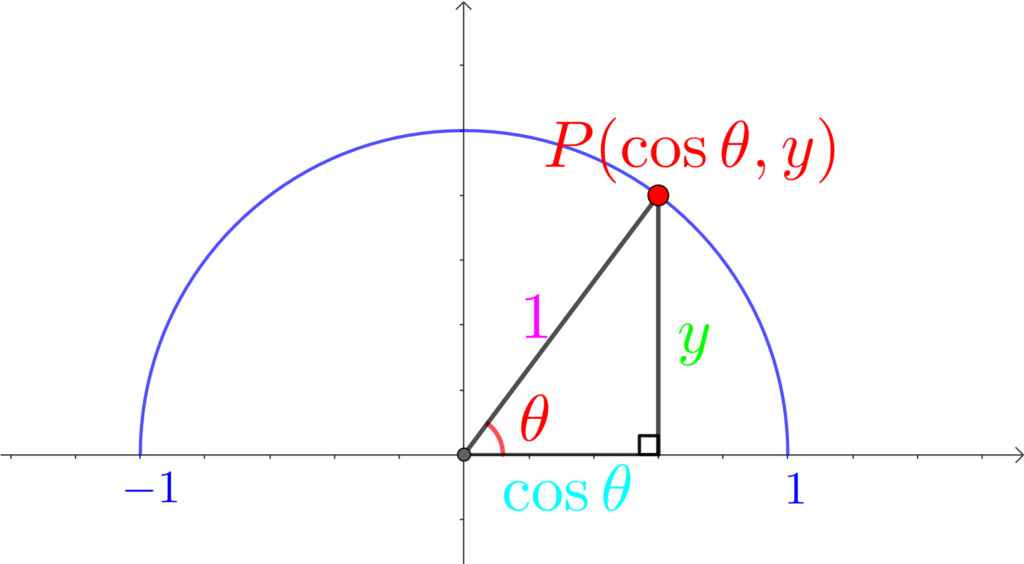

「\(\cos{\theta}\) は\(x\) 座標」って10回唱えよう!

\(\cos{\theta}\) は\(x\) 座標、\(\cos{\theta}\) は\(x\) 座標、\(\cos{\theta}\) は\(x\) 座標、・・・
単位円を使った \(\tan\) の定義
最後に\(\tan\) を単位円を使って定義していきます。
\(\sin\), \(\cos\) は「分母が1」になるような直角三角形で考えていました。
\(\displaystyle\color{red}{\tan{\theta}}=\frac{\color{lime}{対辺}}{\color{deepskyblue}{底辺}}=\frac{\color{lime}{y}}{\color{deepskyblue}{x}}\) ですから、「分母は \(x\) 」です。
\(\tan\) でも「分母が1」になるように考えたいので、 \(x\) が1になるような直角三角形で考えます。
それが、下の図の直角三角形です。
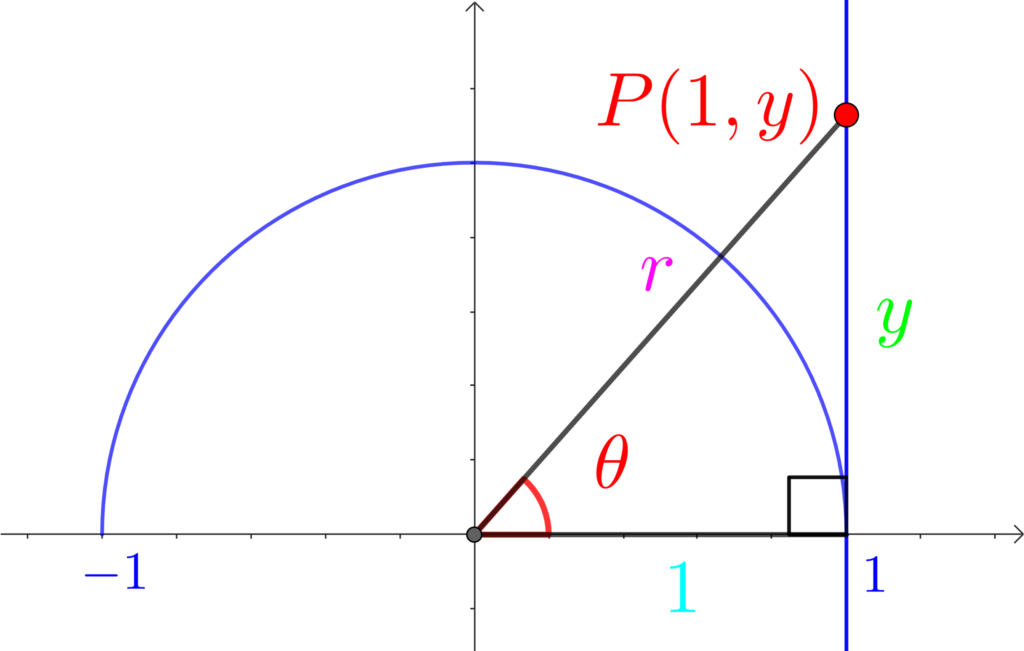
直線 \(x=1\) 上に点Pを作りました。
この直角三角形では、底辺が単位円の半径1になるため、
\(\displaystyle\color{red}{\tan{\theta}}=\frac{\color{lime}{対辺}}{\color{deepskyblue}{底辺}}=\frac{\color{lime}{y}}{\color{deepskyblue}{1}}=\color{lime}{y}\)
よって、\(\color{red}{\tan{\theta}}=\color{lime}{y}\)
つまり、直線 \(x=1\) との交点 \(P\) の\(y\) 座標が \(\tan{\theta}\)になります。
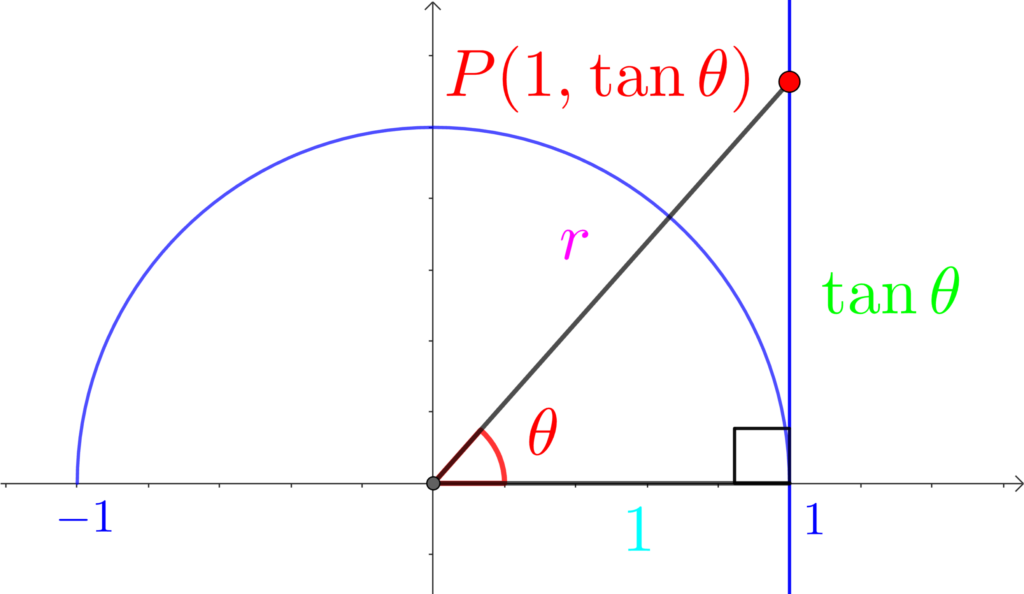

「\(\tan{\theta}\) は \(x=1\)の\(y\) 座標」って10回唱えよう!

\(\tan{\theta}\) は\(x=1\)の\(y\) 座標、\(\tan{\theta}\) は\(x=1\)の\(y\) 座標、\(\tan{\theta}\) は\(x=1\)の\(y\) 座標、・・・
単位円を使った定義で150°の三角比を考えてみよう!

10回ずつ唱えたから覚えられた?

んー、もう忘れた。
「\(\sin{\theta}\) は\(y\) 座標」、「\(\cos{\theta}\) は\(x\) 座標」、「\(\tan{\theta}\) は \(x=1\)の\(y\) 座標」でした。
練習として、150°の三角比 \(\sin{150°}\) \(\cos{150°}\) \(\tan{150°}\)を求めましょう。
下の単位円で、それぞれがどこの値なのかを確認してください。
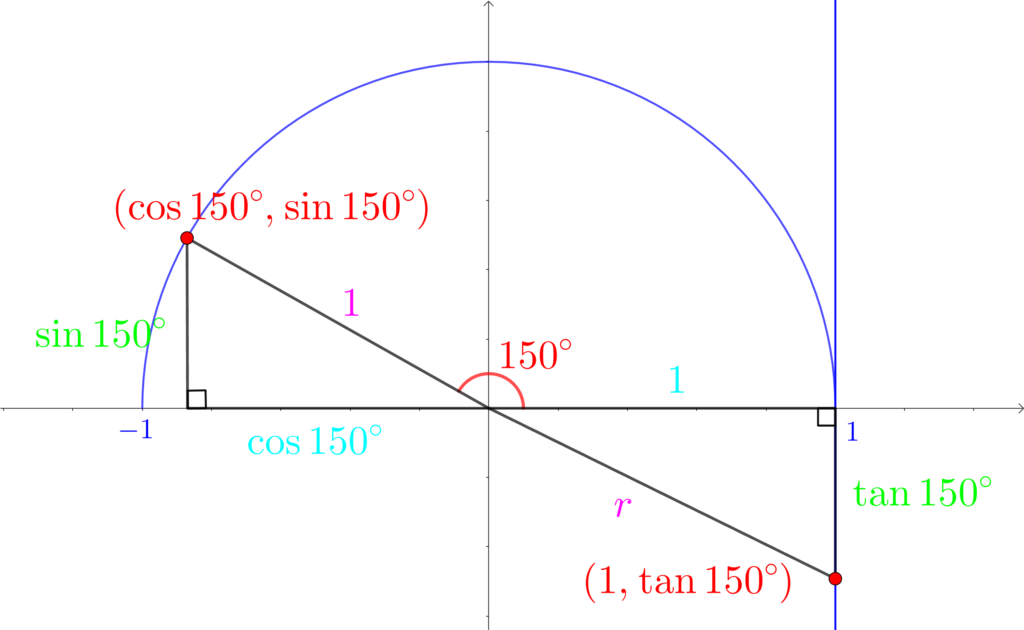
「\(\sin{150°}\) は\(y\) 座標」、「\(\cos{150°}\) は\(y\) 座標」、「\(\tan{150°}\) は \(x=1\)の\(y\) 座標」です。

この図の見方がわからない人は、もう一回上に戻って確認してみよう!
2つの直角三角形はどちらも「 \(30°,60°,90°\) 」の直角三角形です。
ですので、辺の比は「 \(1:2:\sqrt{3}\) 」ですから、
\(\displaystyle\sin{150°}=\frac{1}{2}\)
\(\displaystyle\cos{150°}=-\frac{\sqrt{3}}{2}\)
\(\displaystyle\tan{150°}=-\frac{1}{\sqrt{3}}\)

できたー!これで、単位円での定義完璧。
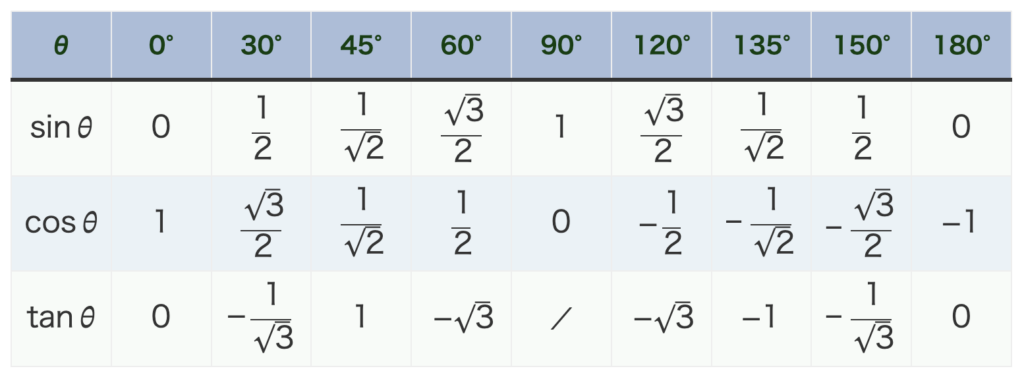
三角比の表

次の表を完成させれるかな?
0°から90°までだった三角比が、180°まで考えられるようになりました。
主要な三角比の値を自分で求められるようになりましょう!
| θ | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° |
|---|---|---|---|---|---|---|---|---|---|
| \(\sin{\theta}\) | |||||||||
| \(\cos{\theta}\) | |||||||||
| \(\tan{\theta}\) | / |

んー。頑張ってみる•••。
※ \(\tan{90°}\) は 直線 \(x=1\) との交点が存在せず、値をとらないため「/」を入れてあります。

三角比の表の暗記法

さっき作った三角比の表を、一瞬で考えられるようになろう!
毎回、単位円の直角三角形から辺の比を使って三角比を求めるのは、とても時間がかかります。
しかし、私は記憶力が乏しく、この表を全て暗記するのは難しい。
正しく暗記できずに、「テストで全滅」ってこともありえます。
そこで、全てを暗記するのではなく、「一部のみを暗記し、一部を考える」、ハイブリッドな覚え方をしています。
覚えていることはこれだけ。
30°関連(30°, 60°, 120°, 150°)
- \(\sin\), \(\cos\) → \(\frac{1}{2}=0.5\) or \(\frac{\sqrt{3}}{2}≒0.9\)
- \(\tan\) → \(\frac{1}{\sqrt{3}}≒0.6\) or \(\sqrt{3}≒1.7\)
45°関連(45°, 135°)
- \(\sin\), \(\cos\) → \(\frac{1}{\sqrt{2}}\)
- \(\tan\) → \(1\)
あとは、単位円で考える。
この暗記法を使って、もう1度150°の三角比を考えてみます。
まずは、単位円(1周)と150°を書きます。
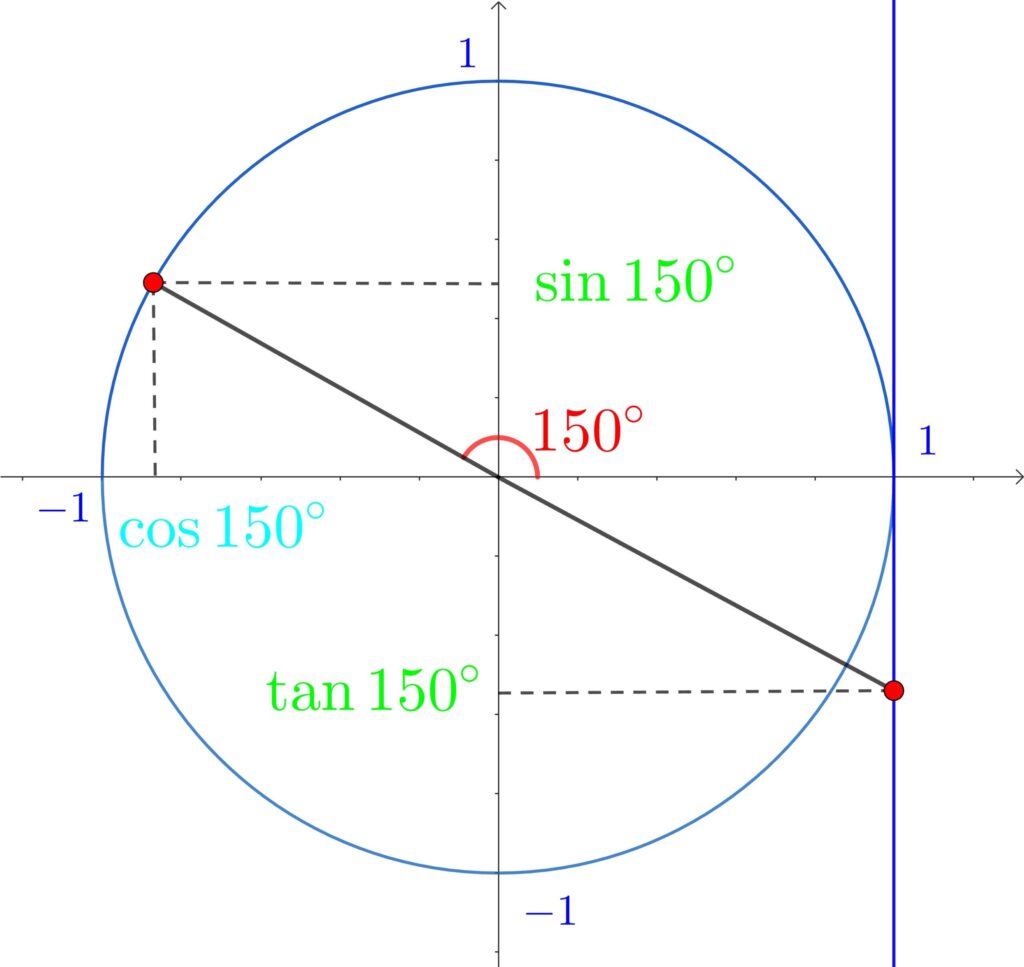
その後、この単位円を見ながら
\(\sin\) は \(y\) 座標だから、符号は「+」で、30°関連の大きさは、\(\frac{1}{2}=0.5\) or \(\frac{\sqrt{3}}{2}≒0.9\) だから、どっちかっていうと \(\frac{1}{2}\) だよな。
→ \(\displaystyle\sin{150°}=\frac{1}{2}\)
\(\cos\)は \(x\) 座標だから、符号は「ー」で、30°関連の大きさは、\(\frac{1}{2}=0.5\) or \(\frac{\sqrt{3}}{2}≒0.9\) だから、どっちかっていうと \(\frac{\sqrt{3}}{2}\) だよな。
→ \(\displaystyle\sin{\theta}=-\frac{\sqrt{3}}{2}\)
\(\tan\) は \(x=1\)の\(y\) 座標だから、符号は「ー」で、30°関連の大きさは、\(\frac{1}{\sqrt{3}}≒0.6\) or \(\sqrt{3}≒1.7\) だから、どっちかっていうと \(\frac{1}{\sqrt{3}}\) だよな。
→ \(\displaystyle\tan{\theta}=-\frac{1}{\sqrt{3}}\)
こんな感じで、暗記する部分と、考える部分に分けて、すぐに分かるようにしています。
慣れれば、頭の中の単位円で考えるので、実際に単位円も書く必要はありません。
ぜひ参考にして欲しいと思います。

この考え方でもう一回三角比の表作ってみよっかな。一緒にやらない?
- 90°関連(0°, 90°, 180°)の三角比
→ 単位円で考える。(\(\sin{\theta}\) は \(y\) 座標、\(\cos{\theta}\)は \(x\) 座標 )
- 30°関連(30°, 60°, 120°, 150°)の三角比
→ 大きさは \(\frac{1}{2}=0.5\) or \(\frac{\sqrt{3}}{2}≒0.9\) 。符号は単位円で考える。
- 45°関連(45°, 135°)の三角比
→ 大きさは \(\frac{1}{\sqrt{2}}\) 。符号は単位円で考える。
- 90°関連(0°, 90°, 180°)の三角比
→ 単位円で考える。(\(\tan{\theta}\) は \(x=1\)の\(y\) 座標)
- 30°関連(30°, 60°, 120°, 150°)の三角比
→ 大きさは \(\frac{1}{\sqrt{3}}≒0.6\) or \(\sqrt{3}≒1.7\) 。符号は単位円で考える。
- 45°関連(45°, 135°)の三角比
→ 大きさは \(1\) 。符号は単位円で考える。
まとめ:単位円を用いた三角比の定義

さて、今回のまとめだよ!
三角比を単位円を使って定義し直しました。
とってもシンプルに定義することができましたね。
長さ\(1\)、\(x\) 軸方向からの回転角 \(\theta\) の線分と単位円の交点 \(P\) の座標が \((\cos{\theta}, \sin{\theta})\)

\(x\) 軸方向からの回転角 \(\theta\) の直線と直線 \(x=1\) との交点 \(P\) の\(y\) 座標が \(\tan{\theta}\)


- 90°関連(0°, 90°, 180°)の三角比
→ 単位円で考える。(\(\sin{\theta}\) は \(y\) 座標、\(\cos{\theta}\)は \(x\) 座標 )
- 30°関連(30°, 60°, 120°, 150°)の三角比
→ 大きさは \(\frac{1}{2}=0.5\) or \(\frac{\sqrt{3}}{2}≒0.9\) 。符号は単位円で考える。
- 45°関連(45°, 135°)の三角比
→ 大きさは \(\frac{1}{\sqrt{2}}\) 。符号は単位円で考える。
- 90°関連(0°, 90°, 180°)の三角比
→ 単位円で考える。(\(\tan{\theta}\) は \(x=1\)の\(y\) 座標)
- 30°関連(30°, 60°, 120°, 150°)の三角比
→ 大きさは \(\frac{1}{\sqrt{3}}≒0.6\) or \(\sqrt{3}≒1.7\) 。符号は単位円で考える。
- 45°関連(45°, 135°)の三角比
→ 大きさは \(1\) 。符号は単位円で考える。

また一つ賢くなった!






コメント