
今日の板書はこれ!
直線 \(y=mx\) と \(x\) 軸の正の向きとのなす角 \(\theta\) とすると \(m=\tan{\theta}\)
直線 \(y=\sqrt{3}x\) と \(x\) 軸の正の向きとのなす角 \(\theta\) を求めよ。
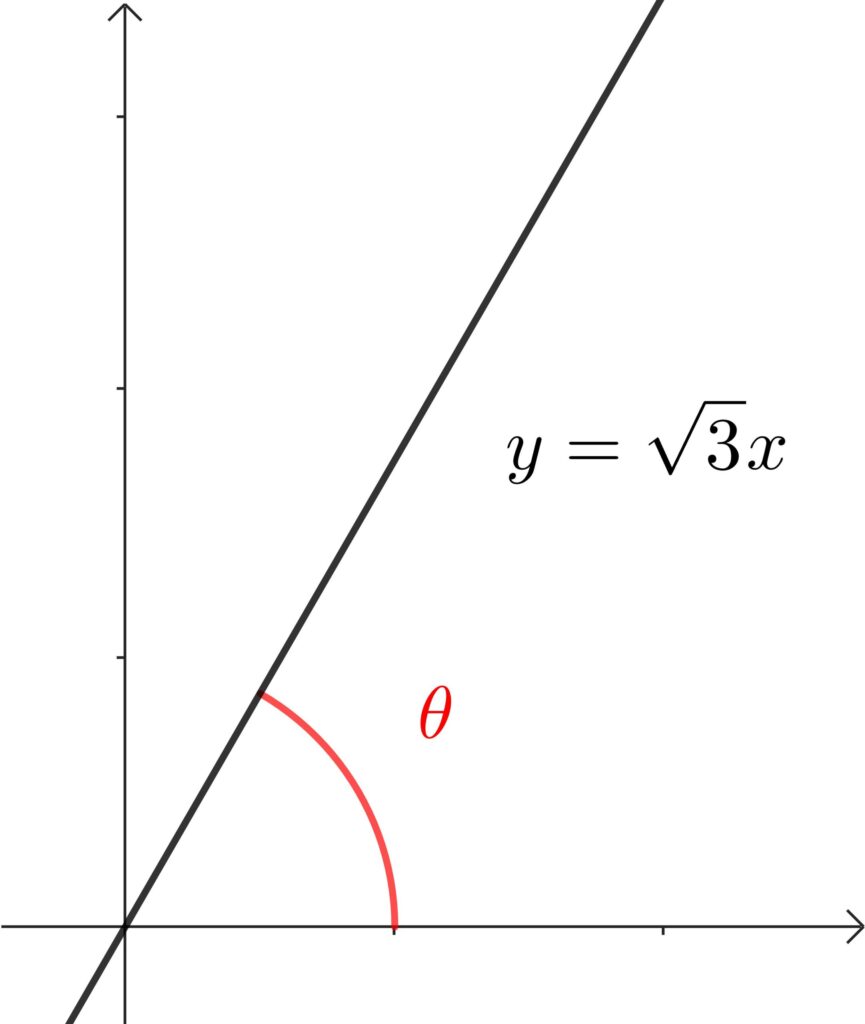
\(\tan{\theta}=\sqrt{3}\) より \(\theta=60°\)

もっと詳しく願いします!!
「人より勉強に時間がかかる」と感じていませんか?
私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。
• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」
• 「解答の意味が理解できず、勉強が進まない」
教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。
でも大丈夫!
このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。
「噛み砕き方」がわかれば、文章はぐっと読みやすくなります!
直線の傾きとtanθ

今回はこの例題に挑戦するよ!
直線 \(y=\sqrt{3}x\) と \(x\) 軸の正の向きとのなす角 \(\theta\) を求めよ。

どうやって解くの?
「傾きは \(\tan{\theta}\) 」なので \(\tan{\theta}=\sqrt{3}\) より \(\theta=60°\) です。

なぜ!?
\(\tan{\theta}=\sqrt{3}\) から \(\theta=60°\) を導けない人は下を参考にしてみてね↓
なぜ、傾きがtanθ?
\(\tan{\theta}\) は、図形的には「回転角 \(\theta\) の直線と直線 \(x=1\) との交点の \(y\) 座標のことでした。
\(x\) 軸方向からの回転角 \(\theta\) の直線と直線 \(x=1\) との交点 \(P\) の\(y\) 座標が \(\tan{\theta}\)
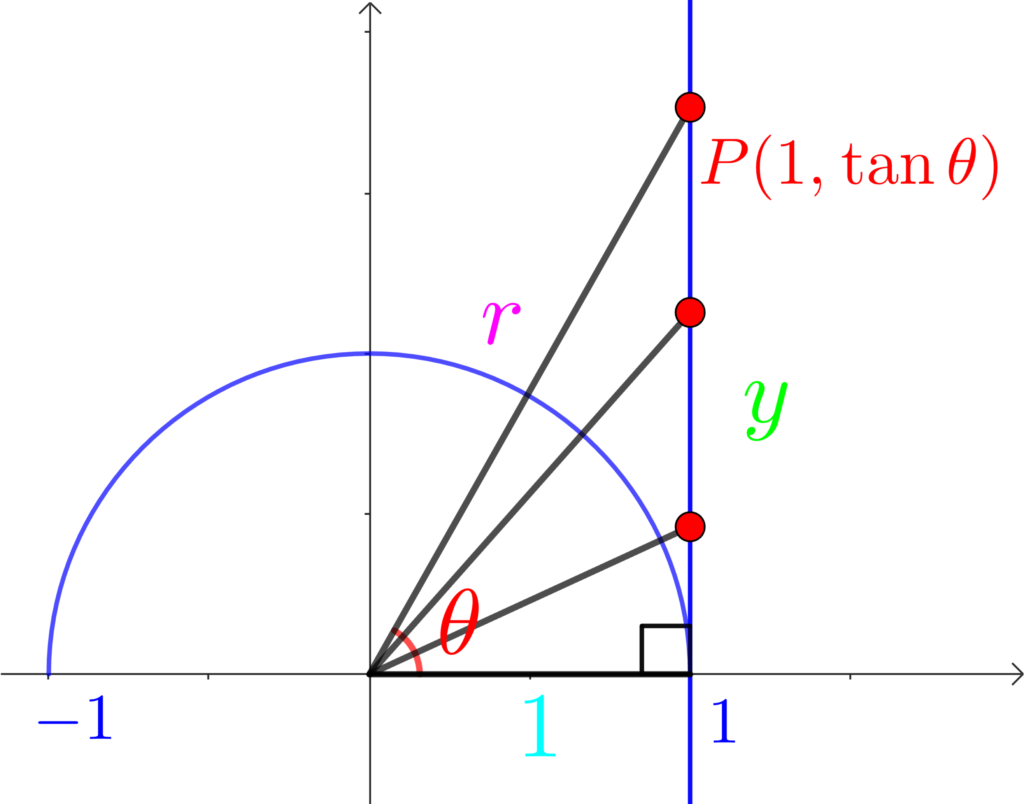
そして、直線の傾きは \(\displaystyle\frac{yの増加量}{xの増加量}\) でした。
ですから、回転角 \(\theta\) の直線の直線の傾きは、\(x\) 方向に1進むとき、\(y\) 方向に \(\tan{\theta}\) 進むので、
\(\color{red}{\text{直線の傾き}}=\displaystyle\frac{yの増加量}{xの増加量} =\frac{\tan{\theta}}{1}=\color{red}{\tan{\theta}}\)
つまり、直線の「傾きが \(\tan{\theta}\)」になるんです。

おー!ほんとだ!「傾きは \(\tan{\theta}\) !」
まとめ:直線の傾きとtanθ

さて、今回のまとめだよ!
直線の傾きとtanθの関係について勉強しました。
直線 \(y=mx\) と \(x\) 軸の正の向きとのなす角 \(\theta\) とすると \(m=\tan{\theta}\)
直線 \(y=\sqrt{3}x\) と \(x\) 軸の正の向きとのなす角 \(\theta\) を求めよ。

\(\tan{\theta}=\sqrt{3}\) より \(\theta=60°\)

また一つ賢くなった!








コメント