
今日の板書はこれ!
① sin と cos と tan の関係式:\(\displaystyle\tan{\theta}=\frac{\sin{\theta}}{\cos{\theta}}\)
② sin と cos の関係式:\(\sin{^2}\theta+\cos{^2}\theta=1\)
③ cos と tan の関係性:\(\displaystyle 1+\tan{^2}\theta=\frac{1}{\cos{^2}\theta}\)
\(\theta\) は鋭角とする。\(\color{deepskyblue}{\sin\theta=\frac{2}{3}}\) のとき、\(\color{lime}{\cos\theta}\) と \(\color{hotpink}{\tan\theta}\) の値を求めよ。
\(\cos\theta>0\) より

もっと詳しく願いします!!
「人より勉強に時間がかかる」と感じていませんか?
私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。
• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」
• 「解答の意味が理解できず、勉強が進まない」
教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。
でも大丈夫!
このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。
「噛み砕き方」がわかれば、文章はぐっと読みやすくなります!
三角比の相互関係とは?

今回は、sin, cos, tanの関係について学んでいくよ!

三角比の関係?
\(\sin\) と \(\cos\) と \(\tan\) は、お互いに関係し合っています。
その関係性を使うと、1つの三角比から、他の2つを求めることができるようになります。
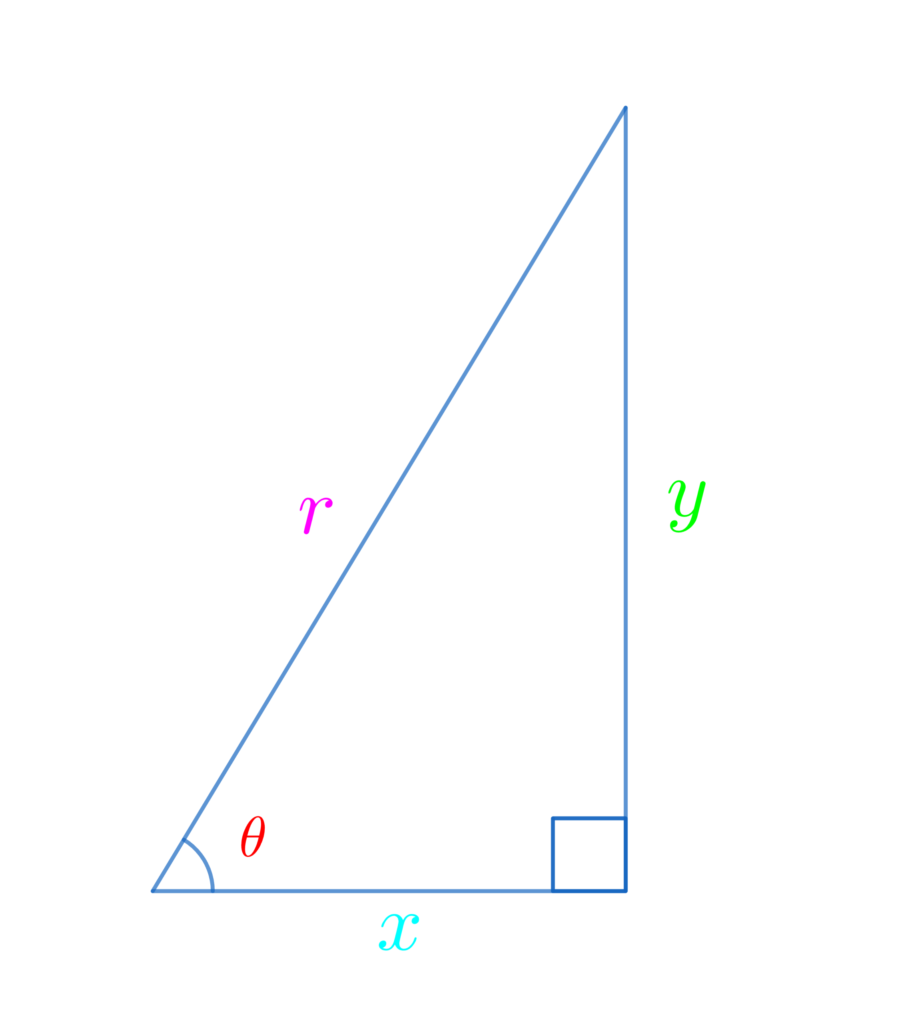
まずは、直角三角形の定義を復習しましょう。
\(\displaystyle\color{red}{\sin{\theta}}=\frac{\color{lime}{対辺}}{\color{hotpink}{斜辺}}=\frac{\color{lime}{y}}{\color{hotpink}{r}}\) より \(\color{lime}{y}=\color{hotpink}{r}\color{red}{\sin{\theta}}\)
\(\displaystyle\color{red}{\cos{\theta}}=\frac{\color{deepskyblue}{底辺}}{\color{hotpink}{斜辺}}=\frac{\color{deepskyblue}{x}}{\color{hotpink}{r}}\) より \(\color{deepskyblue}{x}=\color{hotpink}{r}\color{red}{\cos{\theta}}\)
\(\displaystyle\color{red}{\tan{\theta}}=\frac{\color{lime}{対辺}}{\color{deepskyblue}{底辺}}=\frac{\color{lime}{y}}{\color{deepskyblue}{x}}\) より \(\color{lime}{y}=\color{deepskyblue}{x}\color{red}{\tan{\theta}}\)
sinとcosとtanの関係

まずは、sinとcosとtanの関係について学んでいこう!
sinとcosとtanの間には、次のような関係が成り立ちます。
\(\displaystyle\tan{\theta}=\frac{\sin{\theta}}{\cos{\theta}}\)
なぜ成り立つのか、理由を分かりやすく解説
\(\displaystyle\tan{\theta}=\frac{\color{lime}{y}}{\color{deepskyblue}{x}}\) でした。
そして、\(\color{lime}{y}=\color{hotpink}{r}\sin{\theta}\)、\(\color{deepskyblue}{x}=\color{hotpink}{r}\cos{\theta}\) ですから、
\(\displaystyle\tan{\theta}=\frac{\color{lime}{y}}{\color{deepskyblue}{x}}=\frac{\color{hotpink}{r}\sin{\theta}}{\color{hotpink}{r}\cos{\theta}}=\frac{\sin{\theta}}{\cos{\theta}}\)
よって、\(\displaystyle\tan{\theta}=\frac{\sin{\theta}}{\cos{\theta}}\) となります。

tan は傾きだから \(\frac{x}{y}\) で、\(y\) は sin、\(x\) は cos って覚えても良さそうだね!
sinとcosの関係

次は、sinとcosの関係についてやっていくよ!
sinとcosの間には、次のような関係が成り立ちます。
\(\sin{^2}\theta+\cos{^2}\theta=1\)
※ 「\(\sin{^2}\theta\)」は、「\(\sin\theta\) の2乗」のことです(\({\sin\theta}{^2}\)だと「角度θの2乗」という意味になっちゃいます!)。
なぜ成り立つのか、理由を分かりやすく解説

この直角三角形に、三平方の定理を使うと、\(\color{deepskyblue}{x^2}+\color{lime}{y^2}=\color{hotpink}{r^2}\)
そして、\(\color{deepskyblue}{x}=\color{hotpink}{r}\cos{\theta}\)、\(\color{lime}{y}=\color{hotpink}{r}\sin{\theta}\) ですから、代入して
\(\color{hotpink}{r^2}\cos{^2}\theta+\color{hotpink}{r^2}\sin{^2}\theta=\color{hotpink}{r^2}\)
よって、\(\sin{^2}\theta+\cos{^2}\theta=1\) となります。

元々は三平方の定理って考えれば覚えやすそう!
cosとtanの関係

次は、cosとtanの関係についてやっていくよ!
cosとtanの間には、次のような関係が成り立ちます。
\(\displaystyle 1+\tan{^2}\theta=\frac{1}{\cos{^2}\theta}\)
なぜ成り立つのか、理由を分かりやすく解説
sinとcosの関係式 \(\sin{^2}\theta+\cos{^2}\theta=1\) の両辺を \(\cos{^2}\theta\) で割ると
\(\displaystyle\frac{\sin{^2}\theta}{\cos{^2}\theta}\) \(\displaystyle+\frac{\cos{^2}\theta}{\cos{^2}\theta}=\frac{1}{\cos{^2}\theta}\)
ここで、\(\displaystyle\tan{\theta}=\frac{\sin{\theta}}{\cos{\theta}}\) より、\(\displaystyle\tan{^2}{\theta}=\frac{\sin{^2}{\theta}}{\cos{^2}{\theta}}\) ですから、
\(\displaystyle 1+\tan{^2}\theta=\frac{1}{\cos{^2}\theta}\) となります。

sinとcosの関係式からcosを消してあげるってことだね!
一応、sinとtanの関係式も

あれ、板書にはsinとtanの関係式はなかったよ?

そうなんだ。教科書にも載ってないし、今までの関係式があれば必要ないんだけど、一応やっておこうか。
sinとtanの間には、次のような関係が成り立ちます。
\(\displaystyle 1+\frac{1}{\tan{^2}\theta}=\frac{1}{\sin{^2}\theta}\)
なぜ成り立つのか理由を分かりやすく解説!
sinとcosの関係式 \(\sin{^2}\theta+\cos{^2}\theta=1\) の両辺を \(\sin{^2}\theta\) で割ると
\(\displaystyle\frac{\sin{^2}\theta}{\sin{^2}\theta}+\)\(\displaystyle\frac{\sin{^2}\theta}{\cos{^2}\theta}\) \(\displaystyle=\frac{1}{\sin{^2}\theta}\)
ここで、\(\displaystyle\tan{\theta}=\frac{\sin{\theta}}{\cos{\theta}}\) の逆数 \(\displaystyle \frac{1}{\tan{\theta}}=\frac{\cos{\theta}}{\sin{\theta}}\) より、\(\displaystyle\frac{1}{\tan{^2}{\theta}}=\frac{\cos{^2}{\theta}}{\sin{^2}{\theta}}\) ですから、
\(\displaystyle 1+\tan{^2}\theta=\frac{1}{\sin{^2}\theta}\) となります。

今度は、sinとcosの関係式からsinを消してあげるんだね。
三角比の相互関係を使った例題

三角比の相互関係を使って、次の例題を解いてみよう!

よろしくお願いします!
\(\theta\) は鋭角とする。\(\sin\theta=\frac{2}{3}\) のとき、\(\cos\theta\) と \(\tan\theta\) の値を求めよ。
sinの値から、cosとtanの値を求めます。
sinからcosを求める
まずは、sinとcosの関係式 \(\sin{^2}\theta+\cos{^2}\theta=1\) を使って、cosの値を求めていきます。
基本的な解き方
sinの値を \(\sin{^2}\theta+\cos{^2}\theta=1\) にそのまま代入していきます。
\(\sin\theta=\frac{2}{3}\) ですので、
\(\left(\frac{2}{3}\right)\)\({^2}+\cos{^2}\theta=1\)
これを計算すると
\(\cos{^2}\theta=\frac{5}{9}\)
あとは、2乗をはずして、\(\cos\theta=±\sqrt{\frac{5}{9}}=±\frac{\sqrt{5}}{3}\)
••• とやってしまいがちですが、これは間違いです。
問題文を確認すると、「\(\theta\) は鋭角とする」と書いてありましたね。
「cosはx座標」でしたので、単位円で符号を確認すると、
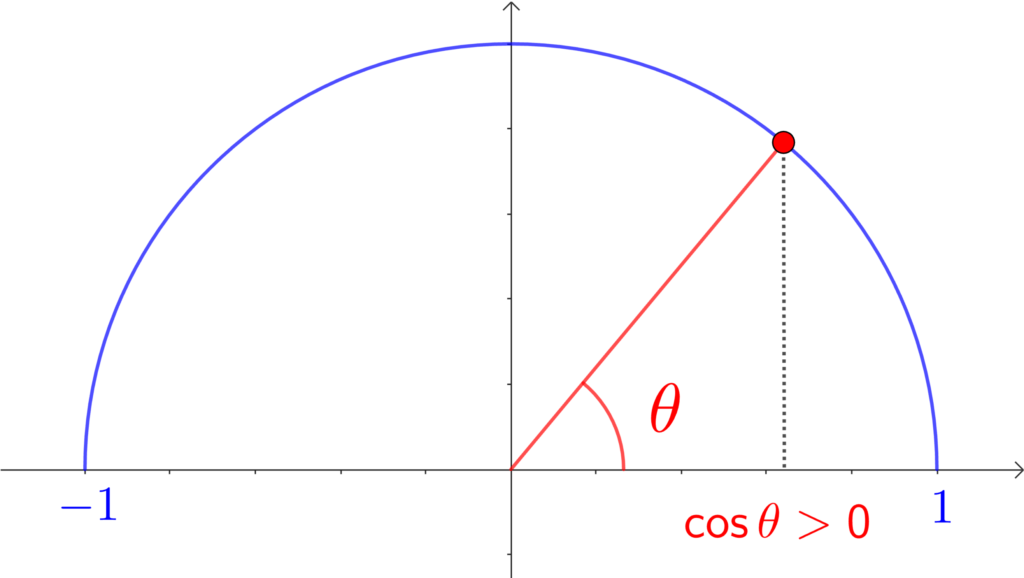
\(\theta\) が鋭角のとき、\(\cos\theta\) は + ですから、
\(\cos\theta=\sqrt{\frac{5}{9}}=\frac{\sqrt{5}}{3}\)
が正解ですね。

θの範囲をちゃんと確認する癖をつけておかないと間違えそう!
慣れてきた人の解き方
この解き方に慣れてきた人は、もう少しスマートな解き方に挑戦してみましょう。
それは、「\(\sin{^2}\theta+\cos{^2}\theta=1\) をあらかじめ \(\cos=\) の式に変形しておき、\(\sin\) の値を代入する」という方法です。
\(\sin{^2}\theta+\cos{^2}\theta=1\) を、\(\cos{^2}\theta=1-\sin{^2}\theta\) と変形し、
\(\cos{^2}\theta=1-\sin{^2}\theta\)
θの範囲を考慮しながら、2乗をとってあげると
\(\cos\theta=\sqrt{1-\sin{^2}\theta}\)
ここに、\(\sin\theta=\frac{2}{3}\) を代入していきます。
スマートな解答はこちら↓
\(\cos\theta>0\) より
sinとcosからtanを求める
sinとcosの値が分かったら、\(\displaystyle\tan{\theta}=\frac{\sin{\theta}}{\cos{\theta}}\) を使ってtanを求めていきましょう。
\(\sin\theta=\frac{2}{3}\) 、\(\cos\theta=\frac{\sqrt{5}}{3}\) ですから、
\(\displaystyle\tan{\theta}=\frac{\color{deepskyblue}{\frac{2}{3}}}{
\color{lime}{\frac{\sqrt{5}}{3}}}=\frac{2}{\sqrt{5}} \)
これでおしまいです!
※ 三角比の単元は基本的に「有理化」せずに答えるのが一般的です。
※ sinとtanの関係式:\(1+\frac{1}{\tan{^2}\theta}=\frac{1}{\sin{^2}\theta}\) からtanを求めることもできますが、計算がめんどくさいので、基本は使いません。
まとめ:三角比の相互関係

さて、今回のまとめだよ!
三角比の相互関係について勉強しました。
① sin と cos と tan の関係式:\(\displaystyle\tan{\theta}=\frac{\sin{\theta}}{\cos{\theta}}\)
② sin と cos の関係式:\(\sin{^2}\theta+\cos{^2}\theta=1\)
③ cos と tan の関係性:\(\displaystyle 1+\tan{^2}\theta=\frac{1}{\cos{^2}\theta}\)
\(\theta\) は鋭角とする。\(\color{deepskyblue}{\sin\theta=\frac{2}{3}}\) のとき、\(\color{lime}{\cos\theta}\) と \(\color{hotpink}{\tan\theta}\) の値を求めよ。
\(\cos\theta>0\) より

また一つ賢くなった!






コメント