【数学Ⅰ】三角比08：90°-θと180°-θの公式

---

---

「人より勉強に時間がかかる」と感じていませんか？

私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。

教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。

でも大丈夫！

このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。

「噛み砕き方」がわかれば、文章はぐっと読みやすくなります！

90°-θと180°-θの三角比

教科書には「90°-θの三角比」や「180°-θの三角比」の公式が載っています。

ですが、この公式をそのまま覚えてもあまり意味がありません。

なぜなら、「90°+θ」、「θ-90°」、「180°+θ」など他にもたくさんの種類があるからです。

そこで、「これだけ暗記して、あとはその場で考えればOK」というものを紹介します。

それがこちら。

これだけでは、まだわからないと思いますので、例題をつかって具体的に考えていきましょう。

例題で具体的に考える

① 関数の変化を考える

まずは「① 関数の変化を考える」です。

最初に、90°なのか、それとも180°なのかを確認します。

(1) \(\displaystyle\tan(90°-\theta)\) は 90° 、(2) \(\cos(180°+\theta)\) は 180° です。

そして、90°であれば、関数を変化させましょう。

「 \(\sin\) は \(\cos\) 」に、「 \(\cos\) は \(\sin\) 」に、「 \(\tan\) は \(\frac{1}{\tan\theta}\) 」に変化させます。

180°のときは関数を変化させる必要はありません。

ですので、

となります。

符号は次で考えるので、とりあえずは◻︎にしておきますね。

② ± を考える

次に「② ± を考える」です。

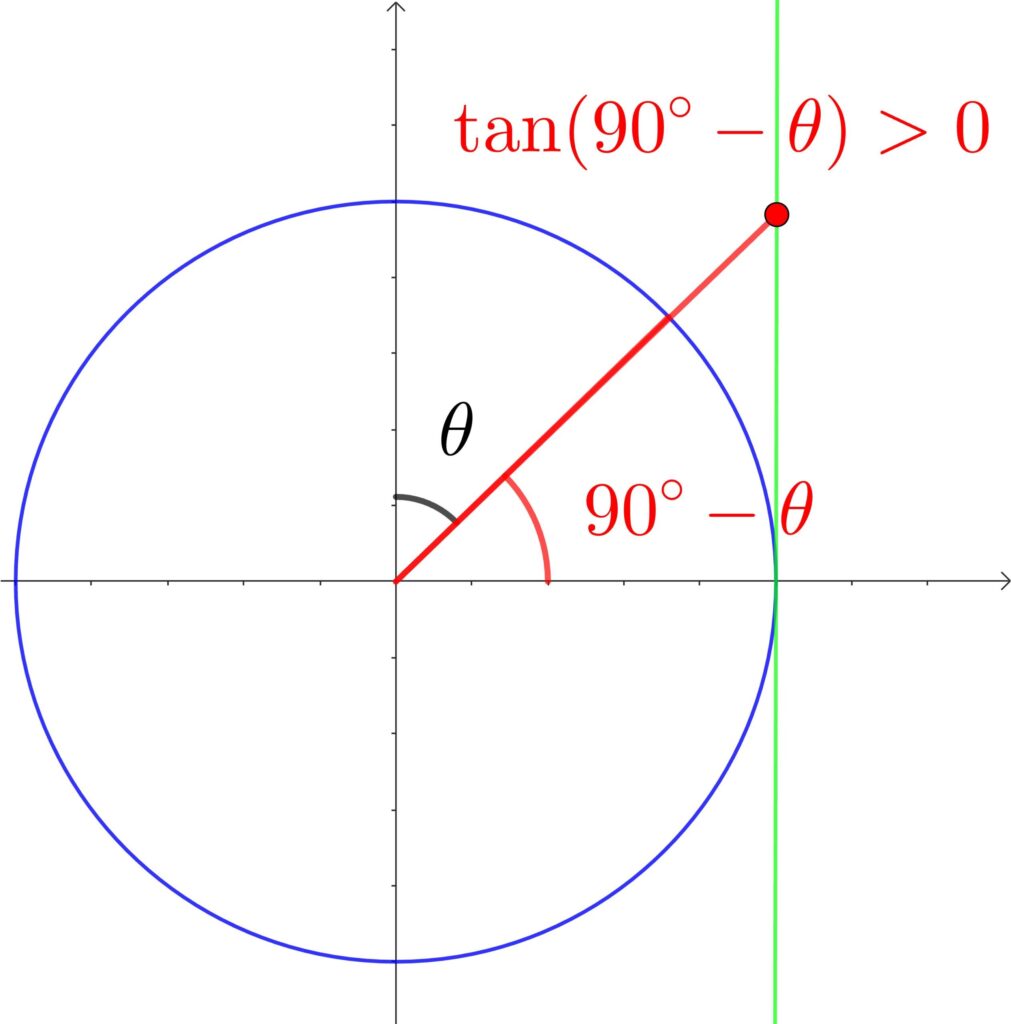
(1) \(\tan(90°-\theta)\) の ± を単位円を使って考えていきましょう。

まずは単位円を描きます。

そして、鋭角のθを使って、90°-θを描きます。

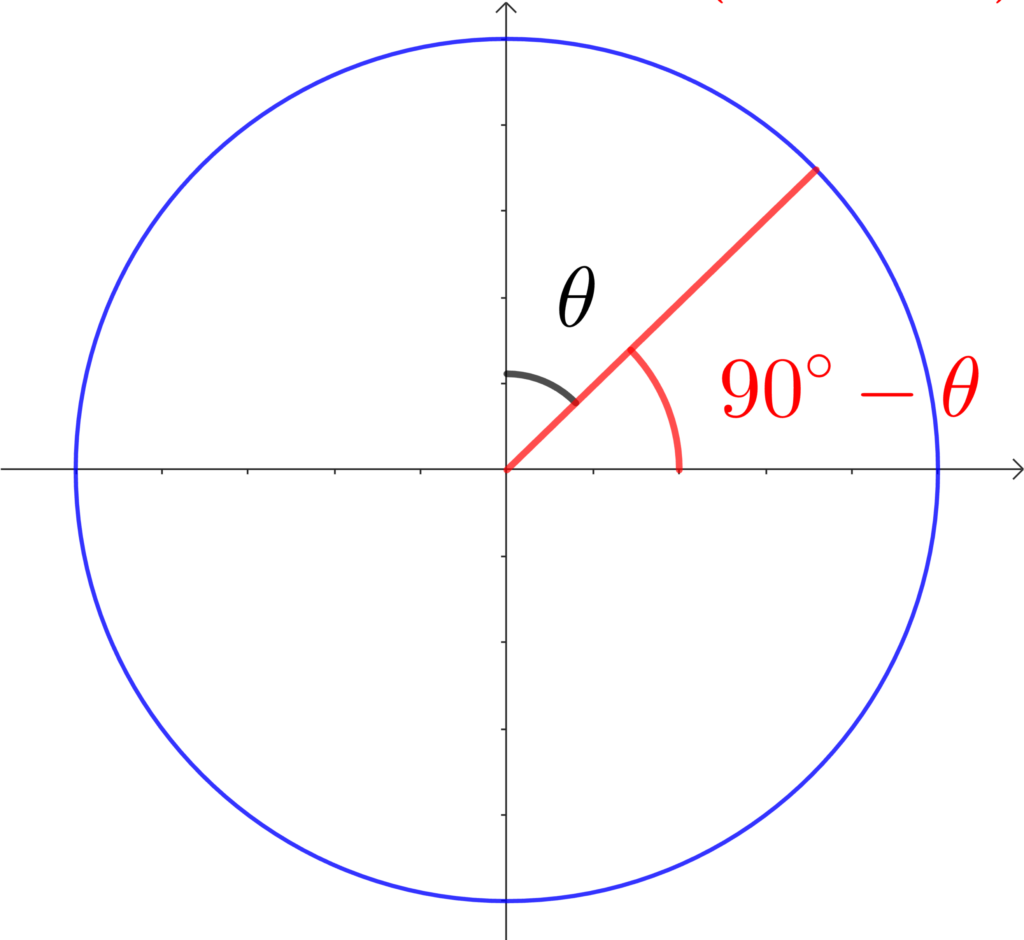
あとは、この角の \(\tan\) の ± を判断します。

「\(\tan\) は \(x=1\) の\(y\) 座標」ですから、\(\tan(90°-\theta)\) の符号は + ですね。

よって、

と導けるわけです。

---

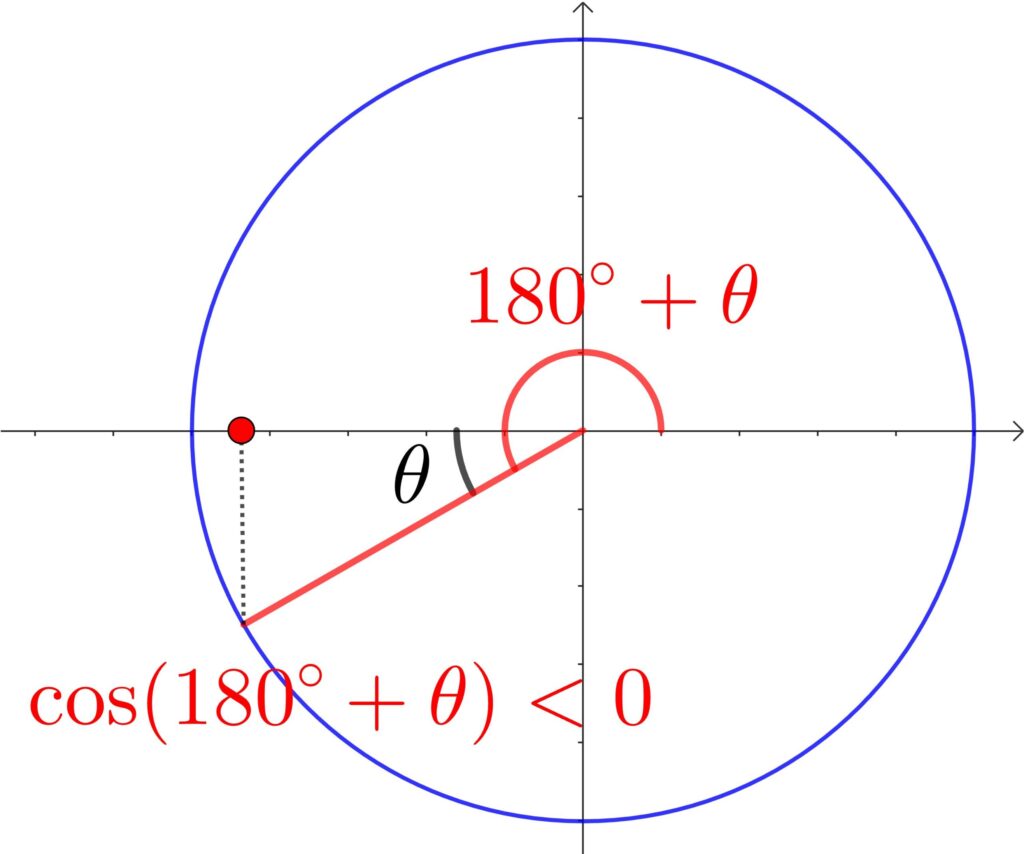
(2) \(\cos(180°+\theta)\) の ± も単位円を使って考えていきましょう。

まずは単位円を描きます。

そして、鋭角のθを使って、180°+θを描きます。

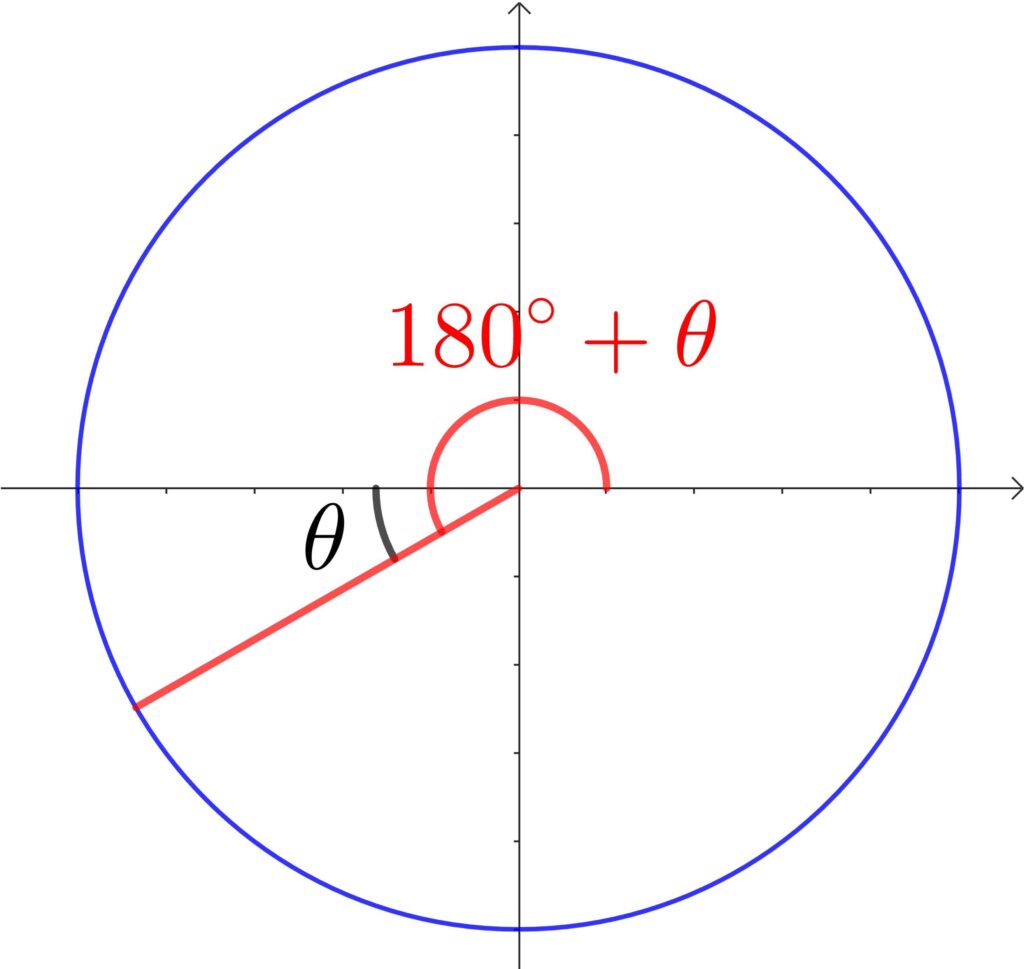
あとは、この角の \(\cos\) の ± を判断します。

「\(\cos\) は \(x\) 座標」ですから、\(\cos(180°-\theta)\) の符号は – ですね。

よって、

と導けるわけです。

90°-θと180°-θの公式が成り立つ理由

90°-θの公式が成り立つ理由

次の直角三角形を使って考えていきます。

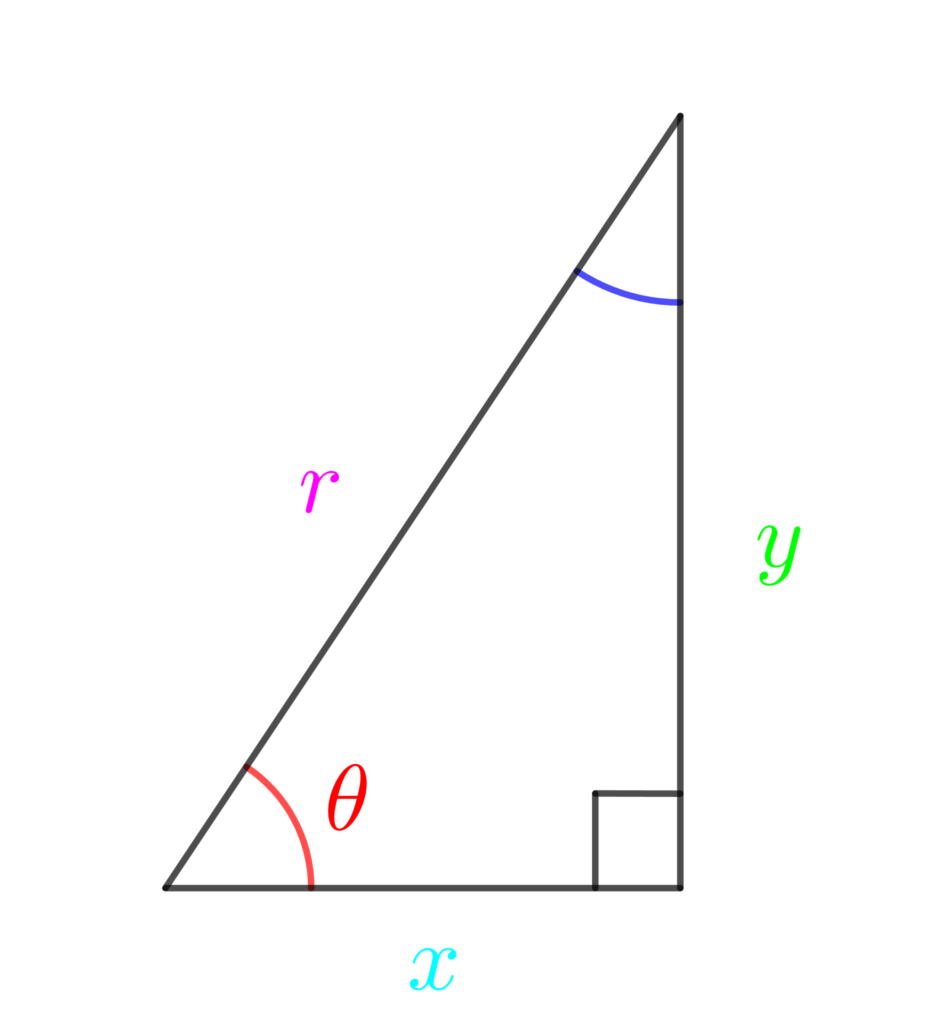
青の角度はいくつでしょうか？

三角形の内角の和は180°ですので、180° – θ – 90° = 90° – θ ですね。

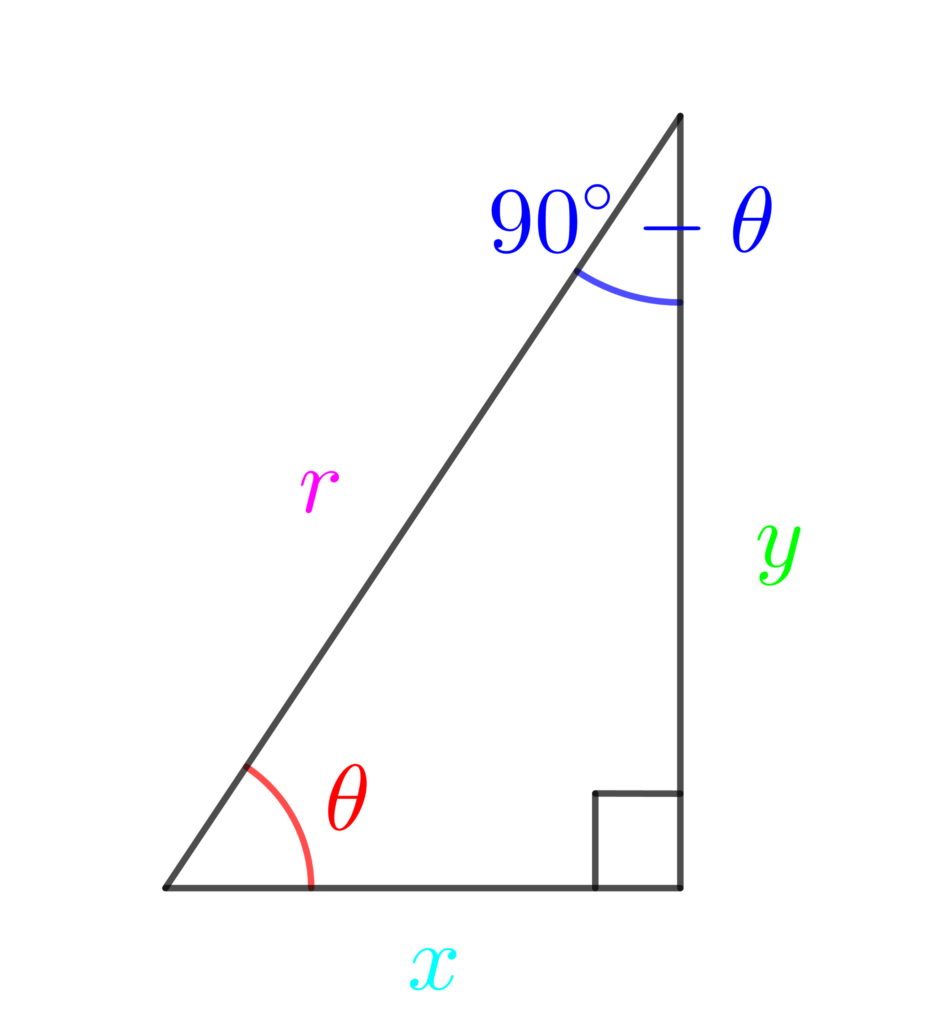
この直角三角形の向きを変えてみます。

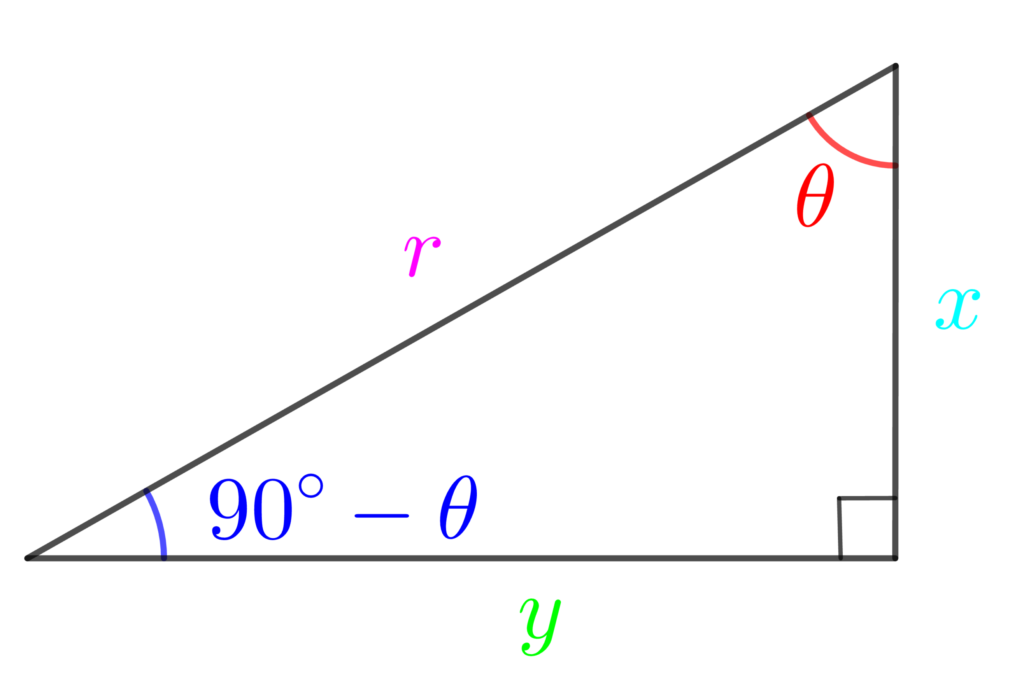
では、「90°の三角比」と「90° – θの三角比」を比べてみましょう。

「90°の三角比」と「90° – θの三角比」を比べてみると、関数が変化することがわかりますね。

180°-θの公式が成り立つ理由

角度θを単位円で表し、点Pの座標を \((x, y)\) とします。

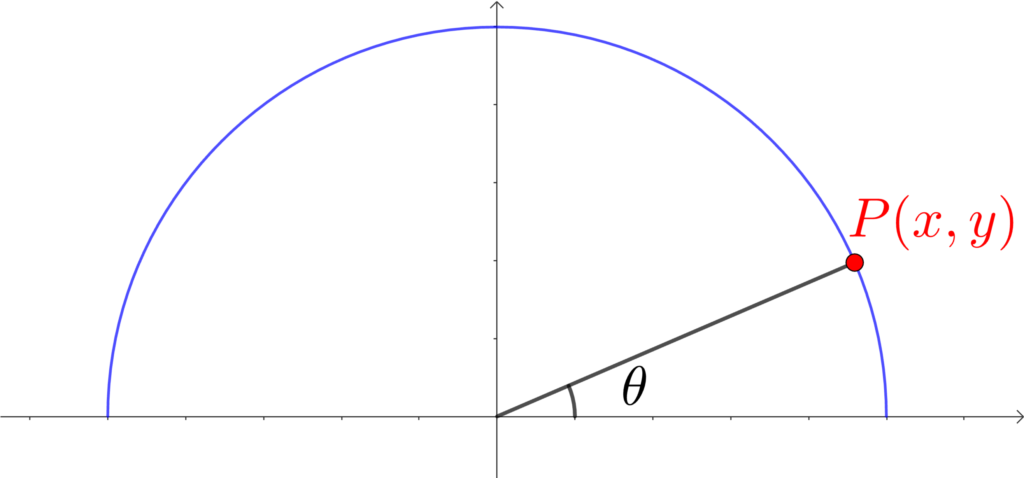
そして180°-θの角度を表すと

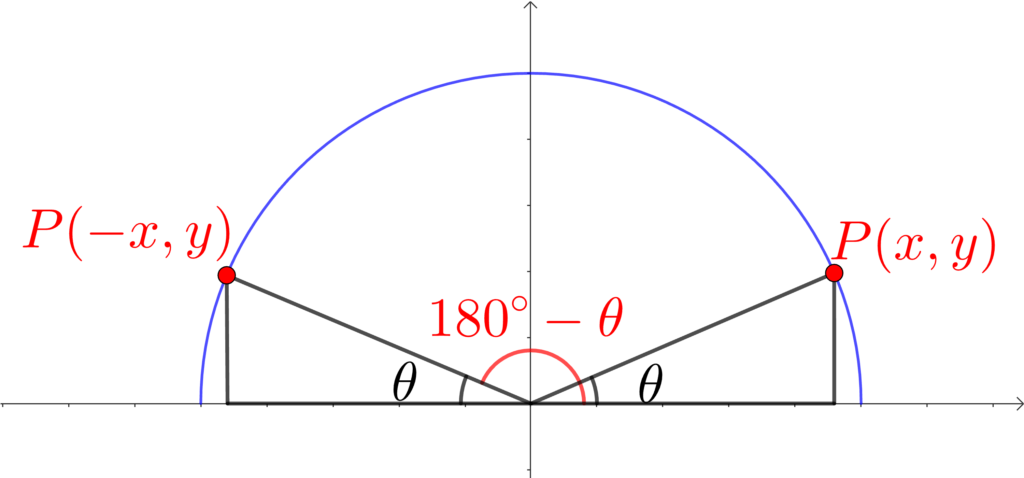
ここで、点Pの \(x\) 座標 が \(\cos\)、\(y\) 座標が\(\sin\) でした。

\(y\) 座標を比較すると、

\(\sin{\theta}=\sin{(180°-\theta)}\) より \(\sin{(180°-\theta)}=\sin{\theta}\)

\(x\) 座標を比較すると 、

\(\cos{\theta}=-\cos{(180°-\theta)}\) より \(\cos{(180°-\theta)}=-\cos{\theta}\)

そして、sin と cos と tan の関係式を使うと、

まとめ：三角比の相互関係

三角比の相互関係について勉強しました。

---

---