【数学A】場合の数01：集合の要素の個数

さん

今日の板書はこれ！

2つの集合の和集合の要素の個数

\(n(A \cup B)=n(A)+n(B)-n(A\cap B)\)

（\(n(A\cap B)=\phi\)のときは \(n(A \cup B)=n(A)+n(B)\)）

補集合の要素の個数

\(n(\overline{A})=n(U)-n(A)\)

3つの集合の和集合の要素の個数

↓横にスライドしてね↓

\( \begin{aligned} \displaystyle \color{red}{n(A \cup B \cup C)=n(A)+n(B)+n(C)-n(A\cap B)-n(B\cap C)-n(C\cap A)+n(A\cap B\cap C)} \\ \\ \end{aligned} \)

生徒

もっと詳しく願いします！！

現役教員として数学を教えている「さん」と申します。

「人より勉強に時間がかかる」と感じていませんか？

私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。

• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」

• 「解答の意味が理解できず、勉強が進まない」

教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。

でも大丈夫！

このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。

意味から理解し、噛み砕き方をマスターしましょう！！

勉強しても成績が上がらない3つの理由と現役教師が教えるたった1つの解決策

一生懸命やってるのに結果が出ない…そんな中高生の悩みを、現役教師が本気で解決！信頼できる家庭教師が導く正しい学び方とは？

集合の要素の個数
まとめ：三角比による三角形の面積

集合の要素の個数

さん

集合の中に要素が何個あるのかを数えていこう！

集合の要素の個数を \(n(A)\) で表すことができます。

例えば、集合\(A=\{1, 2, 3, 4\}\) とすると、要素は４つあるので \(n(A)=4\) となります。

同様に、集合\(B=\{2, 4, 6\}\) なら \(n(B)=3\) です。

2つの集合の和集合の要素の個数

\(n(A \cup B)=n(A)+n(B)-n(A\cap B)\)

（\(n(A\cap B)=\phi\)のときは \(n(A \cup B)=n(A)+n(B)\)）

さん

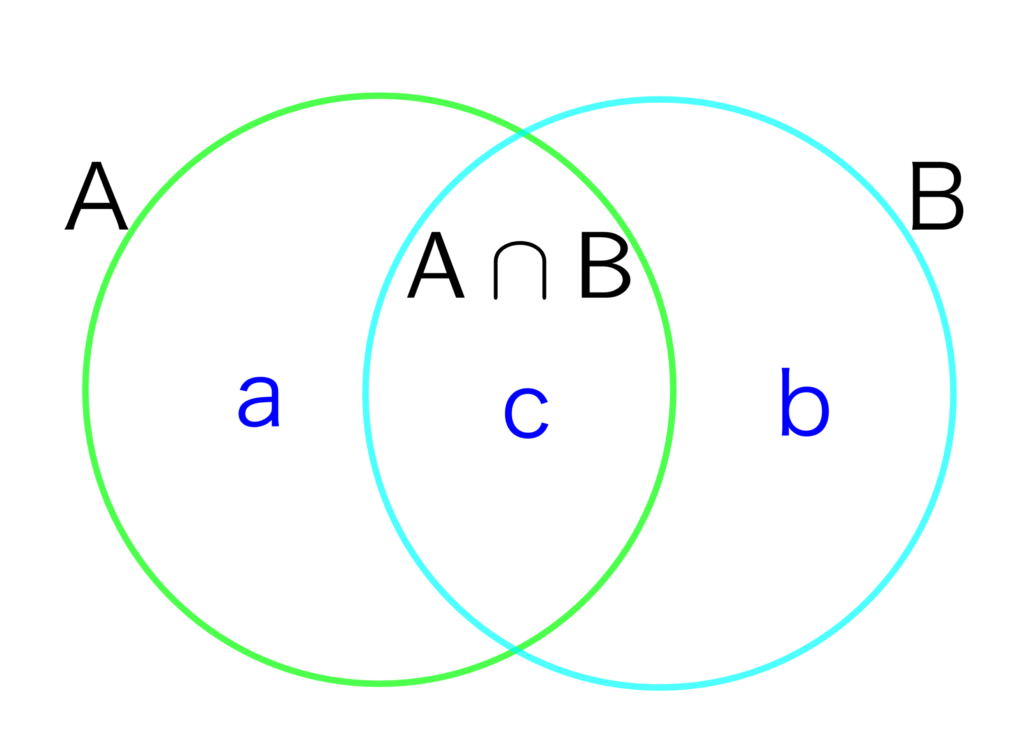
次の例題を使って勉強していこう！

例題１

全体集合\(U\) の部分集合\(A, B\) について \(n(A)=40\), \(n(A)=18\), \(n(B)=25\), \(n(A\cap B)=6\) であるとする。\(n(A\cup B)\) を求めよ。

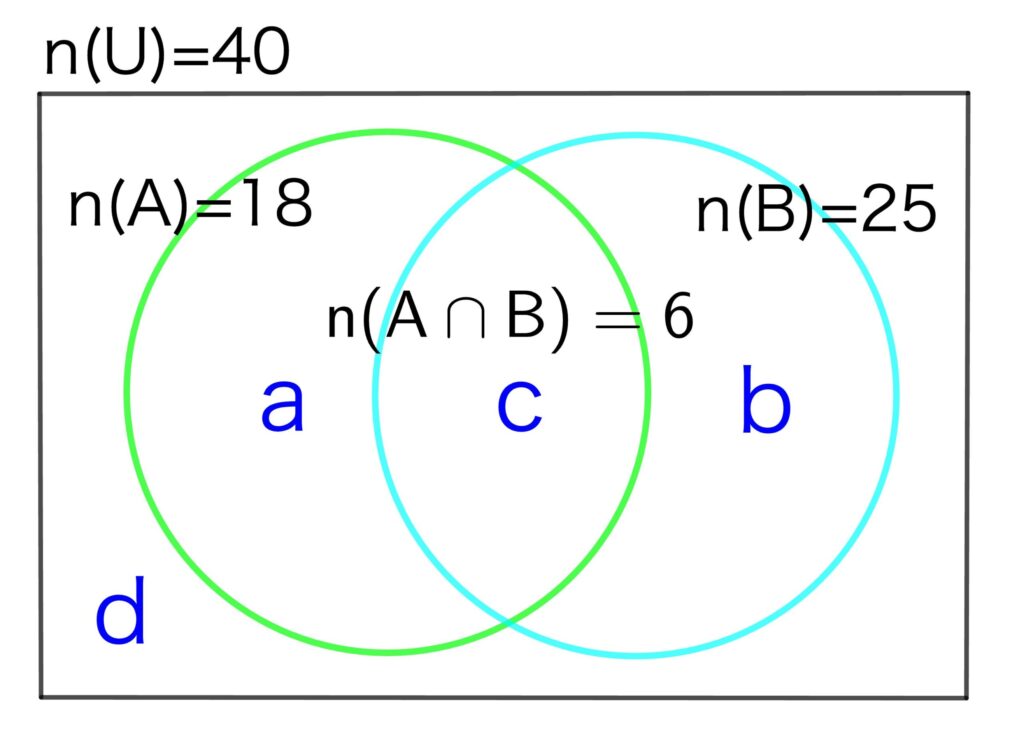
上のベン図では、領域が \(a\)〜\(d\) に分かれています。

\(n(U)=\color{blue}{a+b+c+d}=40\)

\(n(A)=\color{blue}{a+c}=18\)

\(n(B)=\color{blue}{b+c}=25\)

\(n(A\cap B)=\color{blue}{c}=6\) であり、

求めたいのは \(n(A\cup B)=\color{blue}{a+b+c}\) の個数です。

生徒

\(n(A\cup B)\) はAとBの和集合だから\(n(A)+n(B)\) を計算すればいいのかな？

さん

１度やってみようか！

\( \begin{aligned} \displaystyle n(A)+n(B)&=\color{blue}{(a+c)+(b+c)} \\ \\ &=\color{blue}{a+b+2c} \\ \end{aligned} \)

これでは、\(\color{blue}{c}\) が１個分余分に計算されてしまいます。

そこで、\(n(A\cap B)=\color{blue}{c}\) を１回引いてあげることで、辻褄を合わせましょう。

\( \begin{aligned} \displaystyle \color{red}{n(A\cup B)}&=\color{red}{n(A)+n(B)-n(A\cap B)} \\ \\ &=\color{blue}{(a+c)+(b+c)-c} \\ \\ &=\color{blue}{a+b+c} \\ \end{aligned} \)

\( \begin{aligned} \displaystyle \color{red}{n(A\cup B)}&=\color{red}{n(A)+n(B)-n(A\cap B)} \\ \\ &=18+25-6 \\ \\ &=37 \\ \end{aligned} \)

補集合の要素の個数

さん

次は、補集合の要素の個数について例題を使って考えていこう！

補集合の要素の個数

\(n(\bar{A})=n(U)-n(A)\)

例題２

全体集合\(U\) の部分集合\(A, B\) について \(n(A)=40\), \(n(A)=18\), \(n(B)=25\), \(n(A\cap B)=6\) であるとする。\(n(\bar{A})\) を求めよ。

\(n(U)=\color{blue}{a+b+c+d}=40\)

\(n(A)=\color{blue}{a+c}=18\)

\(n(B)=\color{blue}{b+c}=25\)

\(n(A\cap B)=\color{blue}{c}=6\)

\(n(A\cup B)=\color{blue}{a+b+c}=6\)

今回求めたいのは \(n(\bar{A})=\color{blue}{b+d}\) の個数です。

「補集合\(\bar{A}\)の要素の個数」は、「全体集合の要素の個数」から「集合Aの要素の個数」を引けば求めることができます。

\( \begin{aligned} \displaystyle \color{red}{n(\bar{A})}&=\color{red}{n(U)-n(A)} \\ \\ &=\color{blue}{(a+b+c+d)-(a+c)} \\ \\ &=\color{blue}{b+d} \\ \end{aligned} \)

\( \begin{aligned} \displaystyle \color{red}{n(\bar{A})}&=\color{red}{n(U)-n(A)} \\ \\ &=40 – 18 \\ \\ &=22 \\ \end{aligned} \)

3つの集合の和集合の要素の個数

さん

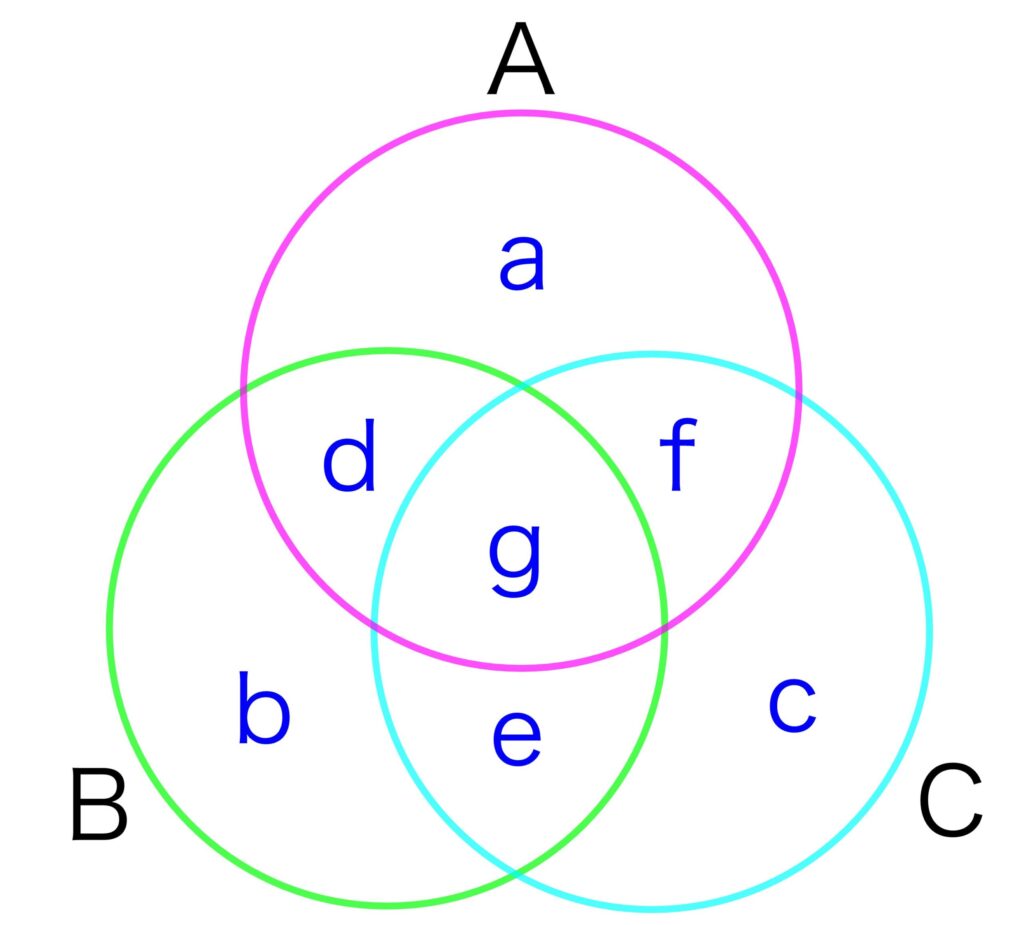
AとBとCの和集合の個数を求めていこう！

今回考える集合は次の集合です。

\( \begin{aligned} \displaystyle n(A\cup B \cup C)=\color{blue}{a+b+c+d+e+f+g} \end{aligned} \)

「2つの集合の和集合の要素の個数」と同じように「足しすぎた分を後から引く」という考え方で求めていきましょう。

\( \begin{aligned} \displaystyle n(A)+n(B)+n(c)&=\color{blue}{(a+d+f+g)+(b+d+e+g)+(c+e+f+g)} \\ \\ &=\color{blue}{a+d+c+2d+2e+2f+3g} \end{aligned} \)

このままでは \(\color{blue}{d, e, f, g}\) が余分に足されてるので、次の３つを引いてあげます。

\(n(A\cap B)=\color{blue}{d+g}\)

\(n(B\cap C)=\color{blue}{e+g}\)

\(n(C\cap A)=\color{blue}{f+g}\)

\( \begin{aligned} \displaystyle n(A)+n(B)+n(c)-n(A\cap B)-n(B\cap C)-n(C\cap A)&=\color{blue}{(a+d+f+g)+(b+d+e+g)+(c+e+f+g)-(d+g)-(e+g)-(f+g)} \\ \\ &=\color{blue}{a+d+c+d+e+f} \end{aligned} \)

生徒

あれ、\(\color{blue}{g}\) を引き過ぎちゃった•••

\(\color{blue}{g}\) がなくなってしまったので、\(n(A\cap B\cap C)=\color{blue}{g}\) を足して調節してあげます。

\( \begin{aligned} \displaystyle n(A)+n(B)+n(c)-n(A\cap B)-n(B\cap C)-n(C\cap A)+n(A\cap B\cap C)&=\color{blue}{(a+d+f+g)+(b+d+e+g)+(c+e+f+g)-(d+g)-(e+g)-(f+g)+g} \\ \\ &=\color{blue}{a+d+c+d+e+f+g} \end{aligned} \)

これで、3つの集合の和集合の要素の個数の完成です。

3つの集合の和集合の要素の個数

\( \begin{aligned} \displaystyle \color{red}{n(A \cup B \cup C)=n(A)+n(B)+n(C)-n(A\cap B)-n(B\cap C)-n(C\cap A)+n(A\cap B\cap C)} \\ \\ \end{aligned} \)

まとめ：三角比による三角形の面積

さん

さて、今回のまとめだよ！

2つの集合の和集合の要素の個数

\(n(A \cup B)=n(A)+n(B)-n(A\cap B)\)

（\(n(A\cap B)=\phi\)のときは \(n(A \cup B)=n(A)+n(B)\)）

補集合の要素の個数

\(n(\overline{A})=n(U)-n(A)\)

3つの集合の和集合の要素の個数

↓横にスライドしてね↓

\( \begin{aligned} \displaystyle \color{red}{n(A \cup B \cup C)=n(A)+n(B)+n(C)-n(A\cap B)-n(B\cap C)-n(C\cap A)+n(A\cap B\cap C)} \\ \\ \end{aligned} \)