
今日の板書はこれ!
異なる\(n\)個のものの円順列の総数は \((n-1)!\)
円順列は次の2つの考え方で、普通の順列と考えることだできる。
1.「1人を固定する」
2.「1人の目線になって考える」

もっと詳しく願いします!!
現役教員として数学を教えている「さん」と申します。
「人より勉強に時間がかかる」と感じていませんか?
私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。
• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」
• 「解答の意味が理解できず、勉強が進まない」
教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。
でも大丈夫!
このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。
意味から理解し、噛み砕き方をマスターしましょう!!
円順列
円順列の公式

次の例題で考えてみよう!
(1) \(5\)人を1列に並べるときの並べ方の総数を求めよ。
(2) \(5\)人を円に並べるときの並べ方の総数を求めよ。
5人(A, B, C, D, E) を(1)では1列にならべ、(2)では円形に並べます。

(1) は \(5!=120\) 通りだね!
(1)と(2)の違いを考えるために、具体的に考えていきましょう。
1列に並べたとき、次の並び方はすべて異なる並び方だと考えます。
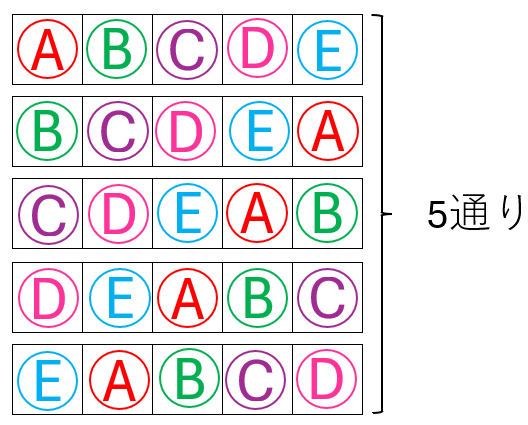
では、この5通りを円形に並べ直してみましょう。
一番左の人が上にくるように、反時計回りで並べます。
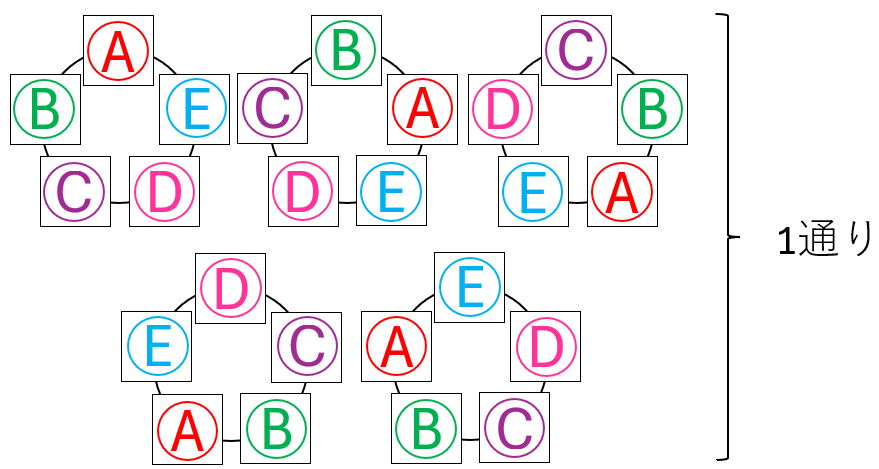
円に並べたとき、これら並び方は、すべて同じ並び方だと考えます。
円順列では、回転して一致するものはすべて同じものとみなすのです。
5通りの順列から、1通りの円順列が作れるので、(2)円順列の総数は、(1)順列の総数\(5!\)を\(5\)で割った、\(\displaystyle\frac{5!}{5}=4!\) と計算することができます。

グルグル回転させて同じになるやつは、全部一緒の並べ方なんだね!

円順列の総数は、順列の総数を、並べる人数で割ってあげれば求めれるってことだね!
「異なる\(n\)個のものの円順列の総数」を考えて、公式にしてみましょう。
「異なる\(n\)個のものの順列の総数」は \(n!\)通りであり、そのうち、\(n\)通りの順列から、\(1\)通りの円順列が作れるので、次のように計算することができます。
\(\displaystyle\frac{n!}{n}=\frac{n(n-1)!}{n}=(n-1)!\)
この公式は、原理を理解したうえで暗記しておきましょう。
例題
大人3人と子ども3人が輪の形に並ぶとき、次のような並べ方は何通りあるか。
(1) 子ども3人が続いて並ぶ。
(2) 大人と子どもが交互に並ぶ。
(1)は「隣接する順列」です。
隣接するものは、1組にまとめて全体を並べた後、組の中を並べる。
大人3人と子ども1組の並べ方は \((4-1)!=3!\)
子ども3人の並べ方は \(3!\)
よって、求める並べ方の総数は \(3!\cdot 3!=9\cdot 9=81\) 通り
(2)では、次のように並びます。
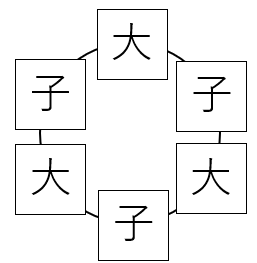
大人3人をA, B, C 子ども3人をa, b, c として考えていきます。
円順列の厄介なところは、「回転して一致するものはすべて同じものとみなす」ことです。

んー。回転しなければいいのに…。

実は回転しないように考える方法があるんだ!
それは「1人を固定する」という考え方です。
大人(A, B, C) 子ども(a, b, c)の中から、例えばAさんを先に並べて固定させます。
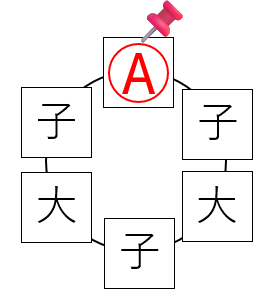
回転さえしなくなれば、後は普通の順列と同じです。
大人の並べ方が\(2!\)、子どもの並べ方が\(3!\)
よって、\(2!×3!=12\) 通り。

おーそんな方法があるのか!でもなんでそんなことができるの?

「Aさんを固定する」という考え方じゃなくて「Aさんの視点になる」という考え方なら納得できるかな?
「Aさんの視点」になって考えてみましょう。
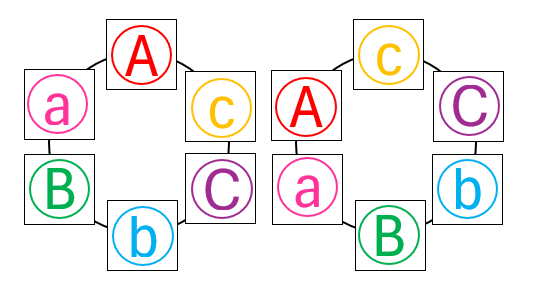
上の2つの並べ方で、Aさんの視点をイメージしてみてください。
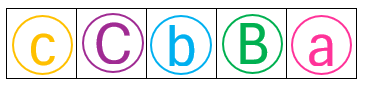
どちらも、同じ並び方に見えますね。
いくら回転しても「Aさんの視点」で考えると並び方は変わりません。
これが、「1人を固定する」の正体です。
Aさんの視点になることで、普通の順列の問題と捉えることがでるのです。
まとめ:円順列

さて、今回のまとめだよ!
異なる\(n\)個のものの円順列の総数は \((n-1)!\)
円順列は次の2つの考え方で、普通の順列と考えることだできる。
1.「1人を固定する」
2.「1人の目線になって考える」

ありがとうございました!!






コメント