【数学A】場合の数09：組合せ

---

---

現役教員として数学を教えている「さん」と申します。

「人より勉強に時間がかかる」と感じていませんか？

私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。

教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。

でも大丈夫！

このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。

意味から理解し、噛み砕き方をマスターしましょう！！

組合せ

組合せの考え方

組合せを考える前に、4個から3個選んで並べる順列を考えます。

これは \(_4P_3=4\cdot 3 \cdot 2=24\) 通りと計算することができました。

すべて書き出してみましょう。

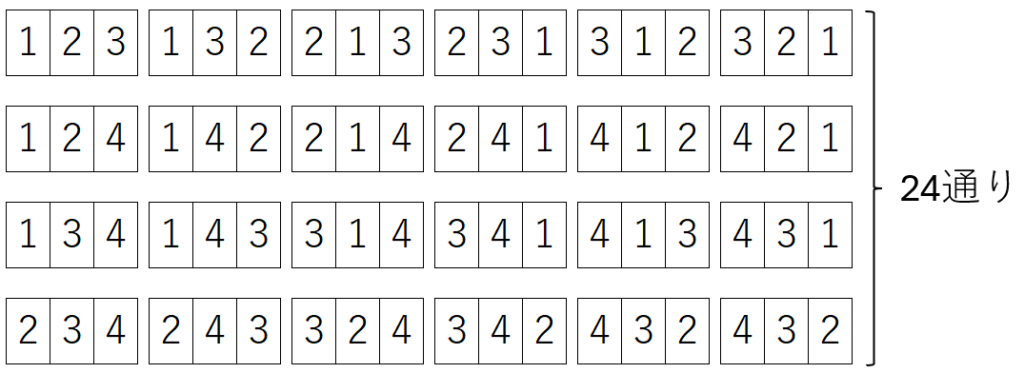
では、組合せを考えます。

「選んで並べる」のが順列でしたが、「選ぶ」までが組合せです。

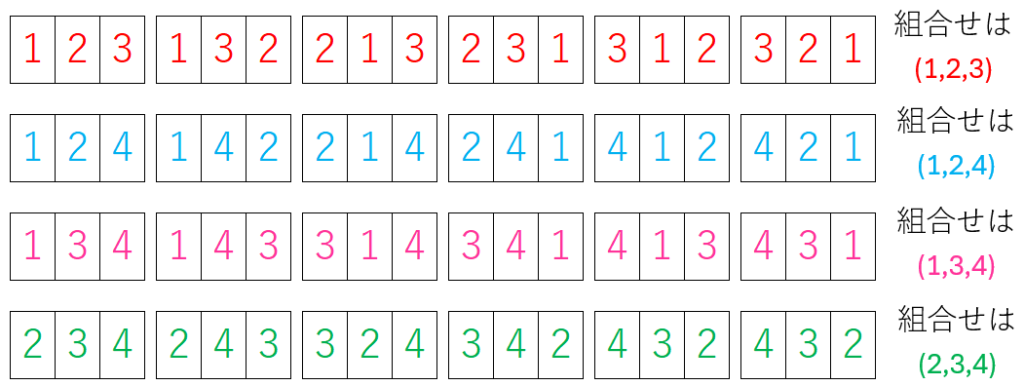
このように、順列は24通りありますが、組合せは4通りになります。

組合せは、順列を使用して求めます。

一旦選んで並べた後、その並び順を無視すると何通りになるかを考えます。

異なる3個のものを並べるときの順列の総数は\(3!\)通りですから、順列の総数\(_4P_3\)を\(3!\)で割って求めます。

\(\displaystyle\frac{_4P_3}{3!}=\frac{4\cdot 3\cdot 2}{3\cdot 2\cdot 1}=4\)

また、４人から３人選ぶ組合せの総数を「\(_4 C _3\) 」と表すことができ、「ヨン シー サン」と読みます。

これを一般化したのが次のものです。

順列と組合せの違い

順列と組合せの違い

(1)は「選んで並べる」ので順列、(2)は「選ぶだけ」なので組合せを考えます。

(1) \(_6P_4=6\cdot 5\cdot 4\cdot 3=360\)

(2) \(\displaystyle_6C_4=\frac{6\cdot 5\cdot 4\cdot 3}{4\cdot 3\cdot 2\cdot 1}=15\)

組合せの計算のポイント

ここで、計算のポイントがあります。

それは、「6人から4人を選ぶことは、６人から2人を選ぶことと等しい」ということです。

例えば6人「A, B, C, D, E, F」から、4人「A, B, C, D」を選ぶということは、2人「E, F」を選ぶとも言えるのです。

ですから、\(\displaystyle_6C_4=_6C_2=\frac{6\cdot 5}{2\cdot 1}=15\) と計算することができるのです。

「100人から98人を選ぶ組合せ」は次の計算をするより、

\(\displaystyle_{100}C_{98}=\frac{100\cdot 99\cdots 2\cdot 1}{98\cdot 97\cdots 2\cdot 1}\)

「100人から2人を選ぶ組合せ」を計算するほうが計算が楽になります。

\(\displaystyle_{100}C_{98}=_{100}C_{2}=\frac{100\cdot 99}{2\cdot 1}\)

組合せの階乗表現

また、\(\displaystyle_{6}P_{4}=\frac{6!}{2!}\) と表すことができました。

ですので、組合せも \(\displaystyle_{6}P_{4}=\frac{_{6}P_{4}}{2!}=\frac{6!}{4!2!}\) と階乗のみで表すことができます。

一般化すると \(\displaystyle_nC_r=\frac{n!}{r!(n-r)!}\) となります。

まとめ：組合せ

---

---