
今日の板書はこれ!
直線…異なる2点で1本定まる。
異なるn個の点のうち2点を結んでできる直線の本数は\(_nC_2\) 本
三角形…同じ直線上にない3点で1個定まる。
どの3点も同一直線上にないn個の点を結んでできる三角形の個数は\(_nC_3\) 個

もっと詳しく願いします!!
現役教員として数学を教えている「さん」と申します。
「人より勉強に時間がかかる」と感じていませんか?
私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。
• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」
• 「解答の意味が理解できず、勉強が進まない」
教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。
でも大丈夫!
このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。
意味から理解し、噛み砕き方をマスターしましょう!!
図形の個数

次の例題を考えよう!
正六角形ABCDEFについて、次の数を求めよ。
(1) 2点の頂点を結ぶ線分の本数
(2) 対角線の本数
(3) 3個の頂点を結んでできる三角形の個数
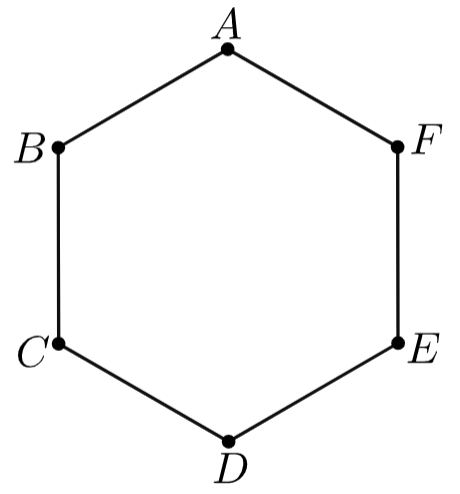
線分の本数
(1) では 線分の本数を数えます。
直線は、異なる2点で1本定まります。
例えば、6個の頂点からAとCを選ぶと次のような線分が1つ定まります。
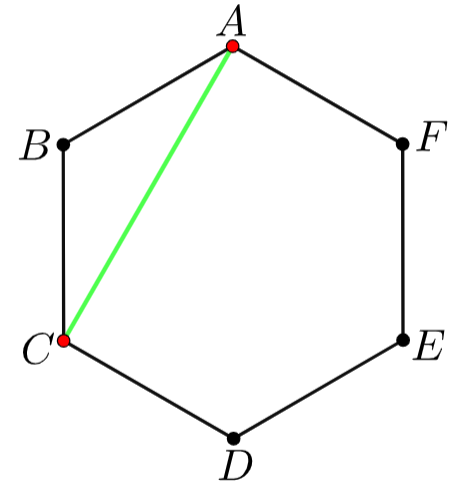
ですから、6個の頂点から2個の頂点を選ぶ組合せの総数を求めればよいわけです。
\(\displaystyle_6C_2=\frac{6\cdot 5}{2\cdot 1}=15\) 本

直線は2個の頂点を選べばいいんだね!
対角線の本数
(2)では対角線の本数を数えます。
そもそも「対角線」とは「隣り合っていない2つの頂点を結ぶ線分」のことです。

じゃあ隣り合っている2つの頂点を結ぶ線分は?

それは「辺」っていうんだ!
ですから、\((対角線)=(2点の頂点を結ぶ線分)-(辺)\) で求めることができます。
(1) より \(15-6=9\) 本
三角形の個数
最後に (3) で三角形の個数を数えます。
三角形は、同じ直線上にない3点で1個定まります。
例えば、6個の頂点からAとCとFを選ぶと次のような三角形が1つ定まります。
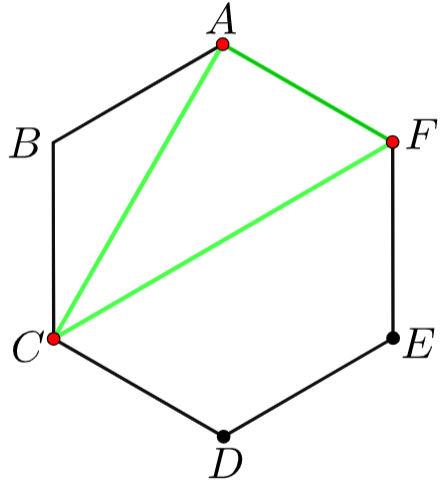
ですから、6個の頂点から3個の頂点を選ぶ組合せの総数を求めればよいわけです。
\(\displaystyle_6C_3=\frac{6\cdot 5\cdot 4}{3\cdot 2\cdot 1}=20\) 個

三角形は3個の頂点を選べばいいんだね!
まとめ:図形の個数

さて、今回のまとめだよ!
直線…異なる2点で1本定まる。
異なるn個の点のうち2点を結んでできる直線の本数は\(_nC_2\) 本
三角形…同じ直線上にない3点で1個定まる。
どの3点も同一直線上にないn個の点を結んでできる三角形の個数は\(_nC_3\) 個

ありがとうございました!!






コメント