【数学A】場合の数12：区別のない組合せ

---

---

現役教員として数学を教えている「さん」と申します。

「人より勉強に時間がかかる」と感じていませんか？

私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。

教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。

でも大丈夫！

このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。

意味から理解し、噛み砕き方をマスターしましょう！！

区別のある組合せと区別のない組合せ

区別のある組合せ

(1)は、「区別のある2つの部屋に4人（①～④）を分ける」組合せの問題です。

4人を部屋Aと部屋Bに2人ずつ分けます。

部屋Aに入る2人の選び方は、4人の中から2人を選ぶ組合せなので \(_4C_2=6\) 通りです。

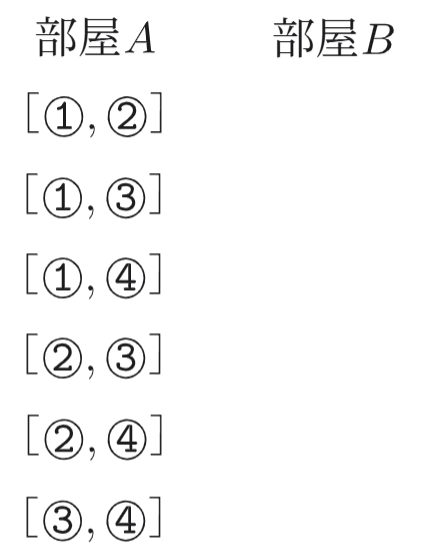
次に、部屋Bに入る2人は、残りの2人で決まるため、 \(_2C_2=1\) 通りとなります。

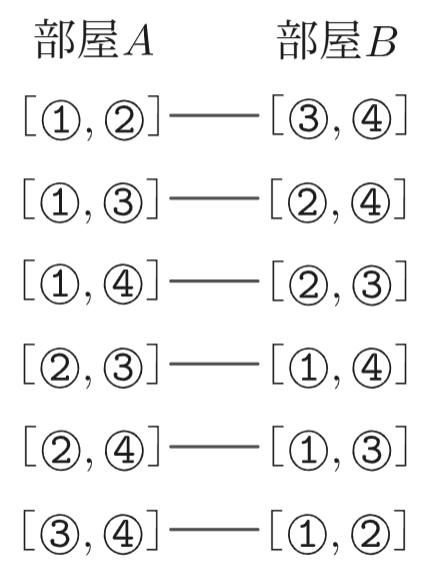
したがって、4人をA・Bの2つの部屋に2人ずつ分ける方法は \(_4C_2×_2C_2=6\) 通りです。

区別のない組合せ

(2)は、(1)とは違って、2つの部屋に区別がない場合の問題です。

(1)では、「部屋A」「部屋B」と区別して分けたため、次のような分け方は別のものとして数えました。

しかし今回は、ただ2人ずつに分けるだけ。

その場合、次のような分け方はどうでしょうか。

赤、青、緑の分け方は、それぞれ同じ分け方とみなされます。

したがって、重複している分だけ、 \(2!\) （＝部屋の入れ替え方の数）で割る必要があります。

よって、\(\displaystyle\frac{_4C_2×_2C_2}{2!}=3\) 通りとなります。

(1) は「2人組に分けたあと，区別のある部屋に並べる」。

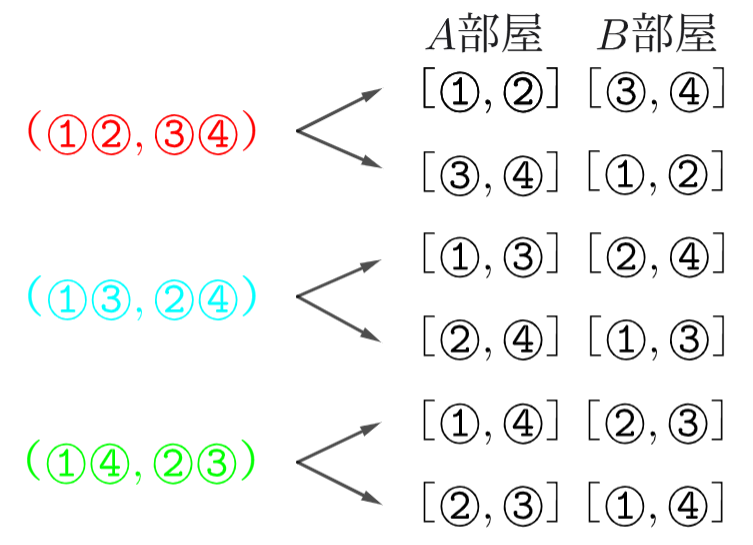
(2) は「2人組に分けるだけ」。

したがって、(1) の結果から「部屋の並べ方」による重複 \(2!\) を割れば、(2) の答えになります。

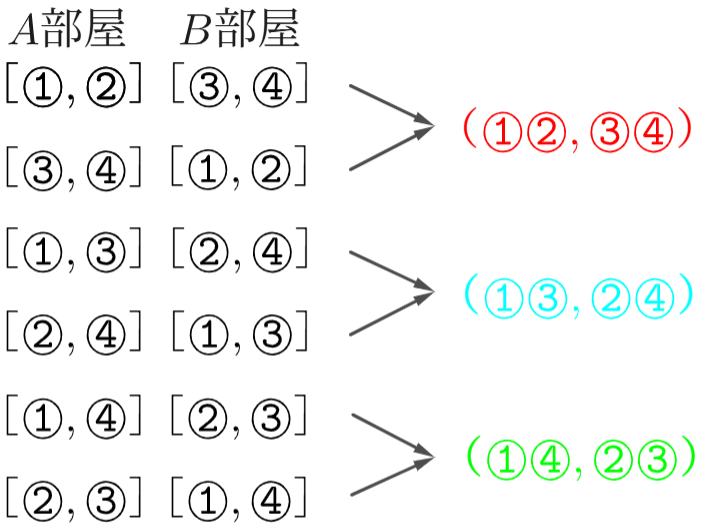
\(\displaystyle\frac{_4C_2×_2C_2}{2!}=3\) 通り

例題

---

(1) は、部屋に区別のある組合せです。

まず、部屋Aに入る2人の組合せは \(_8C_2\) 通りです。

次に、その組合せそれぞれに対して、部屋Bに入る2人の組合せは \(_6C_2\) 通り

同様に、部屋Cに入る組合せは \(_4C_2\) 通り

最後に部屋Dに入る組合せは \(_2C_2\) 通り

したがって、\(_8C_2×_6C_2×_4C_2×_2C_2=2520\) 通りとなります。

---

(2) は、部屋に区別のない組合せです。

例えば、次のような分け方は、(1) では別のものとして数えましたが、(2) では同じ分け方とみなします。

そのため、(1) のようにして求めた全ての分け方から、部屋の並び方による重複を取り除く必要があります。

重複しているのは4つの部屋の並び順（\(4!\) 通り）なので、(1) の結果を \(4!\) で割ります。

したがって、\(\displaystyle\frac{_8C_2×_6C_2×_4C_2×_2C_2}{4!}=105\) 通りとなります。

---

(3) は、部屋に区別のある組合せです。

まず、部屋Aに入る3人の組合せは \(_8C_3\) 通りです。

その組合せそれぞれに対して、部屋Bに入る3人の組合せは \(_5C_3\) 通り。

さらに、残った2人が部屋Cに入るため、その組合せは \(_2C_2\) 通りです。

したがって、\(_8C_3×_5C_3×_2C_2=560\) 通りとなります。

---

(4) は、3人組どうしには区別がない組合せです。

ただし、3人組と2人組は区別できます。

(3) ではAの部屋・Bの部屋と分けて考えていましたが、(4) ではその2つを同じ扱いにします。

したがって、(3) の結果から
3人組の並び順による重複（\(2!\) 通り）を取り除きます。

よって、\(\displaystyle\frac{_8C_3×_5C_3×_2C_2}{2!}=280\) 通りとなります。

まとめ：区別のない組合せ

---

---