
今日の板書はこれ!
事象A,Bが同時にはおこらないとき、つまり\(A\cap B=\emptyset\)のとき、事象A,Bは互いに排反であるという。
事象A,Bが互いに排反であるとき、確率の加法定理が成り立つ
\(P(A\cap B)=P(A)+P(B)\)
(AまたはBの確率)=(Aの確率)+(Bの確率)

もっと詳しく願いします!!
現役教員として数学を教えている「さん」と申します。
「人より勉強に時間がかかる」と感じていませんか?
私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。
• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」
• 「解答の意味が理解できず、勉強が進まない」
教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。
でも大丈夫!
このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。
意味から理解し、噛み砕き方をマスターしましょう!!
確率の加法定理
例題で考える

次の例題で考えよう!
赤玉4個、白玉3個の入った袋から2個の玉を同時に取り出すとき、2個が同じ色である確率を求めよ。
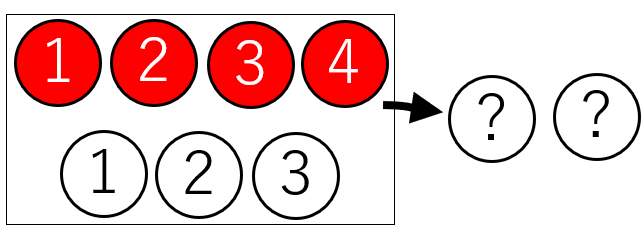
「取り出した2個の玉が同じ色である」という事象は、次の2つに分けて考えることができます。
- 「2個とも赤である」
- 「2個とも白である」
今回は、この「2個とも赤である確率」と「2個とも白である確率」をそれぞれで考えてみましょう。
全事象を考える
まずは「全事象を何にするか」を決めましょう。

なにがいいかな?

んー、「7個の玉から2個を選ぶ組合せ」かな!
分母分子の要素数を考える
次に、分母と分子の要素数を求めていきます。
分母:「7個の玉から2個を選ぶ」
分母「赤玉4個、白玉3個の入った袋から2個の玉を同時に取り出す組合せ」は\(_7C_2\)通りです。

分子:「2個とも赤を選ぶ」
「赤玉4個から2個を取り出す組合せ」は、\(_4C_2\)通り。

したがって、「2個とも赤である確率」は、\(\displaystyle \frac{_4C_2}{_7C_2}\)
分子:「2個とも白を選ぶ」
「白玉3個から2個を取り出す組合せ」は、\(_3C_2\)通り。

したがって、「2個とも白である確率」は、\(\displaystyle \frac{_3C_2}{_7C_2}\)
確率を求める

さて問題です!「2個とも赤の確率\(\displaystyle \frac{_4C_2}{_7C_2}\)」と「2個とも白の確率\(\displaystyle \frac{_3C_2}{_7C_2}\)」は、足すのでしょうか?掛けるのでしょうか?

え…足すのかな?掛けるのかな?
学校で教えていると、「確率を足すのか掛けるのか」で迷う生徒がとても多いです。
ここで一度、自分が何を求めているのか整理しましょう。
今回の問題は「取り出した2個が同じ色である確率」。
これは「2個とも赤である」か「2個とも白である」かのどちらかでOKです。
つまり、「どちらの場合でもいい」=どちらかが起こればよい
ということ。
「取り出した2個が同じ色である確率」は「2個とも赤」でもいいし、「2個とも白」でもOKです。
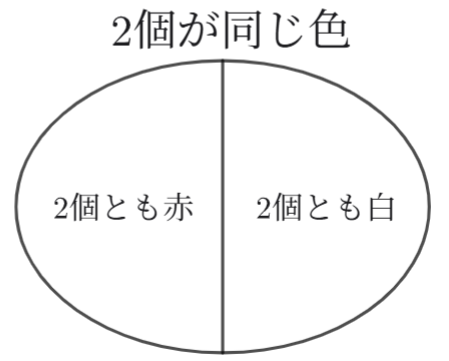
このようなときは、、確率を足します。
よって求める確率は、\(\displaystyle \frac{_4C_2}{_7C_2}+\frac{_3C_2}{_7C_2}=\frac{4\cdot 3}{7\cdot 6}+\frac{3\cdot 2}{7\cdot 6}=\frac{3}{7}\)
和の法則を使った求め方
確率の加法定理を使わずに求めてみましょう。
分母「赤玉4個、白玉3個の入った袋から2個の玉を同時に取り出す組合せ」は\(_7C_2\)
分子「取り出した2個が同じ色である組合せ」は「2個とも赤」の\(_4C_2\)通りと、「2個とも白」の\(_3C_2\)通りの合計\(_4C_2+_3C_2\)
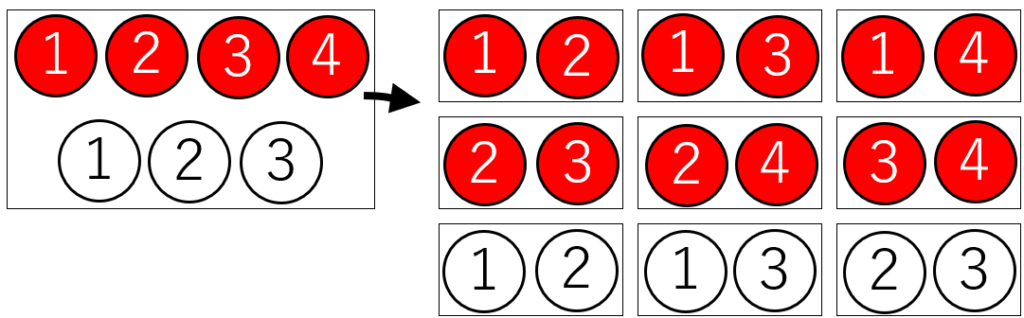
よって求める確率は、\(\displaystyle \frac{_4C_2+_3C_2}{_7C_2}=\frac{4\cdot 3 + 3\cdot 2}{7\cdot 6}=\frac{18}{7\cdot 6}=\frac{3}{7}\)

和の法則も加法定理も似たようなもんだね。

場合の数を足すのか確率を足すのかの違いだね!
確率の加法定理が使えない確率
1から30までの30枚の番号札から1枚引くとき、その番号が2の倍数または3の倍数である確率を求めよ。
事象「引いた1枚の番号が2の倍数または3の倍数」次の2つの事象に分けて考えられます。
- 「2の倍数である」
- 「3の倍数である」
全事象を考える
まずは、「全事象を何にするか」を決めていきます。

なにがいいかな?

30枚の札から1枚を選ぶ組合せ!!
分母分子の要素数を考える
次に、分母分子の要素数を求めていきます。
分母:「30枚の札から1枚を選ぶ」
分母「30枚の番号札から1枚の選び方」は\(30\)通り。
分子:「2の倍数」
「2の倍数」は\(30÷2=15\)より\(15\)通り。
よって、「2の倍数の確率」は、\(\displaystyle \frac{15}{30}\)
分子:「3の倍数」
「3の倍数」は\(30÷3=10\)より\(10\)通り。
よって、「3の倍数の確率」は、\(\displaystyle \frac{10}{30}\)
確率を求める

さて問題です!「2の倍数の確率\(\frac{15}{30}\)」と「2個とも白の確率\(\frac{10}{30}\)」は、足す?それとも掛ける?

さっきと同じ!足す!!

ちょっと意地悪だったね。今回は単純に足してはいけないんだ。

なぬ!?
「2の倍数または3の倍数の確率」は「2の倍数の確率」と「3の倍数の確率」をそのまま足しても求まりません。
なぜなら、2つの事象が同時に起こる場合があるからです。
このような場合、「加法定理」がそのまま使えないのです。
加法定理が使えるのは、事象AとBが同時には起こらない(=排反)ときだけ。
今回、「6の倍数」であるとき、「2の倍数である」と「3の倍数である」が同時に成立してしまいます。
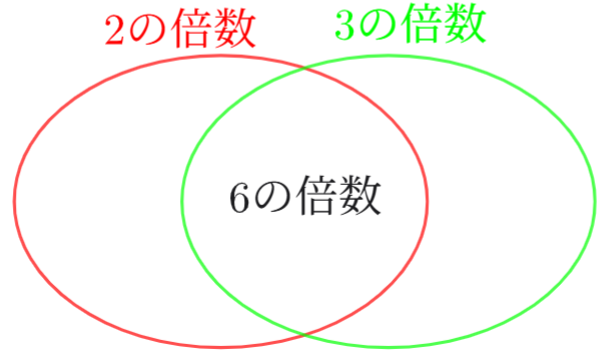
この重なりの部分を引いてあげることで、正しい確率が求められます。
6の倍数は\(30÷6=5\)より\(5\)通りであるから、6の倍数の確率は\(\displaystyle \frac{5}{30}\)
したがって、、\(\displaystyle \frac{15}{30}+\frac{10}{30}-\frac{5}{30}=\frac{2}{3}\)

なるほど!場合の数でも「重なりを引く」ってやったよね!

その通り!確率も同じで、重なりを引くのがポイントなんだ。
まとめ:確率の加法定理

さて、今回のまとめだよ!
事象A,Bが同時にはおこらないとき、つまり\(A\cap B=\emptyset\)のとき、事象A,Bは互いに排反であるという。
事象A,Bが互いに排反であるとき、確率の加法定理が成り立つ
\(P(A\cap B)=P(A)+P(B)\)
(AまたはBの確率)=(Aの確率)+(Bの確率)

ありがとうございました!!






コメント