
今日の板書はこれ!
「どの事象が何回起これば目的の状態になるか」を考え、その回数に対応する反復試行の確率を求める。

もっと詳しく願いします!!
現役教員として数学を教えている「さん」と申します。
「人より勉強に時間がかかる」と感じていませんか?
私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。
• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」
• 「解答の意味が理解できず、勉強が進まない」
教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。
でも大丈夫!
このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。
意味から理解し、噛み砕き方をマスターしましょう!!
反復試行による直線上の点の移動
例題

次の例題で考えよう!
数直線上を動く点Pが原点の位置にある。1枚の硬貨をなげて、表が出たときにはPを正の向きに2だけ進め、裏が出たときはPを負の向きに1だけ進める。硬貨を6回投げ終わったとき、Pが原点に戻っている確率を求めよ。
「硬貨を6回投げる」という同じ条件の試行を繰り返しているので、これは反復試行の問題です。
表が出たときは座標が\(+2\)、裏が出たときは座標が\(−1\)動きます。
原点に戻るときのパターンを考える
6回投げたあとにPが原点に戻っているのは、たとえば[表,表,裏,裏,裏,裏]や[表,裏,裏,裏,表,裏]のような場合です。
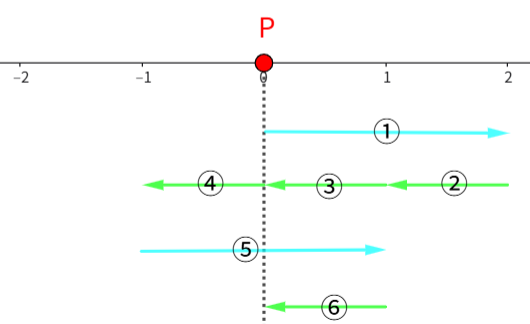
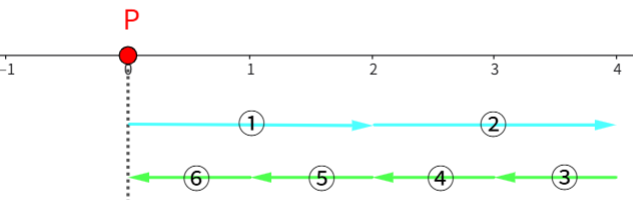
このことから、表が2回、裏が4回出るときに点Pは原点に戻ることがわかります。

これを計算で求めよう!
計算で確認してみよう
表が出る回数を\(x\)とすると、移動後の座標は\( \color{Blue}{(+2)×x}+ \color{green}{(-1)×(6-x)}=\color{red}{3x-6}\)と表せます。
これが原点(0)になるとき、\(\color{red}{3x-6=0}\)より\(\color{red}{x=2}\)
やはり、表が2回のときにPは原点に戻ります。

最後に確率を求めておしまいだよ!
確率の計算
表が2回、裏が4回出る確率は、
\(\displaystyle\color{red}{_6C_2}× \color{Blue}{\left(\frac{1}{2}\right)^2}× \color{green}{\left(\frac{1}{2}\right)^4}=\frac{15}{64}\)
まとめ:反復試行による直線上の点の移動

さて、今回のまとめだよ!
「どの事象が何回起これば目的の状態になるか」を考え、その回数に対応する反復試行の確率を求める。

ありがとうございました!!






コメント