今日の板書はこれ！
\(h ≒ 0 \) のとき \(\color{hotpink}{f(a+h)} ≒ \color{springgreen}{f(a)} + \color{deepskyblue}{f'(a)h}\)
\(x ≒ 0 \) のとき \(f(x) ≒ \color{gold}{f(0)} + \color{red}{f'(0)x}\)
詳しく願いします m(_ _)m
「人より勉強に時間がかかる」と感じていませんか？
私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。
• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」
• 「解答の意味が理解できず、勉強が進まない」
教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。
でも大丈夫！
このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。
「噛み砕き方」がわかれば、文章はぐっと読みやすくなります！
頑張っているのに、なかなか成績が上がらなくて、苦しんでる方へ。
画像をクリックして、記事を読んでみて。
きっと力になるはず。
近似式とは
今回は「近似式」を扱っていくよ！
近似式？何それ？
「近似式」とは「本当の式の代わりにする、だいたい同じ式のこと」です。
例えば、\(\sqrt{2} ≒ 1.41\) も近似式。
ほんとは、\(\sqrt{2} = 1.4142135623•••\) と無限に続くのですが、
近似式を用いると、式を簡単にしたり、だいたいの値を表現することができます。
「近似した式」で近似式か。そのままだね。
高校では２つの近似式を使えればOK！
近似式の公式①：\(f(a+h) ≒ f(a) + f'(a)h\)
\(h ≒ 0 \) のとき \(\color{hotpink}{f(a+h)} ≒ \color{springgreen}{f(a)} + \color{deepskyblue}{f'(a)h}\)
まずは、公式①の「使い方」と「成り立つ理由」について説明していきます。
次の例題で、近似式①の使い方を学ぼう！
使い方
\(\sin{31°}\) を求めよ。
えっ、\(\sin{31°}\) ？
\(\sin{30°}\) ならわかるけど•••。
おっ。いいところに気づいたね！
「\(\color{hotpink}{f(a+h)} ≒ \color{springgreen}{f(a)} + \color{deepskyblue}{f'(a)h}\)」は、
「\(\color{hotpink}{f(a+h)}\)は 、\(h\) がほとんど \(0\) に近かったら \(\color{springgreen}{f(a)} + \color{deepskyblue}{f'(a)h}\) とほぼ一緒」という意味です。
この近似式①を使って、\(\sin{31°}\) を考えます。
\(\sin{31°}\) を \(\sin{(30°+1°)}\) と考えると、
「\(\color{hotpink}{\sin{(30°+1°)}}\) は 、\(1°\) がほとんど \(0\) に近いので \( \color{springgreen}{\sin{30°}} + \color{deepskyblue}{(\sin{30°})’ \cdot 1° }\) とほぼ一緒」
と考えることができます。
弧度法に直すと、
\(\displaystyle\color{hotpink}{\sin{(30°+1°)}} = \color{hotpink}{\sin{\left(\frac{\pi}{3}+\frac{\pi}{180}\right)}}\)
ですから、
これを計算すると、
となります。
ほー。こんな使い方をするのか。
近似式を使うと、値を知ってる関数の付近であれば、計算することができるんだ！
成り立つ理由
使い方はわかったけど、この近似式が成り立つ理由が気になる。
そうだよね。次のグラフを使って説明していくよ。
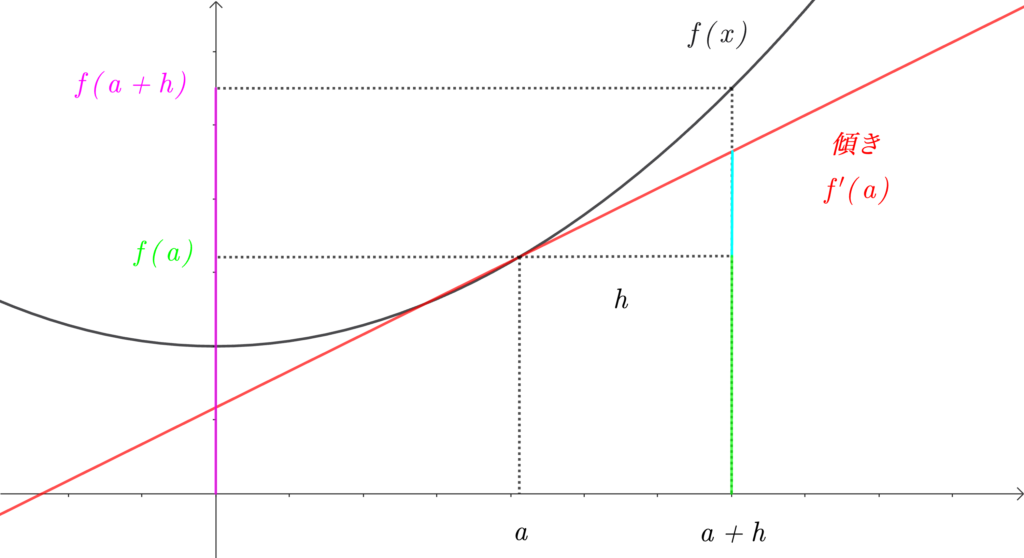
\(h ≒ 0 \) のとき \(\color{hotpink}{f(a+h)} ≒ \color{springgreen}{f(a)} + \color{deepskyblue}{f'(a)h}\) が成り立つ理由を説明します。
簡単にいうと、
「\(\color{hotpink}{f(a+h)}\) の長さ」は、「\(\color{springgreen}{f(a)}\) に\(\color{deepskyblue}{f'(a)h}\) を加えた長さ」とほとんど同じ
ということです。
まあ•••見た目的にはほとんど一緒だけれども。
大丈夫！詳しく説明するよ！
１つずつ丁寧に説明していきます。
まず、\(\color{springgreen}{f(a)}\) と \(\color{hotpink}{f(a+h)}\) は、下の図の緑とピンクの長さです。
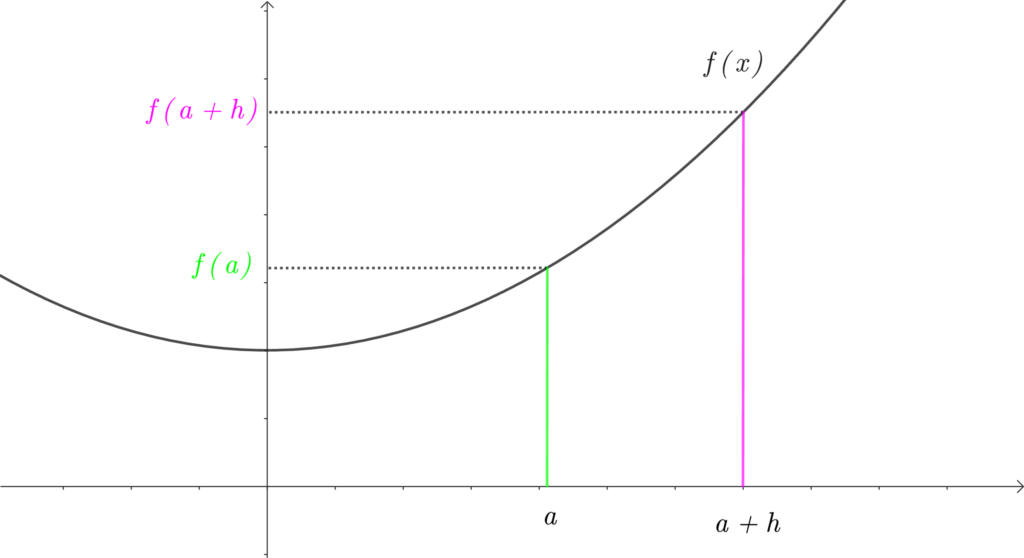
\(\color{springgreen}{f(a)}\) の長さと \(\color{hotpink}{f(a+h)}\) の長さの間には、まだ差があります。
この図だと半分くらい違うね。
そこで、\(\color{springgreen}{f(a)}\) の長さに、少しだけプラスして、\(\color{hotpink}{f(a+h)}\) の長さと同じくらいにしていきます。
そのプラス分が、\(\color{deepskyblue}{f'(a)h}\) です。
\(\color{deepskyblue}{f'(a)h}\) 下の図の水色の長さです。
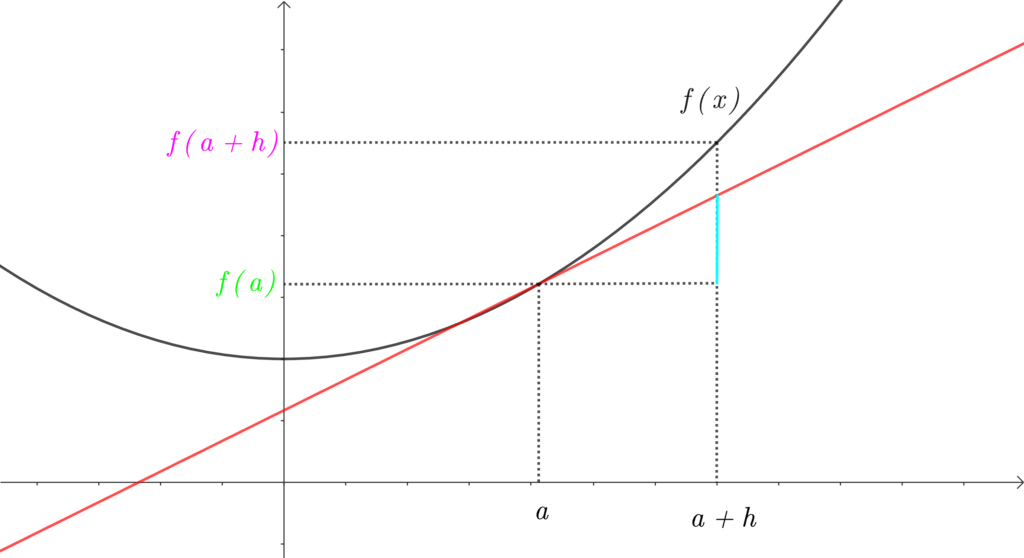
まだ、よくわかりませんね。
もう少し説明します。
よろしくお願いします！
\(\color{red}{f'(a)}\) は、下の図の接線の傾きです。
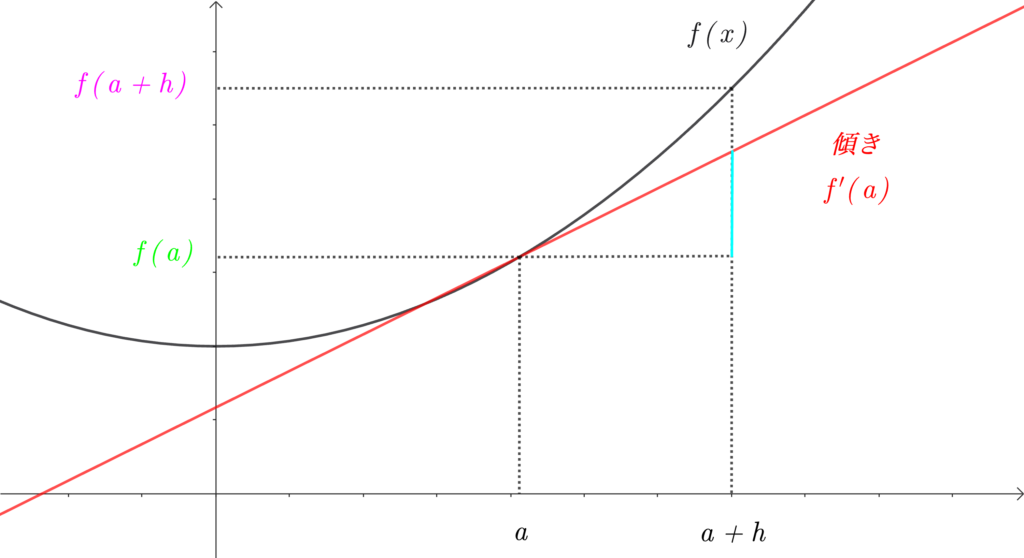
\(h\) は \(a\) から \(a+h\) までの長さであり、
\(\color{red}{f'(a)}=\frac{\color{deepskyblue}{(水色の長さ)}}{h}\) であるので、
\(\color{red}{f'(a)}\) に \(h\) を掛けた \(\color{deepskyblue}{f'(a)h}\) は、
水色の長さになる というわけです。
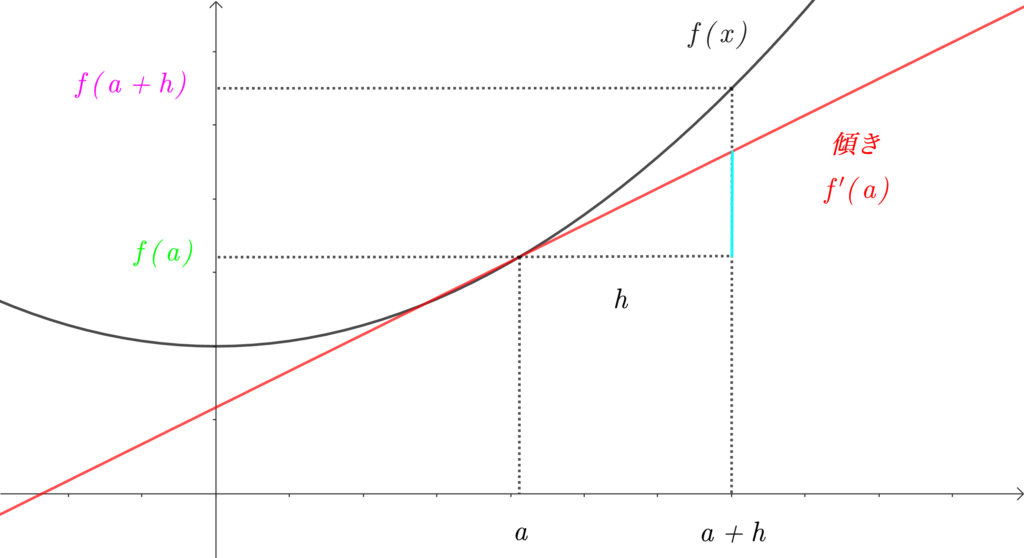
では、「\(\color{hotpink}{f(a+h)}\) の長さ」と、「\(\color{springgreen}{f(a)}\) に \(\color{deepskyblue}{f'(a)h}\) を加えた長さ」をもう一度見比べてみましょう。
「\(\color{hotpink}{f(a+h)}\) の長さ」は、「\(\color{springgreen}{f(a)}\) に \(\color{deepskyblue}{f'(a)h}\) を加えた長さ」と、ほとんど同じですね。
そして、\(h\) がほとんど \(0\) のとき、その差はもっと小さくなります。
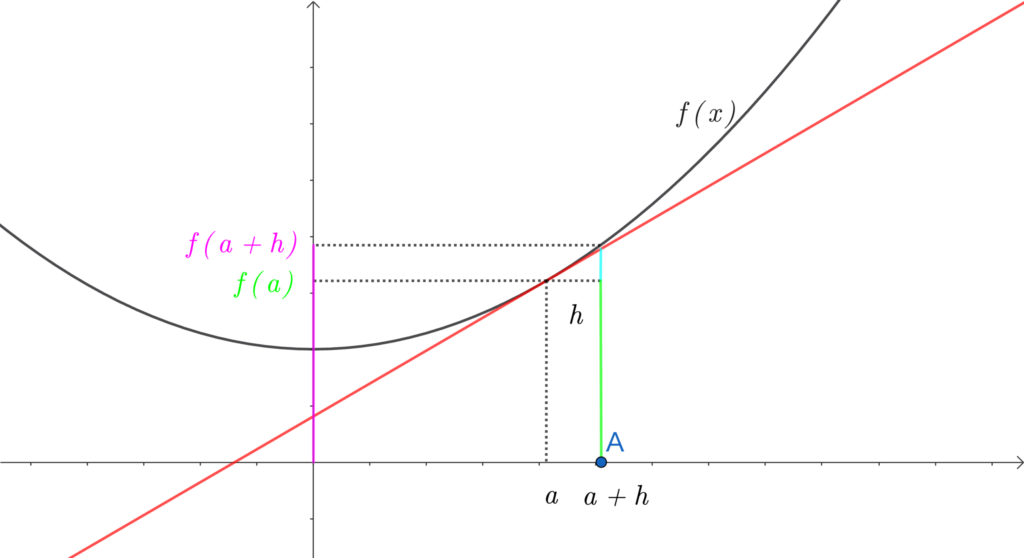
ですから、
\(h ≒ 0 \) のとき \(\color{hotpink}{f(a+h)} ≒ \color{springgreen}{f(a)} + \color{deepskyblue}{f'(a)h}\) が成り立つ
というわけです。
理解できたかな？
近似式の公式②： \(f(x) ≒ f(0) + f'(0)x\)
\(x ≒ 0 \) のとき \(f(x) ≒ \color{gold}{f(0)} + \color{red}{f'(0)x}\)
近似式②の「使い方」と「成り立つ理由」について説明していきます。
まずは次の例題で、使い方を学ぼう！
使い方
\(r\) を実数とする。\(x ≒ 0 \) のとき、\((1+x)^r ≒ 1+rx\) であることを示せ。また、この式を用いて \(\sqrt[4]{1.008}\) の近似値を求めよ。
\(f(x) ≒ \color{gold}{f(0)} + \color{red}{f'(0)x}\) を使って \((1+x)^r ≒ 1+rx\) を示そう！
証明って苦手意識あるな･･•。
\(f(x) ≒ \color{gold}{f(0)} + \color{red}{f'(0)x}\) が成り立つことを使います。
まずは、\(f(x)\) を設定するところから。
\(f(x)=(1+x)^r \) とする。
次に、\(\color{gold}{f(0)}\) と \(\color{red}{f'(0)}\) を準備します。
\(\color{gold}{f(0)}=(1 + 0 )^r = \color{gold}{1}\)
\(f'(x) = r(1 + x )^{r-1}\) であるから、 \(\color{red}{f'(x)} = r(1 + 0 )^{r-1}=\color{red}{r}\)
最後に、\(f(x) ≒ \color{gold}{f(0)} + \color{red}{f'(0)x}\) を立式しておしまいです。
よって \(x ≒ 0 \) のとき、\((1+x)^r ≒ \color{gold}{1} + \color{red}{rx}\)
あれ、意外に簡単。
次は、\(\sqrt[4]{1.008}\) の近似値を求めよう！
\(\sqrt[4]{1.008}\) の値を直接計算することはできません。
そこで、 \((1+x)^r ≒ \color{gold}{1} + \color{red}{rx}\) を使って近似値を求めます。
まずは、\(\sqrt[4]{1.008}\) を \((1+x)^r\) の形に変形します。
\(\sqrt[4]{1.008} = (1+0.008)^{\frac{1}{4}}\)
\(r\) を \(\frac{1}{4}\) に置き換え、
\(0.008≒0\) ですから \(x\) を \(0.008\) に置き換えると
おお！こんな感じで求めれるのか！
成り立つ理由
この近似式が成り立つ理由も教えて！
了解！次の図で説明していくね。
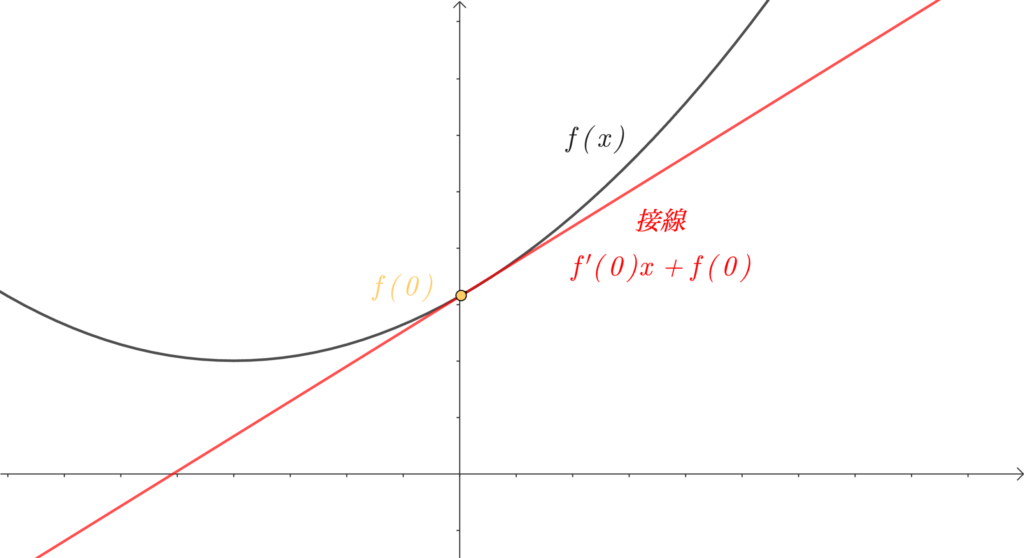
上の図では２つの関数があります。
１つ目は \(f(x)\)。
2つ目は \(f'(0)x + f(0)\)。
\(f'(0)x + f(0)\) は、\(f(x)\) 上の点 \(\color{gold}{(0, f(0)}\) を通る、接線の方程式です。
※接線の方程式がわからない方はこちら↓
微分法の応用01:「接線の方程式と法線の方程式」
この２つの関数の \(x\) が \( 0 \) の付近を見比べてみてください。
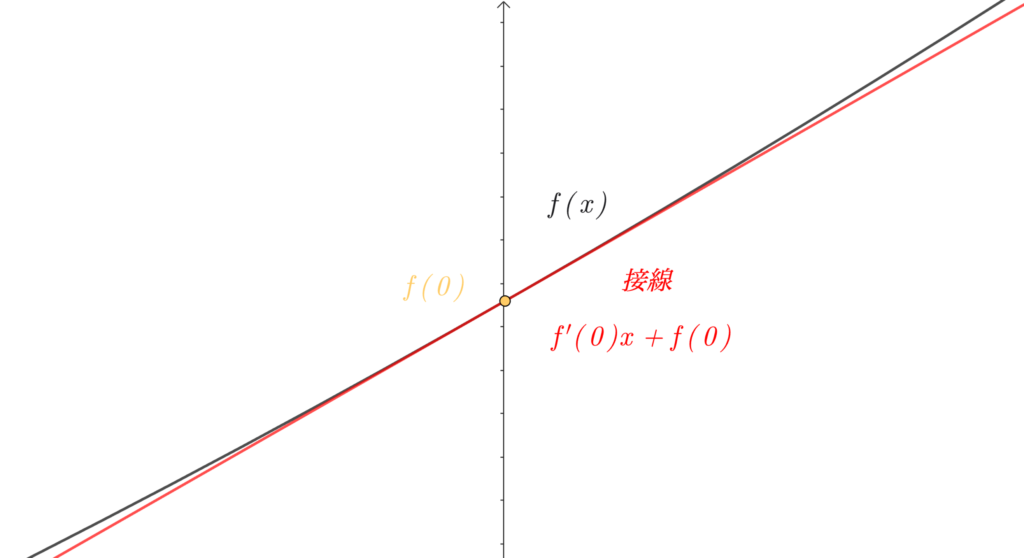
あ、ほとんど一緒だ。
そういうこと！
\(f(x) ≒ \color{gold}{f(0)} + \color{red}{f'(0)x}\) は、
「\(x ≒ 0 \) のとき 関数\(f(x)\) と 関数\(\color{red}{f'(0)x+\color{gold}{f(0)} }\) はほとんど同じだよね」って公式なんです。
理解したら、単純なことだった！
まとめ
さて、今回のまとめだよ！
\(h ≒ 0 \) のとき \(\color{hotpink}{f(a+h)} ≒ \color{springgreen}{f(a)} + \color{deepskyblue}{f'(a)h}\)
\(x ≒ 0 \) のとき \(f(x) ≒ \color{gold}{f(0)} + \color{red}{f'(0)x}\)
\(\sin{31°}\) を求めよ。
\(r\) を実数とする。\(x ≒ 0 \) のとき、\((1+x)^r ≒ 1+rx\) であることを示せ。また、この式を用いて \(\sqrt[4]{1.008}\) の近似値を求めよ。
\(f(x)=(1+x)^r \) とする。
\(\color{gold}{f(0)}=(1 + 0 )^r = \color{gold}{1}\)
\(f'(x) = r(1 + x )^{r-1}\) であるから、 \(\color{red}{f'(x)} = r(1 + 0 )^{r-1}=\color{red}{r}\)
よって \(x ≒ 0 \) のとき、\((1+x)^r ≒ \color{gold}{1} + \color{red}{rx}\)
また、
これで「微分法の応用」の単元全部終わった！！
頑張っているのに、なかなか成績が上がらなくて、苦しんでる方へ。
画像をクリックして、記事を読んでみて。
きっと力になるはず。
↑前の記事↑
↑まとめ記事↑
コメント