【教科書が読めるようになる数Ⅲ】漸近線の種類

さん

こんにちは、高校教員の『さん』です。今日は、「グラフの漸近線」について詳しく説明していくよ。

生徒

今回もよろしくお願いします！！

「人より勉強に時間がかかる」と感じていませんか？

私のクラスにも、同じ悩みを抱えて苦しんでいた生徒がたくさんいました。

• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」

• 「解答の意味が理解できず、勉強が進まない」

教科書の内容を理解するには、「自分で噛み砕いて考える力」が必要です。

このブログでは、よく寄せられる質問、つまずきやすいポイントをもとに、教科書の内容をわかりやすく解説していきます。

「噛み砕き方」がわかれば、文章はぐっと読みやすくなります！

まずは、教科書の説明を見てみましょう。

まずは教科書の説明
簡単に説明するよ
詳しく説明するよ
1. 漸近線を考える
まとめ

まずは教科書の説明

さん

教科書の説明ではこんなふうに書かれているよ！

例題

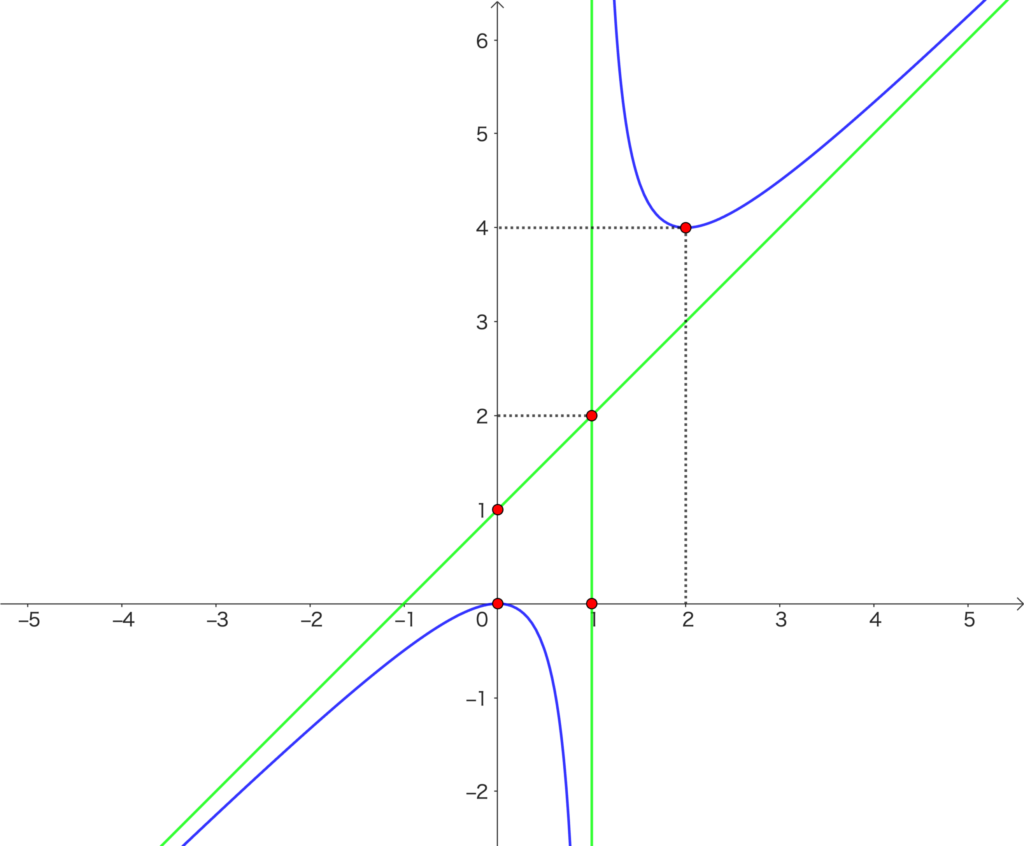
関数 \(y=\frac{x^2}{x-1}\) のグラフをかけ。

関数の定義域は \(x\neq1\) である。

\(f(x) = \frac{x^2}{x-1}\) とする。

\(f(x) = x + 1 + \frac{1}{x-1}\) であるから

\(f'(x) = 1 – \frac{1}{({x-1})^2}=\frac{x(x-2)}{({x-1})^2}\)

\(f(x)^{\prime\prime} = \frac{2}{({x-1})^3}\)

\(f(x)\) の増減や凹凸は、次の表のようになる。

\( \begin{array}{c|ccccccc} x & \cdots & 0 & \cdots & 1 & \cdots & 2 & \cdots \\ \hline y’ & + & 0 & – & \text{／} & – & 0 & + \\ \hline y^{\prime\prime} & – & – & – & \text{／} & + & + & +\\ \hline y & \text{上に凸に}\nearrow & 0 & \text{上に凸に}\searrow & \text{／} & \text{下に凸に}\searrow　& 4 & \text{下に凸に}\nearrow \end{array} \)

また、\(\displaystyle\lim_{n \to 1 + 0} f(x) = \infty\)、\(\displaystyle\lim_{n \to 1 – 0} f(x) = -\infty\)であるから、\(x=1\) はこの曲線の漸近線である。

さらに、\(\displaystyle\lim_{n \to \infty} \{f(x) – (x + 1)\} = 0\)、\(\displaystyle\lim_{n \to -\infty} \{f(x) – (x + 1) \}= 0\) であるから、直線 \(y = x + 1\) もこの曲線の漸近線である。

以上から、グラフは下の図のようになる。

簡単に説明するよ

漸近線の種類は次の３つ

\(y = a\) 型の横の漸近線
\(x = a\) 型の縦の漸近線
\(y = ax + b\) 型の斜めの漸近線

です。

生徒

メモメモ•••

詳しく説明するよ

グラフをかくときの、気をつけるべき漸近線の種類について説明していきます。

例題

関数 \(y=\frac{x^2}{x-1}\) のグラフをかけ。

生徒

グラフのかき方については前回、勉強したよ！

さん

漸近線を考えるとこまでは、軽く振り返りながらやっていこう！

ラフのかき方は、

定義域を確認する
微分計算により \(y’\) や \(y^{\prime\prime}\) を計算する
\(y’=0\)、 \(y^{\prime\prime} = 0\) を求め増減表を作る
漸近線があれば図示する
グラフをかく

でした。

生徒

定義域は絶対最初に確認しないといけなかったんだよね！

さん

よく覚えていたね！確認ポイントは次の３つ！

定義域の主な確認ポイント

①（分母）\(\neq 0\)
② \(\sqrt{\text{0以上}}\)
③ \(\log{\text{(正)}}\)

今回の関数 \(y=\frac{x^2}{x-1}\) は分数関数なので、（分母）\(\neq 0\) を確認します。

\(x -1 \neq 0\) より定義域は \(x \neq 1\)

生徒

次は\(y’\) や \(y^{\prime\prime}\) を計算するんだったね。

さん

分数関数のグラフを図示する上で、次の変形は必須なんだ。覚えておこうね。

分数関数の微分ポイント

(分子の次数) ≧ (分母の次数)であれば、分子の次数を分母の次数より小さくする。

（分子 \(x^2\) の次数 \(2\)） ≧ （分母 \(x-1\) の次数 \(1\)）ですから、次の変形をします。

\begin{align*} \require{enclose} % enclose 拡張機能を用いて % \enclose{longdiv} で筆算の除算記号が表示可能 x + 1 \phantom{+ 0} \\ x – 1 \enclose{longdiv}{ x^2 \phantom{+x}} \phantom{+ 0} \\ \underline{ x^2 – x } \phantom{ + 0 } \\ {} x \phantom{ + 0} \\ \underline{ {} x – 1 } \\ 1 \end{align*}

筆算より、\(x^2 = (x-1)(x+1)+1\) とできることを利用して

\( \begin{aligned} \displaystyle y &= \color{red}{\frac{x^2}{x-1}} \\ \text{} \\ &= \frac{(x-1)(x+1)+1}{x-1} \\ \text{} \\ &= \color{red}{x + 1 + \frac{1}{x-1}} \\ \text{} \\ \end{aligned} \)

と変形します。

これで、分子の次数が分母の次数より小さくなりました。

生徒

なんでこの変形をしないといけないの？

さん

微分も簡単にできるし、漸近線を描くためにも必要なんだ！

\(y= x + 1 + \frac{1}{x-1}\) を微分します。

\( \begin{aligned} \displaystyle y’ &= 1 – \frac{1}{({x-1})^2} \\ \text{} \\ &= \frac{({x-1})^2-1}{({x-1})^2} \\ \text{} \\ &= \frac{x^2-2x}{({x-1})^2} \\ \text{} \\ &= \frac{x(x-2)}{({x-1})^2} \\ \text{} \\ \end{aligned} \)

生徒

因数分解するところまで、計算するんだったね！

次に、\(y^{\prime\prime}\) を計算していくのですが、一番計算が楽な \(y’ = 1 – \frac{1}{({x-1})^2}\) を微分しましょう。

\(\displaystyle y^{\prime\prime} = \frac{2}{({x-1})^3}\)

さん

次は、\(y’=0\)、 \(y^{\prime\prime} = 0\) を求めて増減表を作ろう！

\(y’=0\) とすると \(x=0, 2\)

\(y^{\prime\prime} = 0\) になることはありません。

増減表は、定義域も考慮してかきます。

定義域に含まれていない \(x = 1 \) には「／」をかき入れておきましょう。

漸近線を考える

さん

ここからが、本番！漸近線の種類を説明していくよ。

漸近線①：\(y = a\) 型の横の漸近線

生徒

横の漸近線は、前回でもやった気がする。

さん

グラフの端っこがどうなってるか確認するんだったね！

\(y= x + 1 + \frac{1}{x-1}\) の極限を考えます。

\( \begin{aligned} \displaystyle \lim_{n \to \infty} \left( x + 1 + \frac{1}{x-1} \right) &= \infty + 1 + 0 \\ \text{} \\ &= \infty \\ \text{} \\ \end{aligned} \)

\( \begin{aligned} \displaystyle \lim_{n \to -\infty} \left( x + 1 + \frac{1}{x-1} \right) &= -\infty + 1 + 0 \\ \text{} \\ &= -\infty \\ \text{} \\ \end{aligned} \)

右端は \(\infty\) に上がっていき、左端は \(-\infty\) に下がっていくので、\(y = a\)型の横の漸近線はありませんでした。

さん

これは頭の中で考えればOK。解答には記述する必要はないよ

漸近線②：\(x = a\) 型の縦の漸近線

生徒

縦の漸近線もあるんだ。

さん

\(x = a\) 型の縦の漸近線は次の３つが存在する場合に考えよう！

\(x = a\)型の縦の漸近線を考えるポイント

①（分母）\(\neq 0\)が絡む
② \(\sqrt{\text{0以上}}\)が絡む
③ \(\log{\text{(正)}}\)が絡む

生徒

あれ、これって定義域の確認ポイントと一緒？

さん

そうだね！定義域の範囲があるときは、\(x = a\) 型の縦の漸近線も考えることを忘れないようにね！

定義域の端っこがどうなってるかを考えましょう。

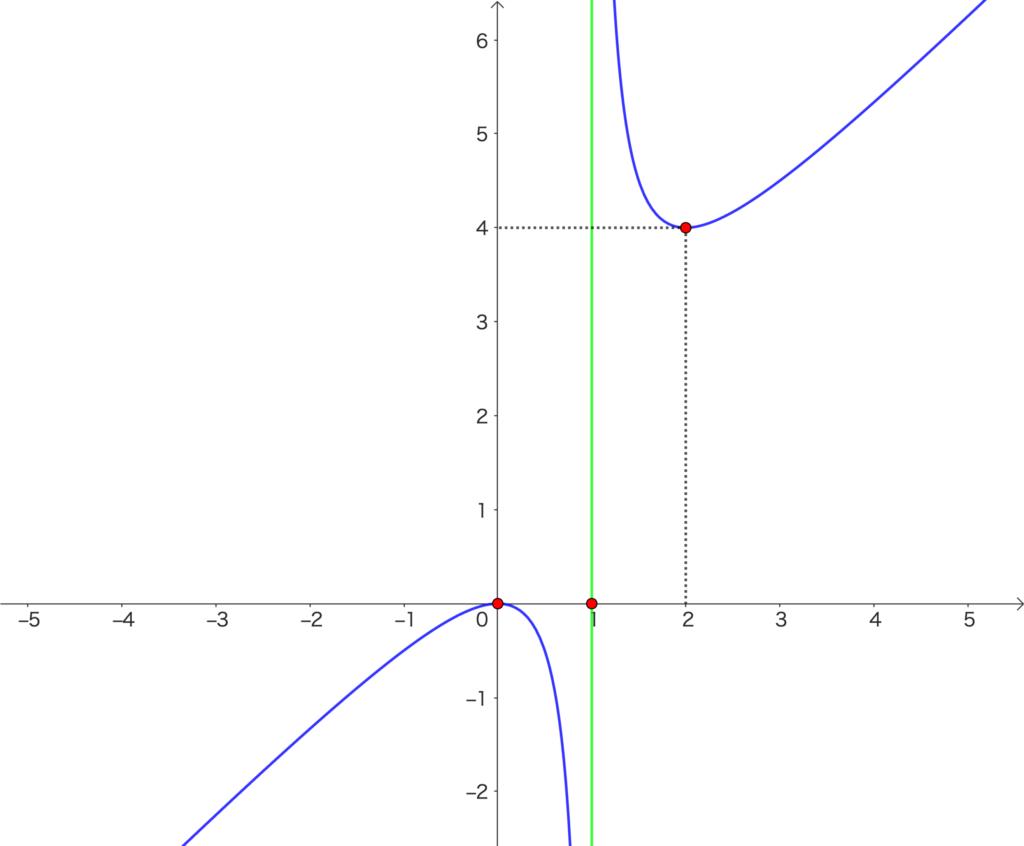
定義域は \(x \neq 1\) でしたので、関数\(y= \frac{x^2}{x-1}\) が \(x = 1\)に近づくとき、グラフはどうなるかを考えます。

まずは、右から近づくとき。

\(\displaystyle\lim_{n \to 1 + 0} \frac{x^2}{x-1}= \infty\)

次に、左から近づくとき。

\(\displaystyle\lim_{n \to 1 – 0} \frac{x^2}{x-1} = -\infty\)

さん

これで、\(x=1\) はこの曲線の漸近線だって言えるようになったね！

漸近線③：\(y = ax + b\) 型の斜めの漸近線

生徒

斜めの漸近線もあるんだ•••。大変。

さん

大丈夫！次のことを覚えておけばすぐに判断できるよ！

\(y = ax + b\)型の斜めの漸近線を考えるポイント

① 分数関数である。
→ （1次式）＋（分数関数）のグラフは \(y = \) （1次式）が漸近線になる。
② 無理数関数である。

生徒

さっき、分数関数を変形したのはここで使うからか！

さん

その通り！鋭いね！

（1次式）＋（分数関数）のグラフは \(y = \)（1次式）が漸近線になります。

今回の関数は \(y = \frac{x^2}{x-1} = \color{red}{x + 1 + \frac{1}{x-1}}\) ですから、\(\color{red}{y = x + 1}\)が漸近線になります。

これを、知識として分かっている上で、解答としても \(\color{red}{y = x + 1}\) が漸近線であることを示しておきましょう。

\(y = x + 1\)が漸近線であるということは、

「関数 \(\color{hotpink}{y = \frac{x^2}{x-1}}\) が \(\color{deepskyblue}{y = x + 1}\) にどんどん近づいていく」ということでした。

つまり、「\(\color{hotpink}{y = \frac{x^2}{x-1}}\) と \(\color{deepskyblue}{y = x + 1}\) との差 \(\color{hotpink}{\frac{x^2}{x-1}} – \color{deepskyblue}{(x + 1)}\) がだんだん0に近づいていく」ということです。

これを式で表してあげましょう。

\( \begin{aligned} \displaystyle \lim_{n \to \infty} \left(\color{hotpink}{\frac{x^2}{x-1}} – \color{deepskyblue}{(x + 1)}\right) &= \lim_{n \to \infty} \left(\color{hotpink}{\left(x + 1 + \frac{1}{x-1}\right)}-\color{deepskyblue}{(x + 1)}\right) \\ \text{} \\ &= \lim_{n \to \infty} \frac{1}{x-1} \\ \text{} \\ &= 0 \\ \text{} \\ \end{aligned} \)

よって、\(y = x + 1\)が漸近線である。

生徒

ちゃんと、解答で示さないといけないのか。

さん

誰がみても分かるように根拠を記述しないとね！

後は、漸化式、座標軸との交点、極値、変曲点などをかき入れて、グラフを完成です。

解答

定義域は \(x\neq1\)

\(f(x) = \frac{x^2}{x-1}\) とする。

\( \begin{aligned} \displaystyle f(x) &= \frac{x^2}{x-1} \\ \text{} \\ &= \frac{(x-1)(x+1)+1}{x-1} \\ \text{} \\ &= x + 1 + \frac{1}{x-1} \\ \text{} \\ \end{aligned} \)

\( \begin{aligned} \displaystyle f(x)’ &= 1 – \frac{1}{({x-1})^2} \\ \text{} \\ &= \frac{({x-1})^2-1}{({x-1})^2} \\ \text{} \\ &= \frac{x^2-2x}{({x-1})^2} \\ \text{} \\ &= \frac{x(x-2)}{({x-1})^2} \\ \text{} \\ \end{aligned} \)

\(\displaystyle f(x)^{\prime\prime} = \frac{2}{({x-1})^3}\)

\(f(x)’=0\) とすると \(x=0, 2\)

\(\displaystyle\lim_{n \to 1 + 0} \frac{x^2}{x-1}= \infty\)、\(\displaystyle\lim_{n \to 1 – 0} \frac{x^2}{x-1} = -\infty\) より、\(x=1\) が漸近線となる。

\(\displaystyle \lim_{n \to \infty} \left(f(x) – (x + 1)\right) = 0 \) より、\(y=x+1\) が漸近線となる。

まとめ

今回の内容をしっかり整理しておこう！

生徒

グラフのかき方をマスターできた気がする！

関数のグラフをかくときは、「定義域の確認」からスタート。
分数関数のグラフでは、「（1次式）＋（分数）」の形に変形。
\(y^{\prime}\)、\(y^{\prime\prime} \) を計算し、増減表を作成。
漸近線は3種類
- \(y = a\) 型の横の漸近線
- \(x = a\) 型の縦の漸近線
- \(y = ax + b\) 型の斜めの漸近線
特に、今回のような分数関数では、「\(y=ax+b\) 型の斜めの漸近線」を見逃さないように注意。