【数学Ⅰ】三角比10：余弦定理

さん

今日の板書はこれ！

余弦定理

\(a^2=b^2+c^2-2bc\cos{A}\)

\(b^2=c^2+a^2-2ca\cos{B}\)

\(c^2=a^2+b^2-2ab\cos{C}\)

例題

(1) △ABCにおいて、\(b=\sqrt{3}\) 、\(c=2\)、\(A=150°\) のとき、\(a\) を求めよ。

解答

(1) 余弦定理より

\(\color{red}{a^2}=\color{lime}{{(\sqrt{3}\:)}}^2+\color{lime}{{2\:}}^2\)
　　　　　\(-2\cdot\color{lime}{\sqrt{3}}\cdot \color{lime}{2}\cdot\color{lime}{\cos{150°}}\)
　\(=3+4-2\cdot\sqrt{3}\cdot 2\cdot\left(\frac{-\sqrt{3}}{2}\right)\)
　\(= 13\)

よって \(a>0\) より \(a=\sqrt{3}\)

(2) △ABCにおいて、\(b=\sqrt{6}\) 、\(A=45°\)、\(B=60°\) のとき、\(a\) を求めよ。

解答

(2) 余弦定理より

\(\displaystyle \cos{C}=\frac{\color{deepskyblue}{3}^2+\color{deepskyblue}{2}^2-(\color{deepskyblue}{\sqrt{7}})^2}{2\cdot \color{deepskyblue}{3}\cdot \color{deepskyblue}{2}}=\frac{1}{2}\)

よって

\(C = 60°\)

生徒

もっと詳しく願いします！！

「人より勉強に時間がかかる」と感じていませんか？

私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。

• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」

• 「解答の意味が理解できず、勉強が進まない」

教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。

でも大丈夫！

このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。

「噛み砕き方」がわかれば、文章はぐっと読みやすくなります！

勉強しても成績が上がらない3つの理由と現役教師が教えるたった1つの解決策

一生懸命やってるのに結果が出ない…そんな中高生の悩みを、現役教師が本気で解決！信頼できる家庭教師が導く正しい学び方とは？

余弦定理
まとめ：余弦定理

余弦定理

生徒

正弦定理の次は余弦定理？

さん

余弦はcosのことだよ！

余弦定理

\(a^2=b^2+c^2-2bc\cos{A}\)

\(b^2=c^2+a^2-2ca\cos{B}\)

\(c^2=a^2+b^2-2ab\cos{C}\)

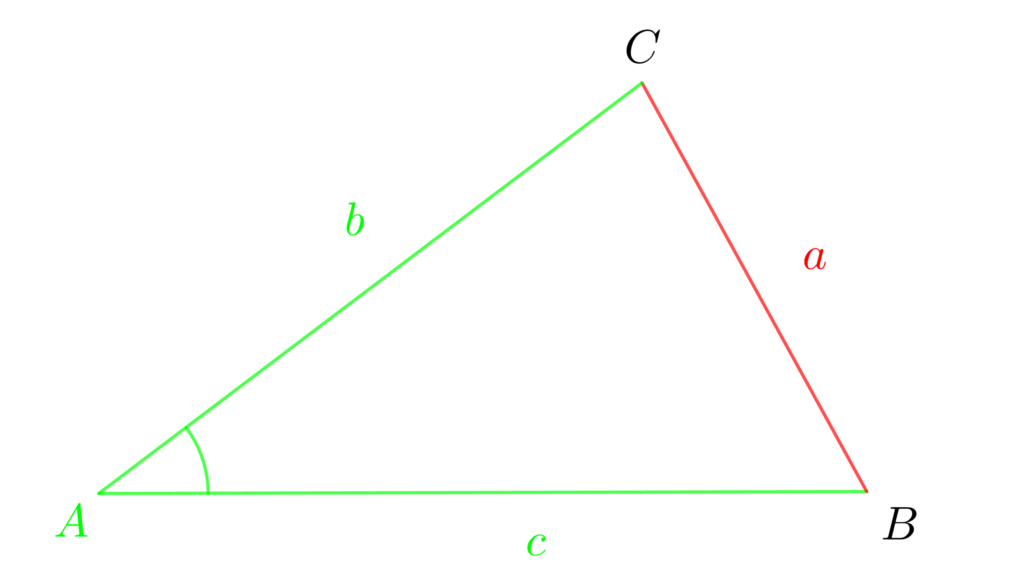
余弦定理は「隣り合う２辺とその間の角から対辺が分かる式」です。

この式をそのまま暗記するのではなく、図でイメージできるようにしておきましょう。

記事の後半で導出はしますが、余弦定理はもともと「三平方の定理」を使っています。

三平方の定理「\(a^2=b^2+c^2\)」に「\(-2bc\cos{A}\)」が加わったと考えれば、覚えやすいと思います。

余弦定理の使い方①

生徒

実際にはどうやって使うの？

さん

余弦定理は「２辺とその間の角から対辺が分かる式」だったね。

このイメージを持っていると忘れにくくなり、どんな時に余弦定理を使えばいいかが分かるようになります。

次の例題で余弦定理を使ってみましょう。

例題１

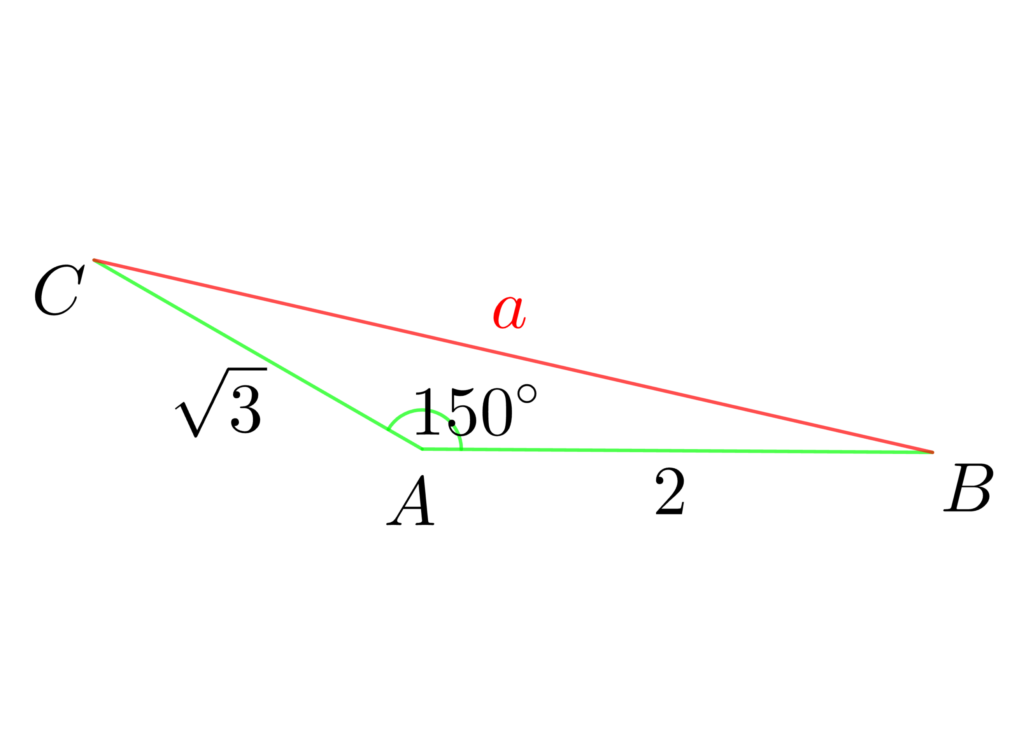
△ABCにおいて、\(b=\sqrt{3}\) 、\(c=2\)、\(A=150°\) のとき、\(a\) を求めよ。

まずは、図を書いてみます。

「２辺とその間の角から、対辺を求めるんだな」と認識できれば、あとは余弦定理を使いましょう。

\( \begin{aligned} \color{red}{a^2}&=\color{lime}{{(\sqrt{3}\:)}}^2+\color{lime}{{2\:}}^2-2\cdot\color{lime}{\sqrt{3}}\cdot \color{lime}{2}\cdot\color{lime}{\cos{150°}} \\ \\ &=3+4-2\cdot\sqrt{3}\cdot 2\cdot\left(-\frac{\sqrt{3}}{2}\right)\\ \\ &= 13\\ \end{aligned} \)

　
よって \(a>0\) より \(a=\sqrt{3}\)

余弦定理の使い方②

さん

次は、余弦定理を少し変形した式を使ってみよう！

余弦定理を「\(\cos =\)」の形に変形します。

\(\color{red}{a^2=b^2+c^2-2bc\cos{A}}\) より

\(2bc\cos{A}=b^2+c^2-a^2\)

よって \(\displaystyle\color{red}{\cos{A}=\frac{b^2+c^2-a^2}{2bc} }\)

この式は、「３辺から角が分かる式」です。

式変形のイメージがあれば、暗記しようと頑張らなくても頭の中で導出することができます。

次の例題でこの式を使ってみましょう。

例題２

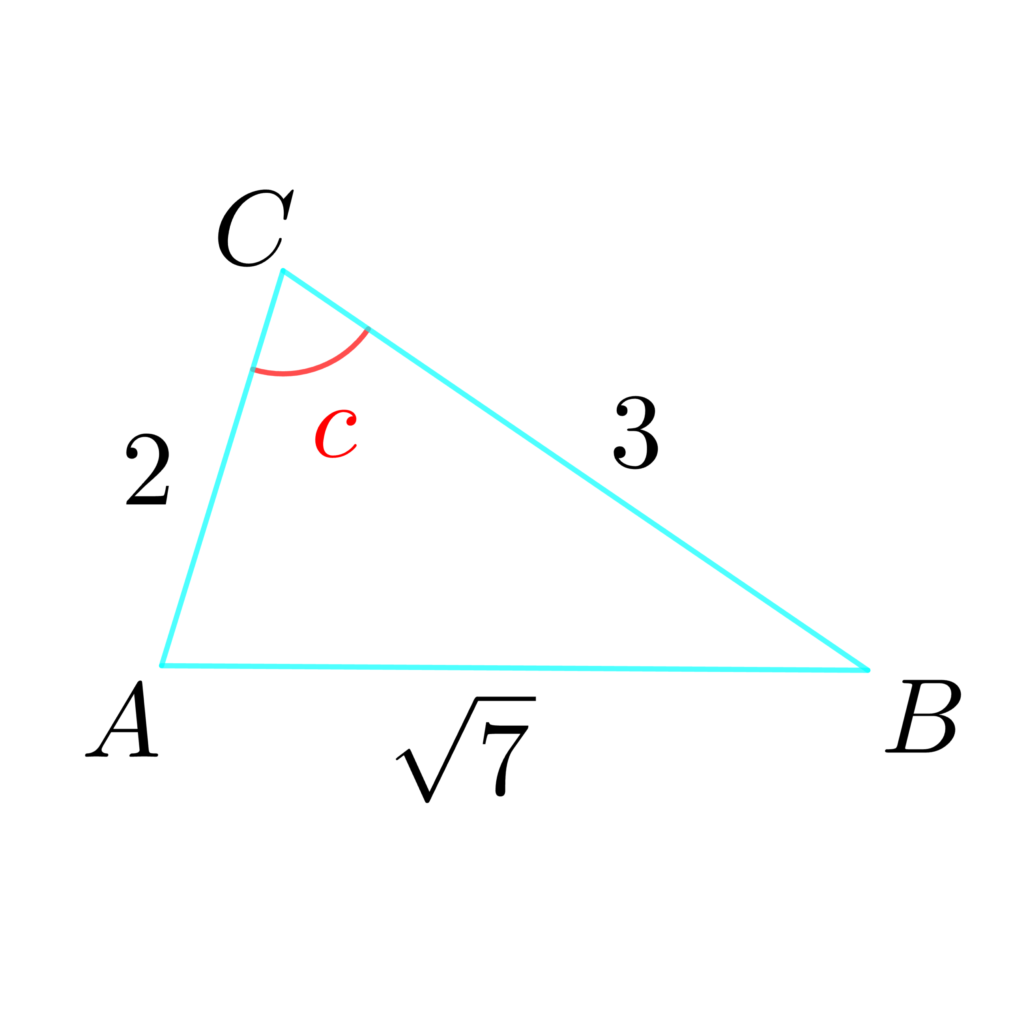
△ABCにおいて、\(b=\sqrt{6}\) 、\(A=45°\)、\(B=60°\) のとき、\(a\) を求めよ。

まずは、図を書いてみます。

「３辺から、角を求めるんだな」と認識できれば、あとは余弦定理を使いましょう。

\( \begin{aligned} \:\cos{C}&=\frac{\color{deepskyblue}{3}^2+\color{deepskyblue}{2}^2-(\color{deepskyblue}{\sqrt{7}})^2}{2\cdot \color{deepskyblue}{3}\cdot \color{deepskyblue}{2}} \\ \\ &=\frac{1}{2}\\ \end{aligned} \)

　
よって \(C = 60°\)

余弦定理が成り立つ理由

生徒

余弦定理はもともと三平方の定理ってどういうこと？

さん

余弦定理を導出してみよう！

次の三角形で余弦定理 \(a^2=b^2+c^2-2bc\cos{A}\) を導出していきます。

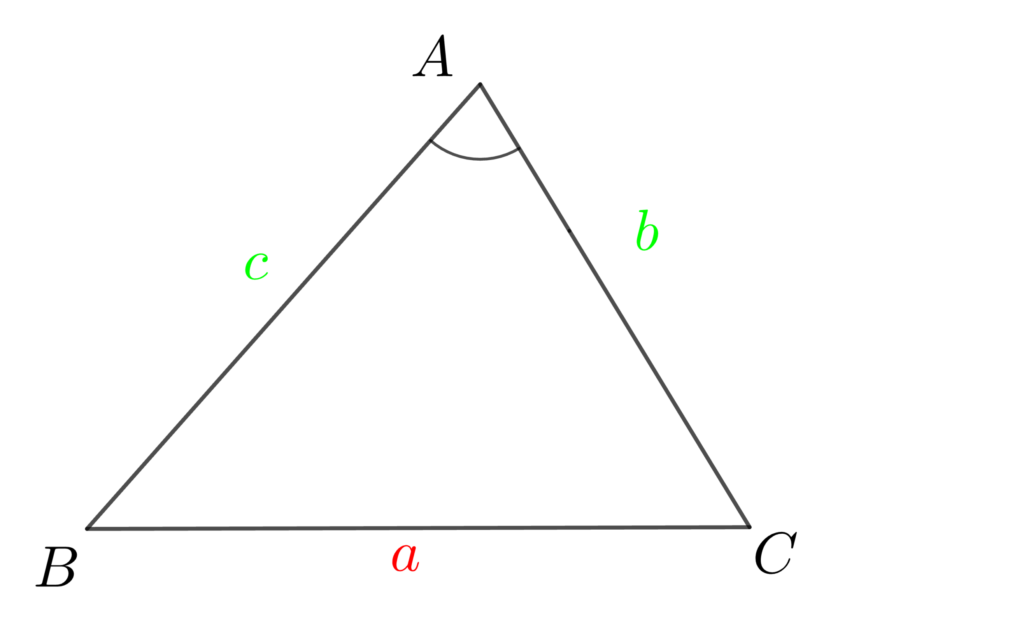
頂点BからACに垂線を引き、水色の直角三角形BCHで「三平方の定理」を使うと、それが「余弦定理」となります。

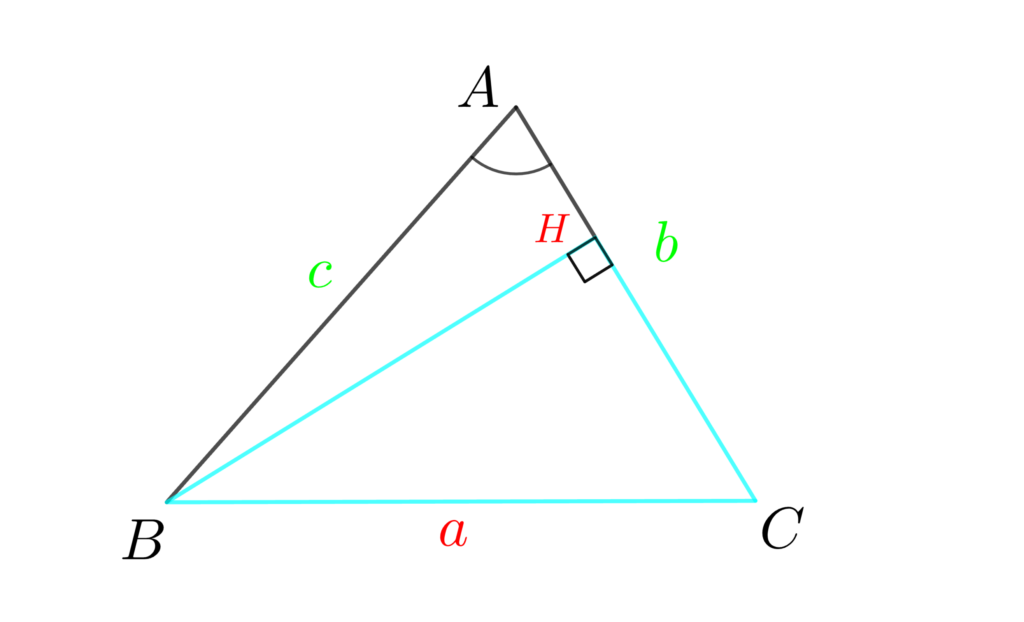
直角三角形BCHの１つの辺BCの長さは \(a\) と分かっていますので、残りの２辺BH、CHを求めていきます。

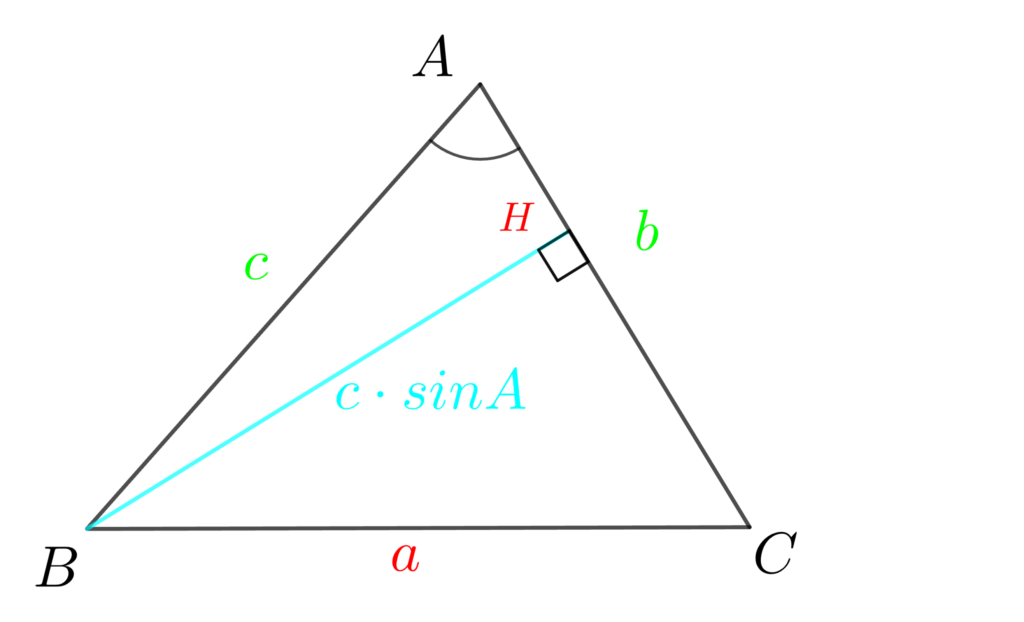
まずは、辺BHを考えます。直角三角形ABHより、\(BH=c\cdot\sin{A}\)

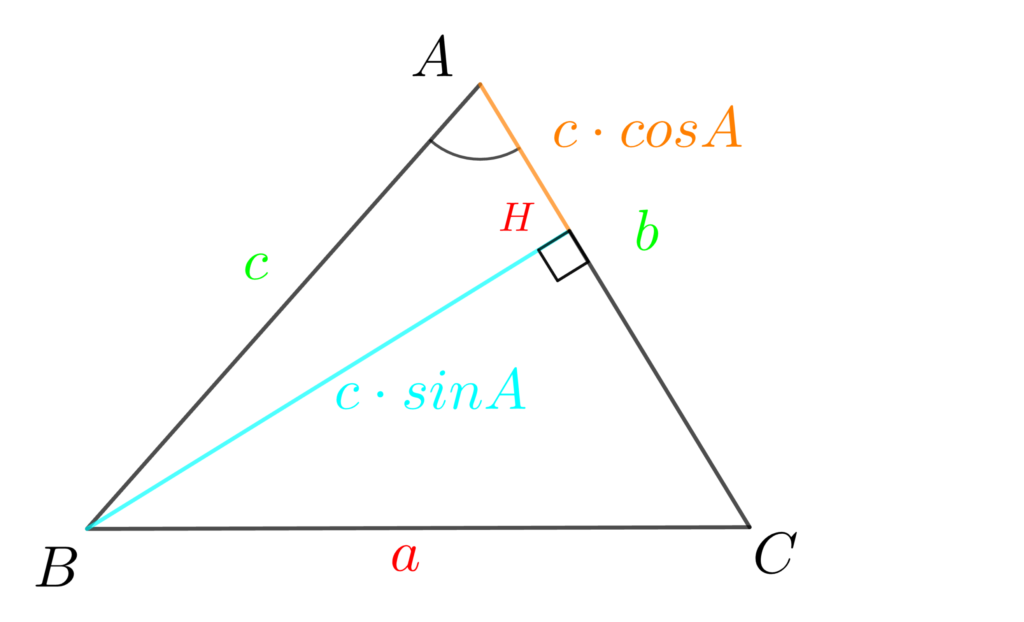
次に、辺CHを考えます。直角三角形ABHより、\(AH=c\cdot\cos{A}\) ですので、\(CH=b – c\cdot\cos{A}\)

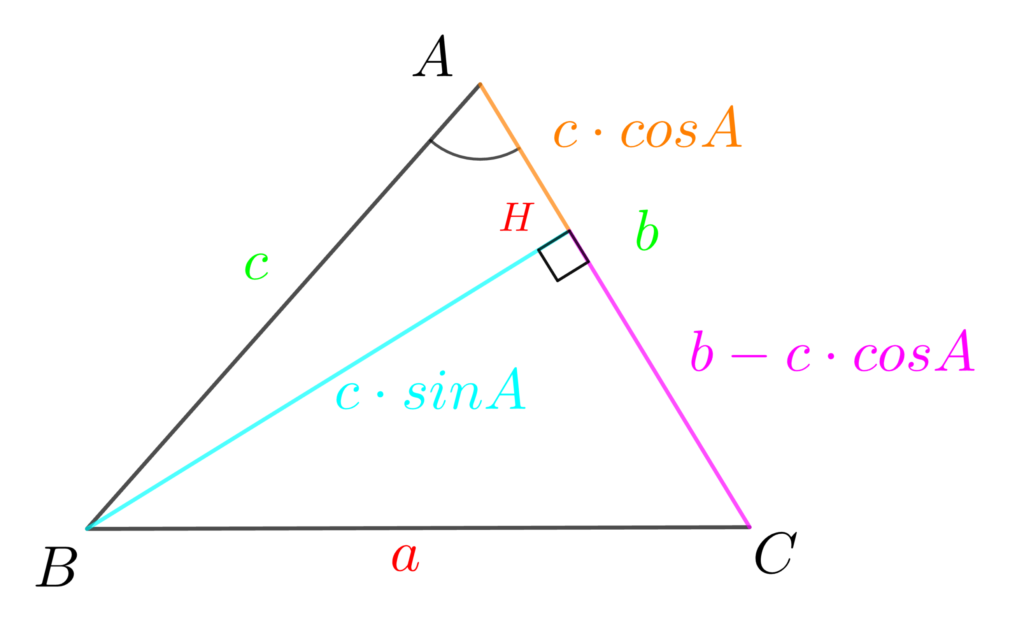
直角三角形BCHの３辺の長さが求まりましたので、あとは「三平方の定理」を使い「余弦定理」が導出します。

\( \begin{aligned} \displaystyle \color{red}{{BC}^2}&=\color{deepskyblue}{{BH}^2}+\color{hotpink}{{CH}^2} \\ \\ &=\color{deepskyblue}{({c\cdot\sin{A}})^2}+\color{hotpink}{{(b – c\cdot\cos{A}})^2} \\ \\ &= c^2{\sin{A}\:}^2+b^2-2bc\cos{A}+{c^2\cos{A}\:}^2 \\ \\ &= b^2+c^2({\sin{A}\:}^2+{\cos{A}\:}^2)-2bc\cos{A} \\ \\ &= \color{red}{b^2+c^2-2bc\cos{A}} \\ \end{aligned} \)

さん

相互関係式 \({\sin{A}\:}^2+{\cos{A}}^2=1\) を使ったよ！覚えてるかな？

【数学Ⅰ】三角比07：三角比の相互関係

三角比の「sin」「cos」「tan」はどうつながっているの？この記事では、三角比の相互関係式（3つの基本公式）を図と会話でわかりやすく解説します。例題付きで、sinの値からcosとtanを求める方法も丁寧に紹介！

まとめ：余弦定理

さん

さて、今回のまとめだよ！

余弦定理は「隣り合う２辺とその間の角から対辺が分かる式」であり、「３辺から角が分かる式」です。

余弦定理

\(a^2=b^2+c^2-2bc\cos{A}\)

\(b^2=c^2+a^2-2ca\cos{B}\)

\(c^2=a^2+b^2-2ab\cos{C}\)

例題

(1) △ABCにおいて、\(b=\sqrt{3}\) 、\(c=2\)、\(A=150°\) のとき、\(a\) を求めよ。

解答

(1) 余弦定理より

よって \(a>0\) より \(a=\sqrt{3}\)

(2) △ABCにおいて、\(b=\sqrt{6}\) 、\(A=45°\)、\(B=60°\) のとき、\(a\) を求めよ。

解答

(2) 余弦定理より

\(\displaystyle \cos{C}=\frac{\color{deepskyblue}{3}^2+\color{deepskyblue}{2}^2-(\color{deepskyblue}{\sqrt{7}})^2}{2\cdot \color{deepskyblue}{3}\cdot \color{deepskyblue}{2}}=\frac{1}{2}\)

よって

\(C = 60°\)