微分法の応用14：「不等式の証明」

「人より勉強に時間がかかる」と感じていませんか？

私のクラスにも、同じ悩みを抱えて苦しんでいた生徒がたくさんいました。

教科書の内容を理解するには、「自分で噛み砕いて考える力」が必要です。

このブログでは、よく寄せられる質問、つまずきやすいポイントをもとに、教科書の内容をわかりやすく解説していきます。

「噛み砕き方」がわかれば、文章はぐっと読みやすくなります！

まずは、教科書の説明を見てみましょう。

まずは教科書の説明

\(f(x)=e^x-(1+x)\) とすると \(f'(x)=e^x-1\)

\(x>0\) のとき、\(e^x>1\) より \(f'(x)>0\)

であるから、\(f(x)\) は \(x>0\) で増加する。

よって、\(x=0\) のとき \(f(x)>f(0)=0\)

したがって、\(x>0\) のとき\(e^x>1+x\)

簡単に説明するよ

不等式「\(f(x) > g(x)\)」を関数の増減を用いて証明する方法は

です。

詳しく説明するよ

不等式を、「関数の増減」を用いて証明する方法について説明していきます。

「A から B を引いても \(0\) より大きかった」ら「A が B より大きい」って言えるよねってことです。

そして、「0 より大きい」ことを証明する方法としては、

「\((　)^2≧0\) を利用する方法」や「相加平均と相乗平均の関係の利用する方法」などがありました。

今回は、「関数の増減を利用する方法」を説明していきます。

不等式「 \(e^x>1+x\) 」の証明の目標は、「 \(e^x-(1+x)\)\(>\)\(0\) 」を示すことでした。

そこで、左辺と右辺をそれぞれ関数として図的に考えていきます。

左辺を \(y=e^x-(1+x)\)

右辺を \(y=0\) （\(x\)軸）

と考えます。

そして、

にあると言うことで、「 \(e^x-(1+x)>0\) 」を示していきます。

上の増減表を完成させるために、「\(x>0\) のときの\(f'(x)\) の符号」 と 「\(f(0)\) の値」を考えていきます。

これで増減表の完成です。

増減表から、\(x>0\) の範囲での最小値が \(0\) より大きいことが読み取れます。

これで、 \(x>0\) の範囲で、「常に「左辺 \(y=e^x-(1+x)\)」が「右辺 \(y=0\) （\(x\)軸）」より上側」 であることが示せました。

ちなみに \(f(x)=e^x-(1+x)\) のグラフはこんな感じです。

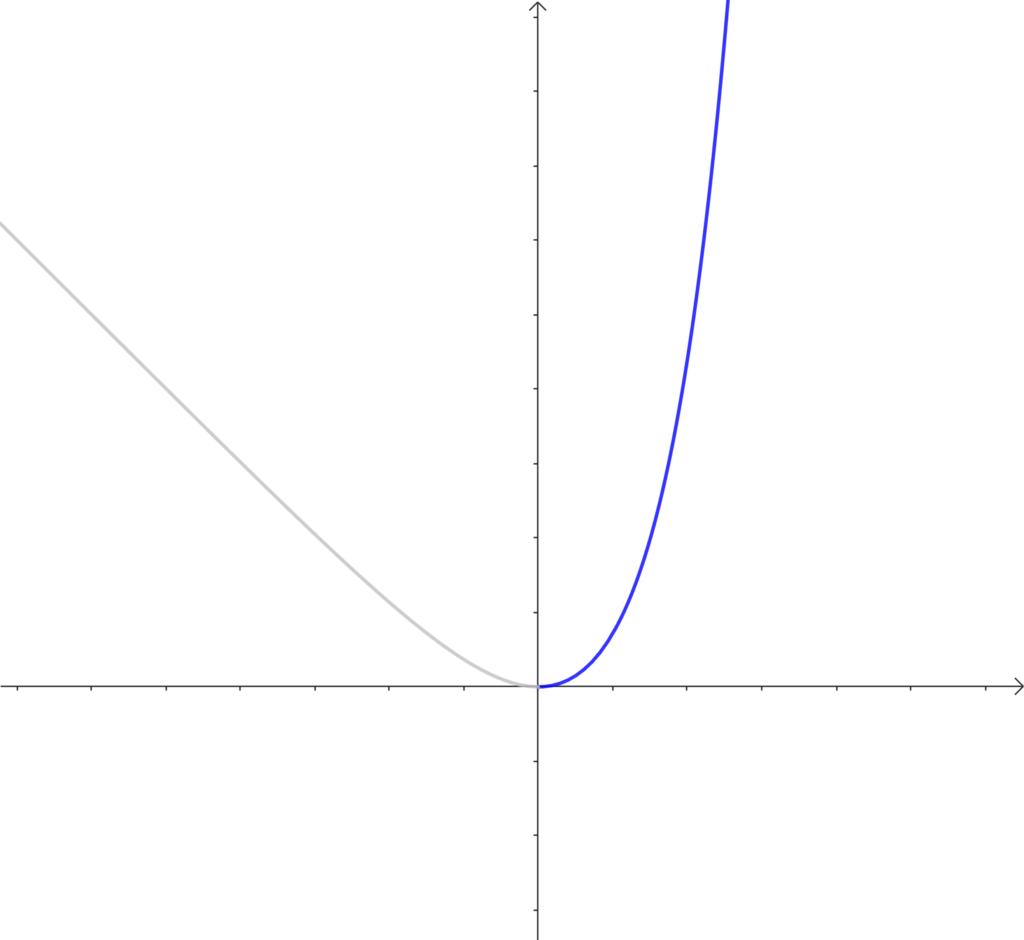
増減表さえ作成できれば、グラフを図示する必要はありません。

---

まとめ

今回の内容をしっかり整理しておこう！