
今日の板書はこれ!
正弦定理 \(\displaystyle\frac{a}{\sin{A}}=\frac{b}{\sin{B}}=\frac{c}{\sin{C}}\) は連比でも表せる
→ \(a:b:c=\sin{A}:\sin{B}:\sin{C}\)
☆ 比例式が与えられた場合、比率を文字で設定して通常の等式に変換する!
△ABC における次の等式が成り立つとき、この三角形の最大の角の大きさを求めよ。
\(\sin{A}:\sin{B}:\sin{C}=7:5:3\)
正弦定理より
よって、\(a=7k、b=5k、c=3k\) (\(k>0\)) とおける
また、最大辺は \(a\) であるから、最大角はAである
余弦定理より
よって、\(A=120°\)

もっと詳しく願いします!!
現役教員として数学を教えている「さん」と申します。
「人より勉強に時間がかかる」と感じていませんか?
私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。
• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」
• 「解答の意味が理解できず、勉強が進まない」
教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。
でも大丈夫!
このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。
意味から理解し、噛み砕き方をマスターしましょう!!
正弦定理 a:b:c=sinA:sinB:sinC を理解しよう!

正弦定理って \(\displaystyle\frac{a}{\sin{A}}=\frac{b}{\sin{B}}=\frac{c}{\sin{C}}=2R\) じゃないの?

その通り!今回は正弦定理の形を「比の形」に変形させ、使ってみよう!
正弦定理 \(\displaystyle\frac{a}{\sin{A}}=\frac{b}{\sin{B}}=\frac{c}{\sin{C}}\) は連比でも表せる
→ \(a:b:c=\sin{A}:\sin{B}:\sin{C}\)
分数と比の関係

まずは、分数と比の関係について復習していこう!
比例式は掛け算で表すことができました。
\(\color{hotpink}{a}:\color{deepskyblue}{b}=\color{deepskyblue}{c}:\color{hotpink}{d}\iff\color{hotpink}{a\times d}=\color{deepskyblue}{b\times c}\)
この式の両辺を \(\color{lime}{c\times d}\) で割ると
\(\displaystyle\frac{\color{hotpink}{a\times d}}{\color{lime}{c\times d}}=\frac{\color{deepskyblue}{b\times c}}{\color{lime}{c\times d}} \iff \color{red}{\frac{a}{c}=\frac{b}{d}}\)
よって、
\(\displaystyle a:b=c:d\iff\frac{a}{c}=\frac{b}{d}\)
このように、比例式は分数でも表すことができます。
そして逆に、分数の式は比例式で表すことができるとも言えます。
\(\displaystyle\color{red}{\frac{a}{c}=\frac{b}{d}\iff a:b=c:d}\)

\(\displaystyle \frac{1}{3}=\frac{2}{6}\iff1:2=3:6\) ってことか!

そうだね!分数で表せれた式も比例式って覚えておこう!
さらに、文字が増えてもこの関係は成り立ちます。
\(\displaystyle\color{red}{\frac{a}{d}=\frac{b}{e}=\frac{c}{f}}\)
\(\displaystyle\color{red}{\iff a:b:c=d:e:f}\)
正弦定理を比で表す
正弦定理は次の分数の形で表されていました。
\(\displaystyle\frac{a}{\sin{A}}=\frac{b}{\sin{B}}=\frac{c}{\sin{C}}\)
この分数の式も比例式で表すことができます。
\(\displaystyle\frac{a}{\sin{A}}=\frac{b}{\sin{B}}=\frac{c}{\sin{C}}\)
\(\iff a:b:c=\sin{A}:\sin{B}:\sin{C}\)

おー!正弦定理は比例式でも表すことができるんだね!

分数の式は比例式!
比の形の正弦定理を例題で使ってみよう!

次の問題で、実際に使ってみよう!
△ABC における次の等式が成り立つとき、この三角形の最大の角の大きさを求めよ。
\(\sin{A}:\sin{B}:\sin{C}=7:5:3\)
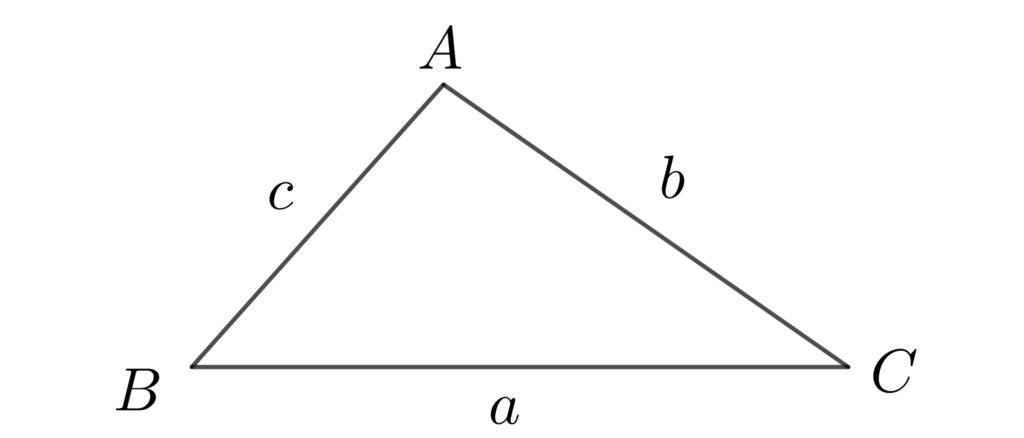
この問題は、sinの比から、角度を求める問題です。
\(\sin{A}:\sin{B}:\sin{C}=7:5:3\) は、比の形の正弦定理と全く同じですので、次のことが成り立ちます。
正弦定理 \(a:b:c=\sin{A}:\sin{B}:\sin{C}\) より、\(a:b:c=7:5:3\)
sinの比から、辺の長さの比を求めることができました。

sinの比は辺の長さの比ってことか!
正弦定理の役目はここまでです。
正弦定理とは別に、数学の定石として覚えてもらいたいことがあります。
それは、「比例式が与えられた場合は、文字で設定する」です。
\(a:b:c=7:5:3\) より、定数 \(k\) \((k>0)\) を用いて
\(a=7k\)、\(b=5k\)、\(a=3k\) とおく。
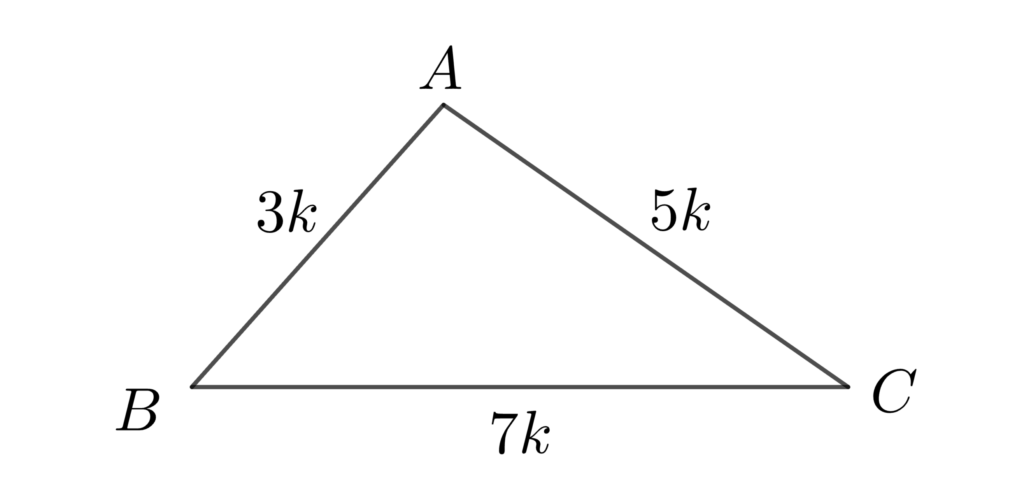

この作業を行うと、ただの比だったものを、実際の長さとして扱えるようになるんだ!
三角形の3辺の長さがわかったので、角度を求めていきます。

3辺の長さから角度を求めるには、どうすればよかったっけ?

あっ!余弦定理!!ところで最大角ってどこ?
この問題では、「最大角の大きさを求めよ」と言われていますので、どの角が一番大きいのかを判断しないといけません。
「三角形の角の大小は、辺の大小と一致する」
図を見れば、当たり前のことだと理解できると思いますが、覚えておきましょう。
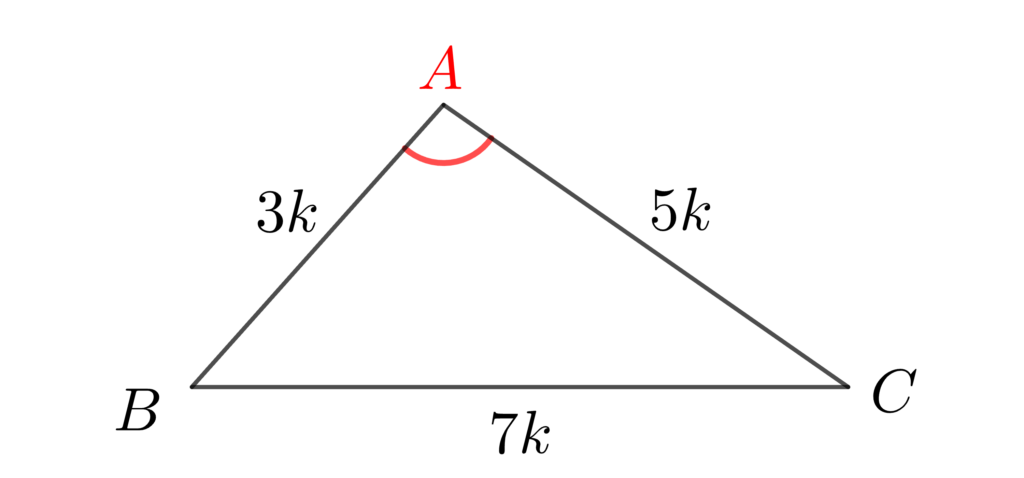
一番長い辺は \(a\) なので、一番大きい角は \(A\) です。
あとは、余弦定理で角度を求めればおしまいです。
余弦定理より
よって、\(A=120°\)
まとめ:正弦定理の比例式

さて、今回のまとめだよ!
正弦定理 \(\displaystyle\frac{a}{\sin{A}}=\frac{b}{\sin{B}}=\frac{c}{\sin{C}}\) は連比でも表せる
→ \(a:b:c=\sin{A}:\sin{B}:\sin{C}\)
☆ 比例式が与えられた場合、比率を文字で設定して通常の等式に変換する!
△ABC における次の等式が成り立つとき、この三角形の最大の角の大きさを求めよ。
\(\sin{A}:\sin{B}:\sin{C}=7:5:3\)
正弦定理より
よって、\(a=7k、b=5k、c=3k\) (\(k>0\)) とおける
また、最大辺は \(a\) であるから、最大角はAである
余弦定理より
よって、\(A=120°\)

また一つ賢くなった!





コメント