
今日の板書はこれ!
\(S=\displaystyle \frac{1}{2}r(a+b+c)\)
- 他の方法で面積Sを求める
- \(S=\displaystyle \frac{1}{2}r(a+b+c)\) を用いる
△ABCにおいて、\(a=5\), \(b=6\), \(c=7\) のとき、この三角形の内接円の半径 \(r\) を求めよ。
余弦定理より \(\displaystyle \color{red}{\cos{A}=\frac{{7}^2+{6}^2-{5}^2}{2 \cdot 7 \cdot 6}} = \frac{5}{7}\)
\(\sin{A}>0\) より \(\displaystyle \color{red}{\sin{A}=\sqrt{1-\left(\frac{5}{7}\right)^2}}=\frac{2\sqrt{6}}{7}\)
△ABCの面積をSとすると \(\displaystyle \color{red}{S=\frac{1}{2} \cdot 6 \cdot 7 \cdot \frac{2\sqrt{6}}{7}} =6\sqrt{6}\)
△ABC\(\displaystyle =\frac{1}{2}r(a+b+c)\)より \(\displaystyle 6\sqrt{6}=\frac{1}{2}r(5+6+7)\)
よって \(\displaystyle r=\frac{2\sqrt{6}}{3}\)

もっと詳しく願いします!!
現役教員として数学を教えている「さん」と申します。
「人より勉強に時間がかかる」と感じていませんか?
私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。
• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」
• 「解答の意味が理解できず、勉強が進まない」
教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。
でも大丈夫!
このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。
意味から理解し、噛み砕き方をマスターしましょう!!
三角形の面積公式と内接円の半径の求め方
三角形の内接円の半径を使った面積公式

まずは、三角形の面積を「内接円の半径を使って求める方法」を紹介するね!
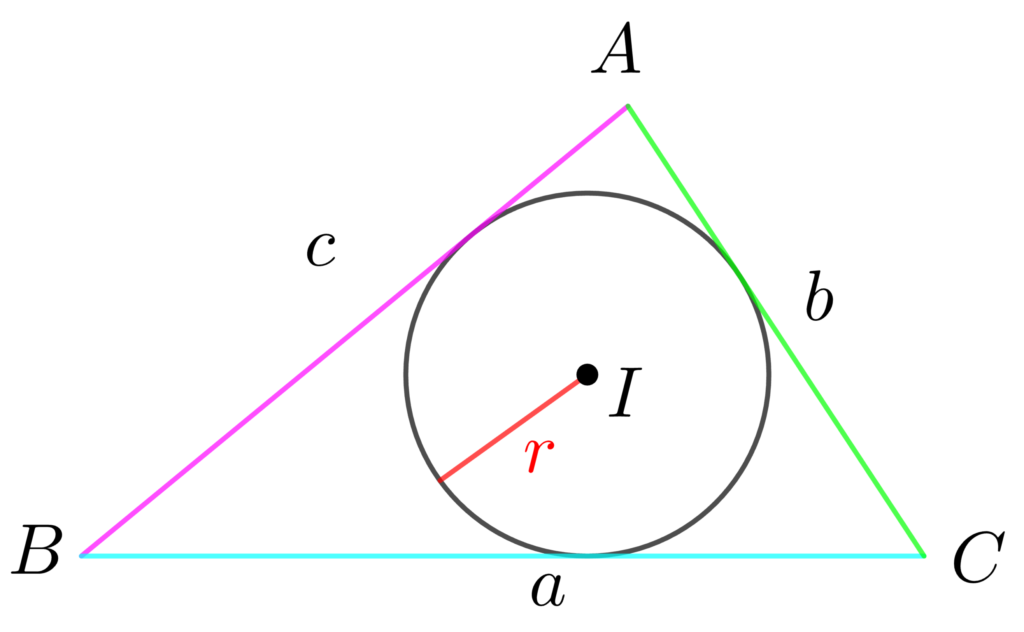
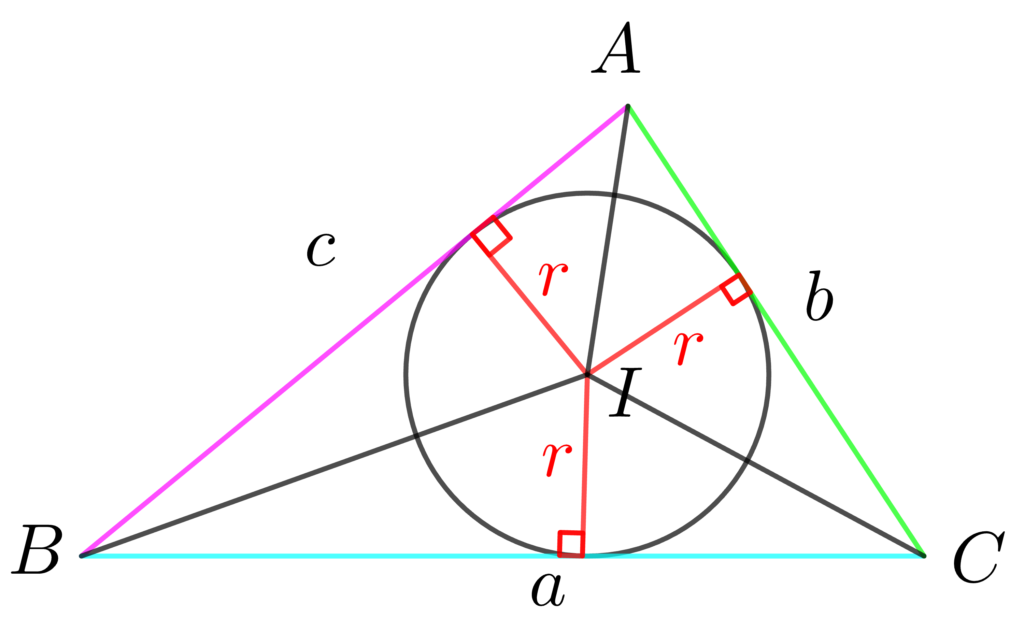
まずは、△ABCを \(\color{deepskyblue}{△BCI}\) と \(\color{lime}{△CAI}\) と \(\color{hotpink}{△ABI}\) の3つの三角形に分けます。
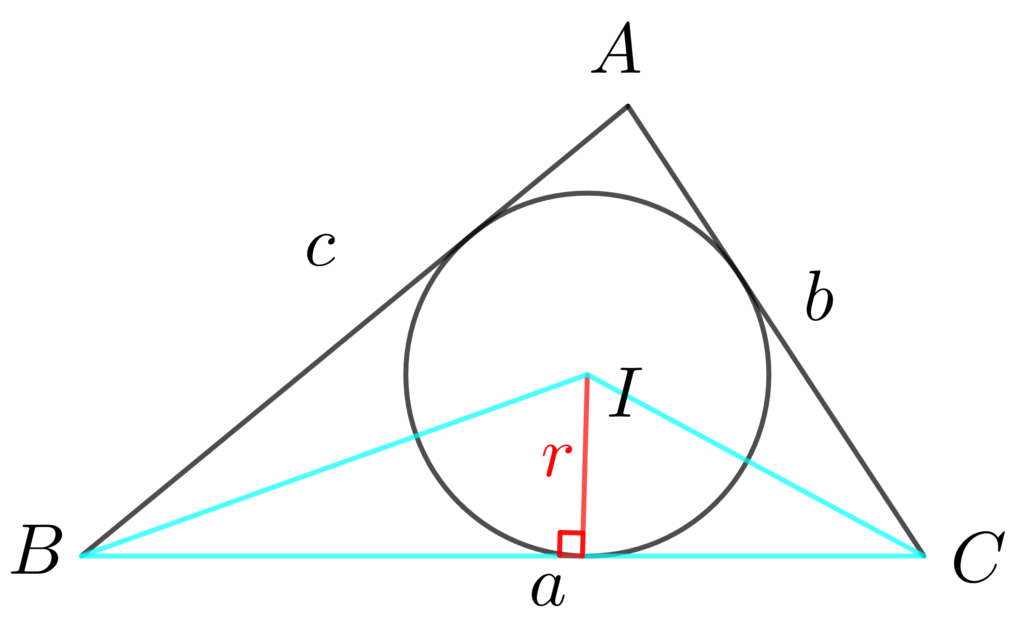
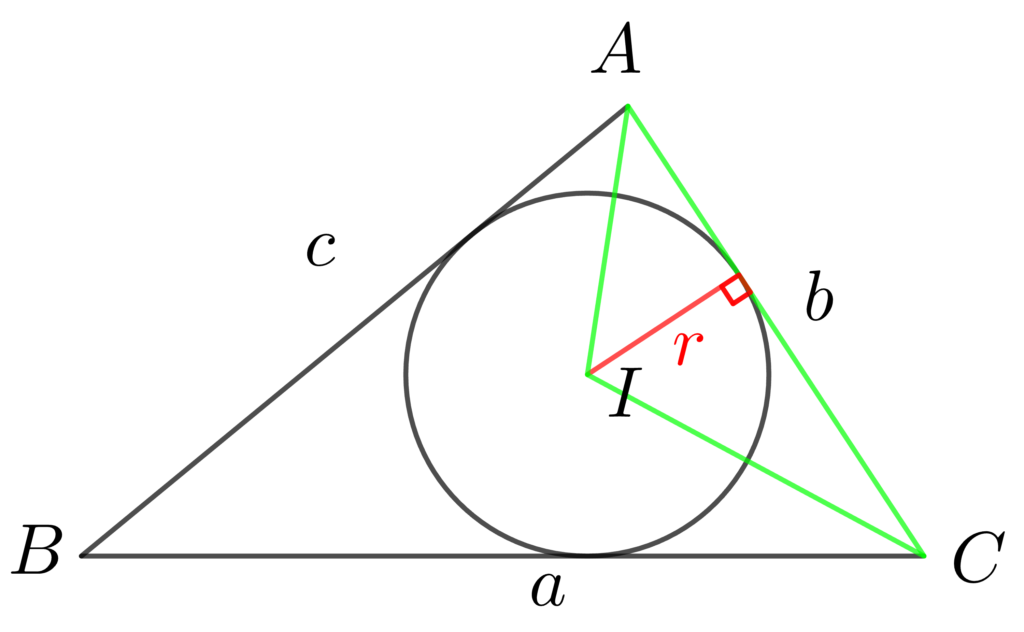
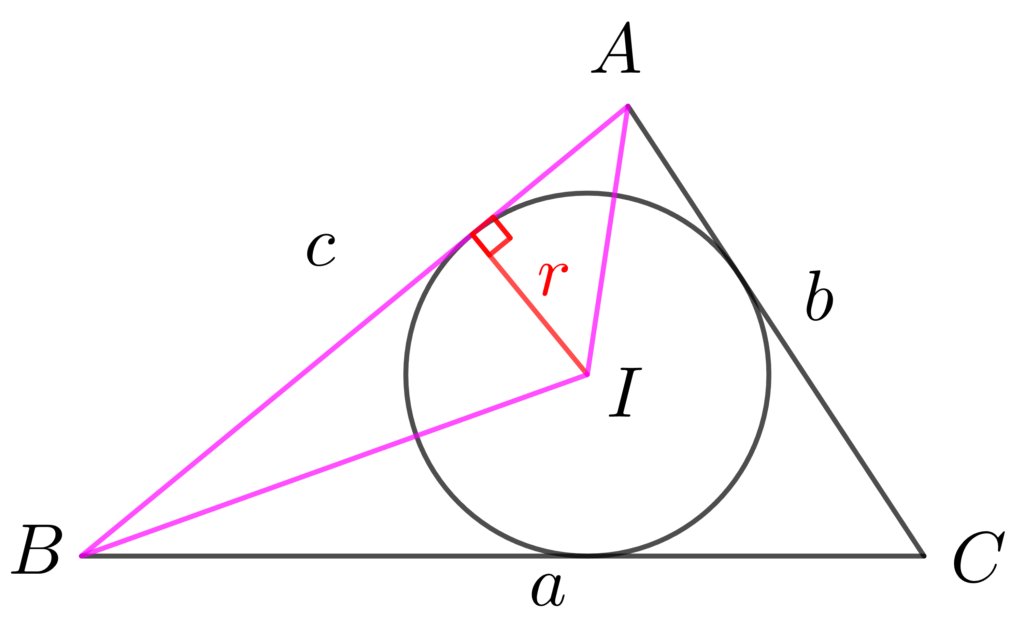
そして、それぞれの三角形の面積を足し合わせると△ABCの面積を求めることができます。
\(\displaystyle\color{deepskyblue}{△BCI}=\frac{1}{2}\cdot \color{deepskyblue}{a} \cdot \color{red}{r}\) 、 \(\displaystyle\color{lime}{△CAI}=\frac{1}{2}\cdot \color{lime}{b} \cdot \color{red}{r}\) 、 \(\displaystyle\color{hotpink}{△ABI}=\frac{1}{2}\cdot \color{hotpink}{c} \cdot \color{red}{r}\)
よって

この結果は公式として覚えておいた方がいいやつだね!
\(\displaystyle S=\frac{1}{2}r(a+b+c)\)
内接円の半径の求め方

次の例題で内接円の半径を求めよう!
△ABCにおいて、\(a=5\), \(b=6\), \(c=7\) のとき、この三角形の内接円の半径 \(r\) を求めよ。
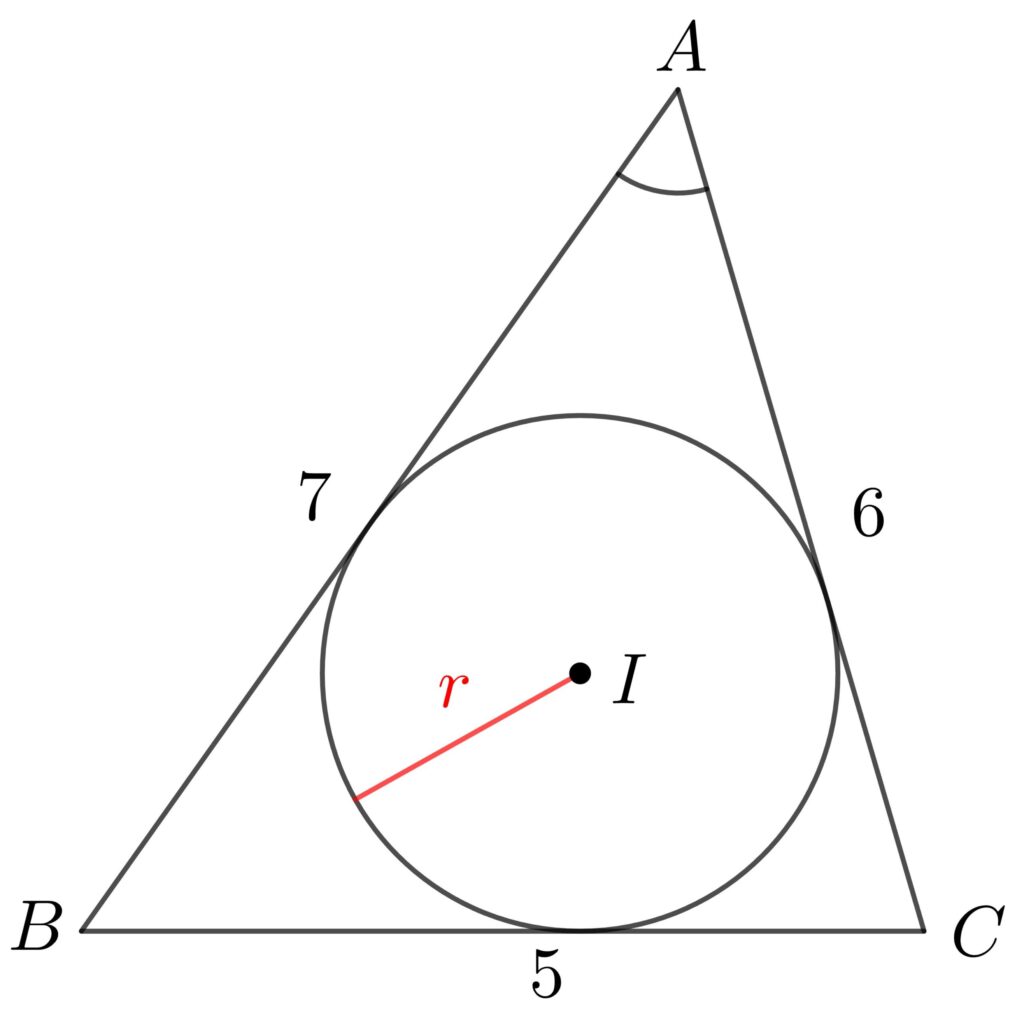
内接円の半径は、次の手順で求めます。
- 他の方法で面積Sを求める。
- \(\displaystyle S=\frac{1}{2}r(a+b+c)\) を用いる。
他の方法で面積Sを求める。
三角比による三角形の面積公式 \(S=\frac{1}{2}bc\sin{A}\) を使って面積を求めていきます。
余弦定理より \(\displaystyle \color{red}{\cos{A}=\frac{{7}^2+{6}^2-{5}^2}{2 \cdot 7 \cdot 6}} = \frac{5}{7}\)
\(\sin{A}>0\) より \(\displaystyle \color{red}{\sin{A}=\sqrt{1-\left(\frac{5}{7}\right)^2}}=\frac{2\sqrt{6}}{7}\)
△ABCの面積をSとすると \(\displaystyle \color{red}{S=\frac{1}{2} \cdot 6 \cdot 7 \cdot \frac{2\sqrt{6}}{7}} =6\sqrt{6}\)
\(\displaystyle S=\frac{1}{2}r(a+b+c)\) を用いる。
面積 \(S=6\sqrt{6}\) ですので、方程式を立てます。
△ABC\(\displaystyle =\frac{1}{2}r(a+b+c)\)より \(\displaystyle 6\sqrt{6}=\frac{1}{2}r(5+6+7)\)
よって \(\displaystyle r=\frac{2\sqrt{6}}{3}\)

内接円の半径を求めるには、面積を考えるんだね!
まとめ:三角比による三角形の面積

さて、今回のまとめだよ!
\(S=\displaystyle \frac{1}{2}r(a+b+c)\)
- 他の方法で面積Sを求める
- \(S=\displaystyle \frac{1}{2}r(a+b+c)\) を用いる
△ABCにおいて、\(a=5\), \(b=6\), \(c=7\) のとき、この三角形の内接円の半径 \(r\) を求めよ。
余弦定理より \(\displaystyle \color{red}{\cos{A}=\frac{{7}^2+{6}^2-{5}^2}{2 \cdot 7 \cdot 6}} = \frac{5}{7}\)
\(\sin{A}>0\) より \(\displaystyle \color{red}{\sin{A}=\sqrt{1-\left(\frac{5}{7}\right)^2}}=\frac{2\sqrt{6}}{7}\)
△ABCの面積をSとすると \(\displaystyle \color{red}{S=\frac{1}{2} \cdot 6 \cdot 7 \cdot \frac{2\sqrt{6}}{7}} =6\sqrt{6}\)
△ABC\(\displaystyle =\frac{1}{2}r(a+b+c)\)より \(\displaystyle 6\sqrt{6}=\frac{1}{2}r(5+6+7)\)
よって \(\displaystyle r=\frac{2\sqrt{6}}{3}\)

また一つ賢くなった!






コメント