【数学A】場合の数02：場合の数の数え方

---

---

現役教員として数学を教えている「さん」と申します。

「人より勉強に時間がかかる」と感じていませんか？

私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。

教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。

でも大丈夫！

このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。

意味から理解し、噛み砕き方をマスターしましょう！！

場合の数の数え方

次の例題を考えてみましょう。

数え方の１つ目のポイントは「起こりうる全ての場合の数を漏れなく・重複なく数え上げること」です。

複雑な問題になればなるほど、数え忘れていたり、同じものを２度数えていたりしてしまいます。

大切なポイントですのでもう一度、「漏れなく・重複なく」数えましょう。

「漏れなく・重複なく」考えるために表や樹形図を活用します。

---

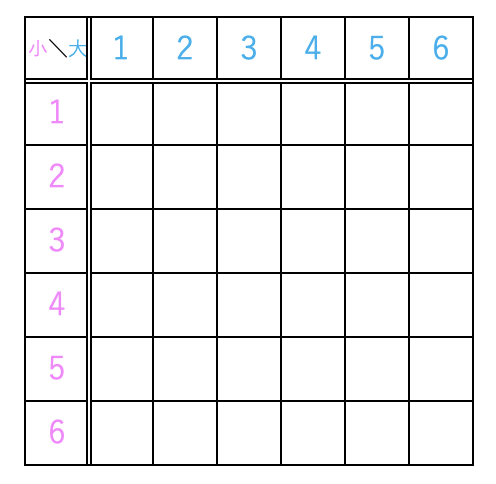
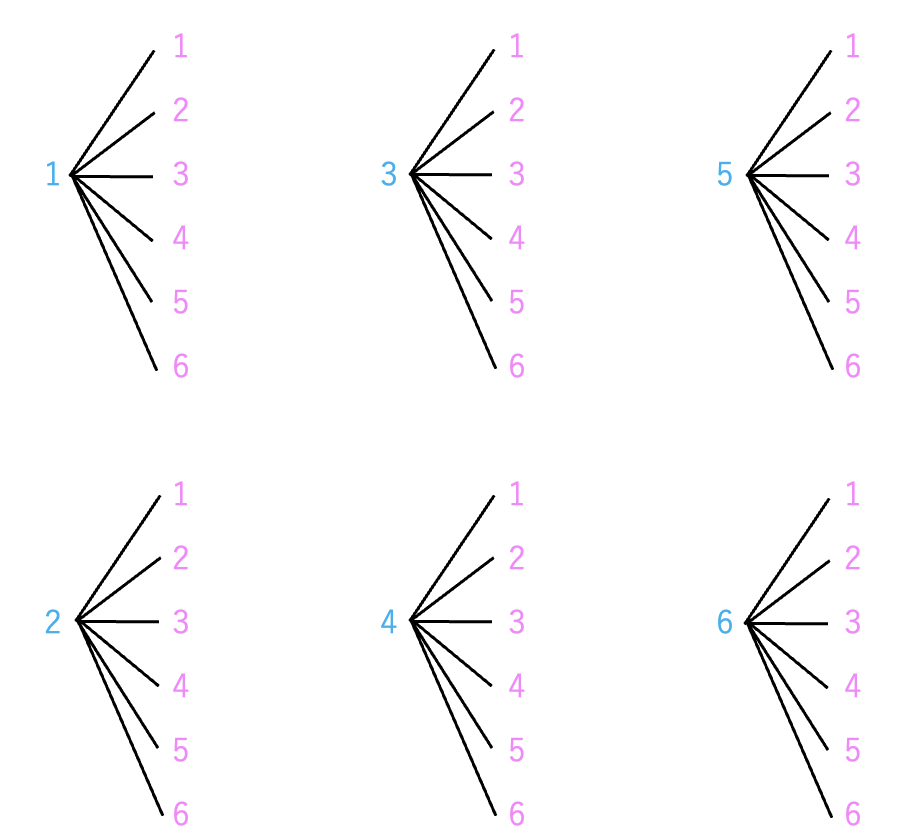
まずは、(1) 目の和が5の倍数になる場合が何通りあるのかを数えていきます。

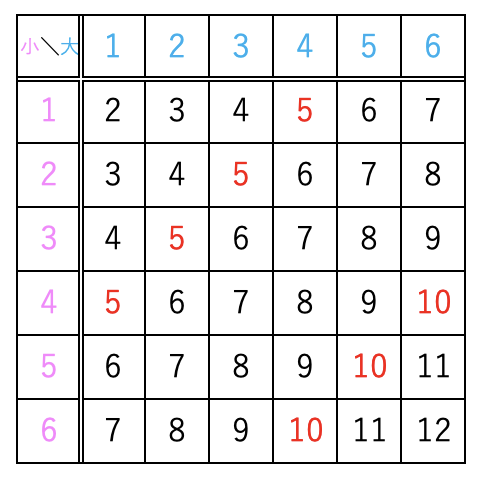
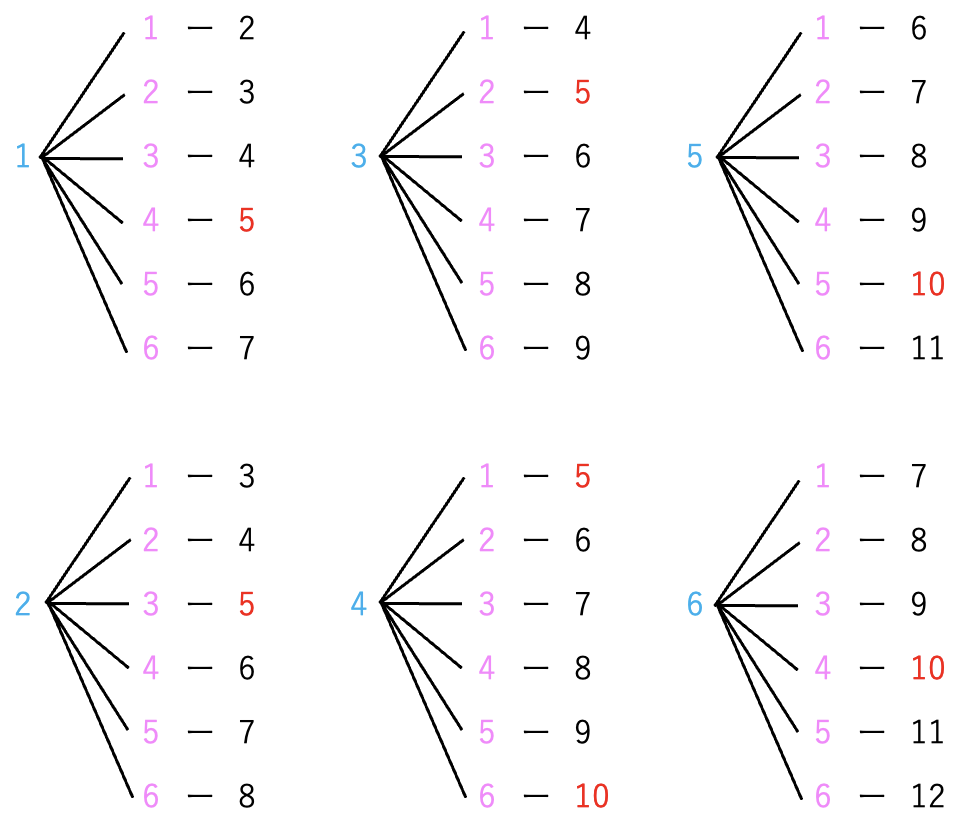
表や樹形図から、合計で７通りあることがわかりました。

---

次に、(2) 大きいサイコロの目が3以上で、小さいサイコロの目が偶数になる場合の数が何通りあるかを数えていきます。

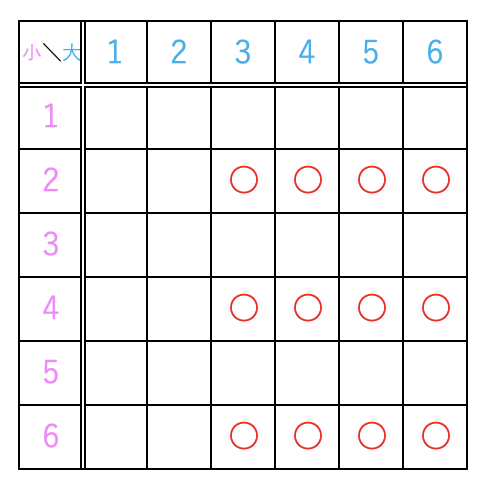
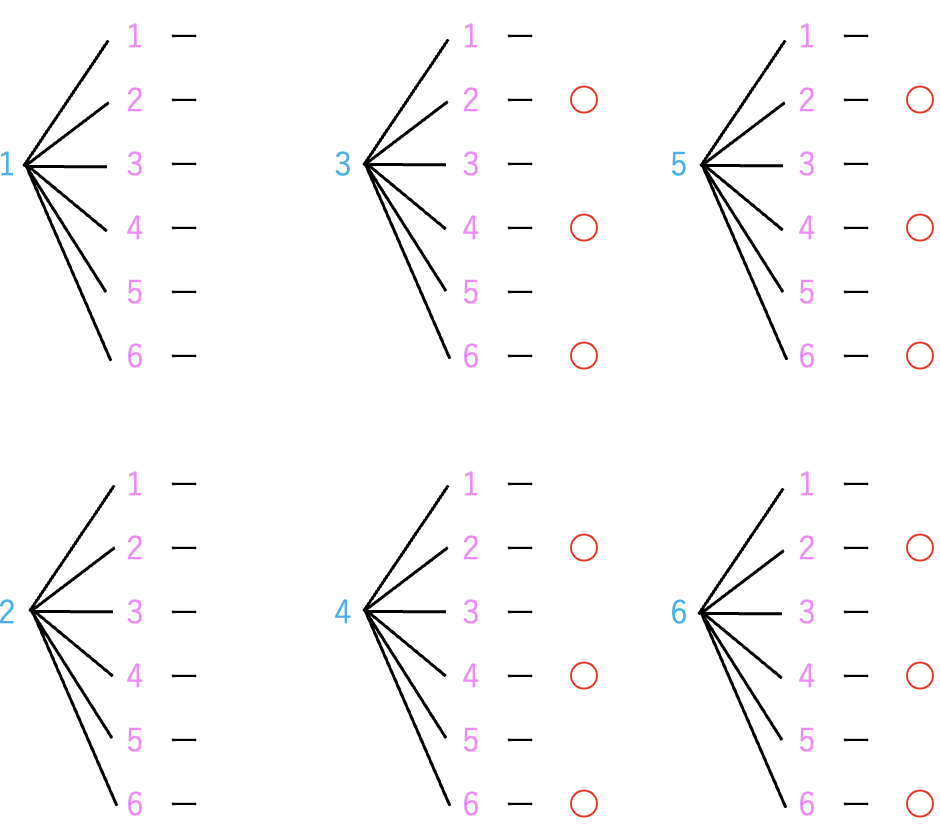
表や図形ずから、合計で12通りあることがわかりました。

---

中学までの数学では、この数え方でOKでした。

しかし、高校数学で1000通り以上の場合の数を数える問題が普通に出てきます。

ここで、数え方の２つ目のポイントです。

「和の法則と積の法則を使い効率よく数えること」です。

和の法則

「目の和が５の倍数」という事象は、事象A「目の和が５」でもいいし、 事象B「目の和が１０」が起きてもOKです。

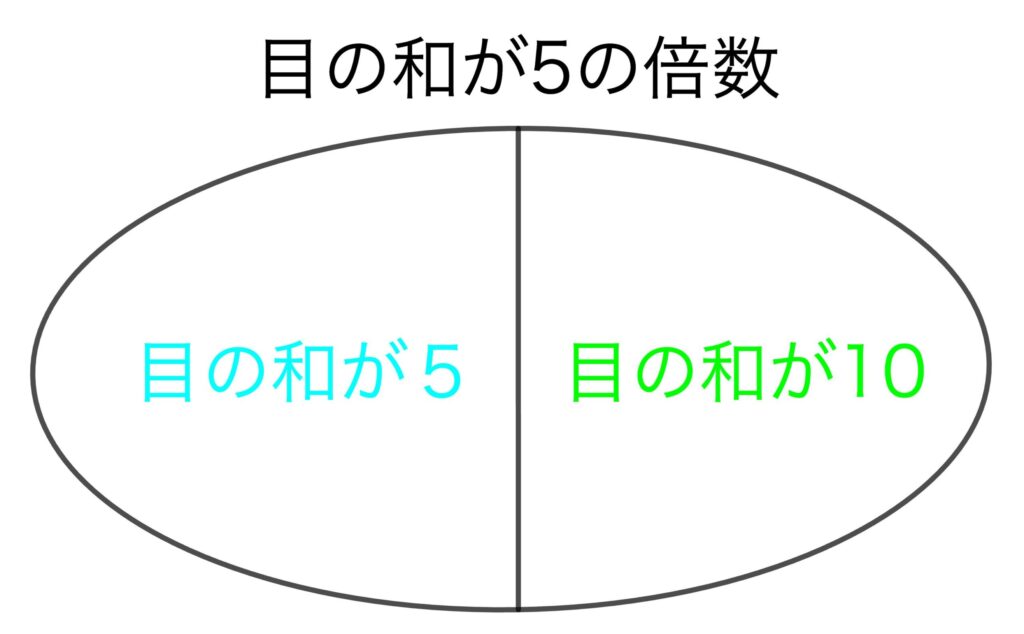
事象A「目の和が５」は (大, 小) = (1, 4), (2, 3), (3, 2), (4, 1) の4通り。

事象B「目の和が１０」は (大, 小) = (4, 6), (5, 5), (6, 4) の3通り。

よって、求めたい事象「目の和が５の倍数になる」のは \(4+3\) で 7通り と考えることができます。

「和の法則」とは、「求めたい事象がAでもいいしBでもいいなら、足してあげればいいよね」という考え方です。

積の法則

「大きいサイコロの目が3以上で、小さいサイコロの目が偶数になる」という事象は、\(\color{deepskyblue}{事象A「大きいサイコロの目が3以上」}\)であり、さらに \(\color{hotpink}{事象B「小さいサイコロの目が偶数」}\)でなくてはいけません。

事象A「大きいサイコロの目が3以上」は 3, 4, 5, 6 の4通り。

事象B「小さいサイコロの目が偶数」は 2, 4, 6 の3通り。

「大きいサイコロの目が3以上で、小さいサイコロの目が偶数になる」のは、事象Aの4通りそれぞれに対して、事象Bが3通り存在します。

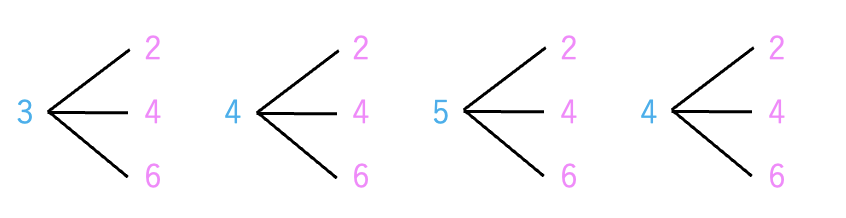
よって、求めたい事象は \(4×3\) で 12通り と考えることができます。

「積の法則」とは、「求めたい事象がAが起き、それぞれに対してBが起きるなら、掛けてあげればいいよね」という考え方です。

和の法則と積の法則の使い分け

和の法則と積の法則をもう一度確認してみましょう。

アイスが３種類、ケーキが２種類あるとします。

「アイスを食べてもいいし、ケーキを食べてもいい」ときは足す。（\(3+2=5\)通り）

「アイスを食べて、さらにケーキを食べる」ときは掛ける。（\(3×2=6\)通り）

こんなイメージです。

アイスを食べるかケーキを食べるなら数を足し、アイスを食べてジュースも飲むなら掛ける。

「どちらでもいいときが和の法則」か、「両方必要な時が積の法則」です。

まとめ：三角比による三角形の面積

---

---