【なぜ？が解決！】約数の個数と総和の求め方を徹底解説！

さん

今日の板書はこれ！

約数の個数

ある自然数が\(\color{deepskyblue}{〇^a}×\color{hotpink}{△^b}×\color{lime}{◻︎^c}\)と素因数分解できるとき、その約数の個数は

\(\color{deepskyblue}{(a+1)}×\color{hotpink}{(b+1)}×\color{lime}{(c+1)}\)

約数の総和

ある自然数が\(\color{deepskyblue}{〇^a}×\color{hotpink}{△^b}×\color{lime}{◻︎^c}\)と素因数分解できるとき、その約数の総和は

\( \begin{aligned} \color{deepskyblue}{(〇^0+〇^1+\cdots+〇^a)}\color{hotpink}{(△^0+△^1+\cdots+△^b)}\color{lime}{(◻︎^0+◻︎^1+\cdots+◻︎^c)} \end{aligned} \)

生徒

もっと詳しく願いします！！

現役教員として数学を教えている「さん」と申します。

「人より勉強に時間がかかる」と感じていませんか？

私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。

• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」

• 「解答の意味が理解できず、勉強が進まない」

教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。

でも大丈夫！

このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。

意味から理解し、噛み砕き方をマスターしましょう！！

勉強しても成績が上がらない3つの理由と現役教師が教えるたった1つの解決策

一生懸命やってるのに結果が出ない…そんな中高生の悩みを、現役教師が本気で解決！信頼できる家庭教師が導く正しい学び方とは？

約数の個数と総和
1. 約数の個数
2. 約数の総和
まとめ：約数の個数と総和

約数の個数と総和

さん

12の「約数の個数」と「約数の総和」について考えていこう！

\(12\)の約数は「素因数の組み合わせ」でした。

\(12=\color{deepskyblue}{2^2}×\color{hotpink}{3^1}\) より \(24\)の約数は \(1, 2, 3, 4, 6, 12\)

生徒

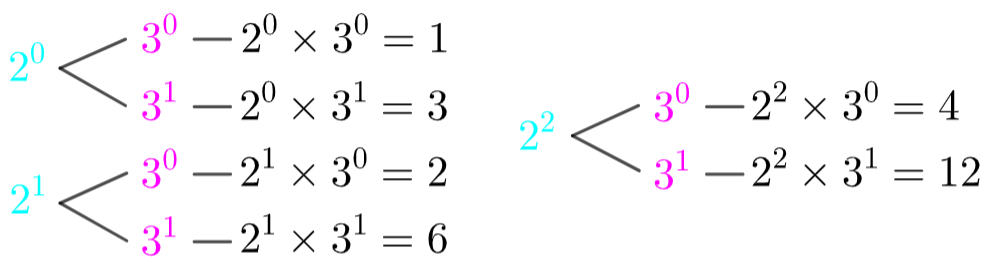
\(2^0\) や \(3^0\) みたいに、０乗は全部 \(1\) になるんだったね！

約数の個数

さん

約数の個数を効率よく考えていこう！

約数は「素因数の組み合わせ」ですので、\(12\)の約数の個数を「積の法則」を使って求めていきます。

\(12=\color{deepskyblue}{2^2}×\color{hotpink}{3^1}\) より、

\(\color{deepskyblue}{2}\) は \(\color{deepskyblue}{2^0}, \color{deepskyblue}{2^1}, \color{deepskyblue}{2^2}\) の \(3\) 通り。

\(\color{hotpink}{3}\) は \(\color{hotpink}{3^0}, \color{hotpink}{3^1}\) の \(2\) 通り。

よって、\(12\) の約数の個数は、\(3×2=6\) 通り。

生徒

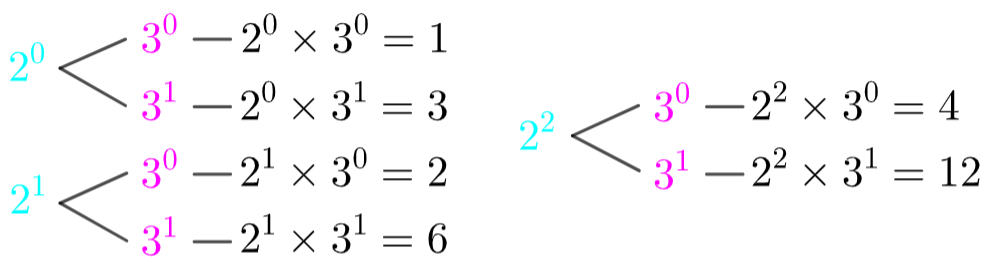
実際に約数を求めなくてもわかるの便利だね！！

「約数の個数」の公式は次の通りです。

約数の個数

ある自然数が\(\color{deepskyblue}{〇^a}×\color{hotpink}{△^b}×\color{lime}{◻︎^c}\)と素因数分解できるとき、その約数の個数は

\(\color{deepskyblue}{(a+1)}×\color{hotpink}{(b+1)}×\color{lime}{(c+1)}\)

この公式を使って求めてみます。

\(12=\color{deepskyblue}{2^2}×\color{hotpink}{3^1}\) であるから、

\(12\) の約数の個数は\((\color{deepskyblue}{2}+1)(\color{hotpink}{1}+1)=6\)

生徒

公式の \(+1\) って、0乗の分ってことか！

約数の総和

さん

次は約数の総和を効率よく考えていこう！

\(24\) の約数は \(1, 2, 3, 4, 6, 12\) でした。

よって、総和は次のように求めれます。

\(1+2+3+4+6+12=28\)

これを、素因数分解の結果 \(12=2^2×3^1\) を使って求めてみます。

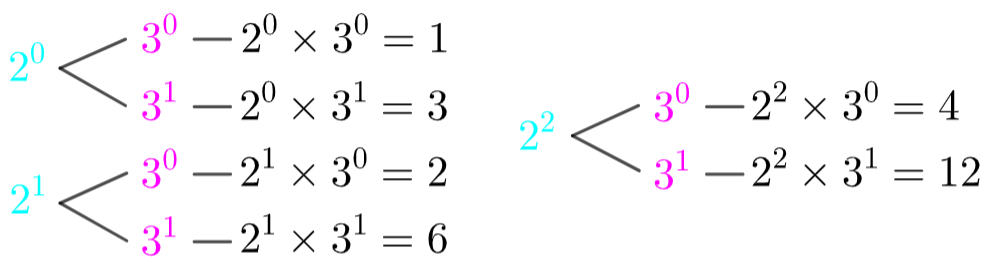
約数は素因数の組み合わせでしたから、約数の総和を次のように計算します。

\( \begin{aligned} (\color{deepskyblue}{2^0}×3^0)+(\color{deepskyblue}{2^0}×3^1)+(\color{hotpink}{2^1}×3^0)+(\color{hotpink}{2^1}×3^1)+(\color{lime}{2^2}×3^0)+(\color{lime}{2^2}×3^1) \ \end{aligned} \)

\( \begin{aligned} =\color{deepskyblue}{2^0}×(3^0+3^1)+\color{hotpink}{2^1}×(3^0+3^1)+\color{lime}{2^2}×(3^0+3^1) \end{aligned} \)

\( \begin{aligned} =(\color{deepskyblue}{2^0}+\color{hotpink}{2^1}+\color{lime}{2^2})(3^0+3^1) \end{aligned} \)

\( \begin{aligned} =7×4 \end{aligned} \)

この求め方をまとめたものが次の公式です。

約数の総和

ある自然数が\(\color{deepskyblue}{〇^a}×\color{hotpink}{△^b}×\color{lime}{◻︎^c}\)と素因数分解できるとき、その約数の総和は

\( \begin{aligned} \color{deepskyblue}{(〇^0+〇^1+\cdots+〇^a)}\color{hotpink}{(△^0+△^1+\cdots+△^b)}\color{lime}{(◻︎^0+◻︎^1+\cdots+◻︎^c)} \end{aligned} \)

生徒

わざわざ約数を計算しなくても、公式を使えば簡単に求められるね！！

まとめ：約数の個数と総和

さん

さて、今回のまとめだよ！

約数の個数

ある自然数が\(\color{deepskyblue}{〇^a}×\color{hotpink}{△^b}×\color{lime}{◻︎^c}\)と素因数分解できるとき、その約数の個数は

\(\color{deepskyblue}{(a+1)}×\color{hotpink}{(b+1)}×\color{lime}{(c+1)}\)

約数の総和

ある自然数が\(\color{deepskyblue}{〇^a}×\color{hotpink}{△^b}×\color{lime}{◻︎^c}\)と素因数分解できるとき、その約数の総和は

\( \begin{aligned} \color{deepskyblue}{(〇^0+〇^1+\cdots+〇^a)}\color{hotpink}{(△^0+△^1+\cdots+△^b)}\color{lime}{(◻︎^0+◻︎^1+\cdots+◻︎^c)} \end{aligned} \)