【意味から分かる数A】順列の総数の求め方を例題でわかりやすく解説！

さん

今日の板書はこれ！

順列

異なる \(n\) 個のものの中から \(r\) 個を取り出し1列に並べる順列の総和は

\( \begin{aligned} \color{red}{_nP_r}&=\color{red}{n(n-1)(n-2)\cdots(n-r+1)}\\ \\ &=\color{lime}{\frac{n!}{(n-r)!}}\:(r≦n)\\ \\ \end{aligned} \)

\( \begin{aligned} 特に\:_nP_n&=\color{red}{n(n-1)(n-2)\cdots 3×2×1}\\ \\ &=\color{red}{n!}\\ \\ \end{aligned} \)

ただし、\(_nP_0=1, \: 0!=1\) と定める。

生徒

もっと詳しく願いします！！

現役教員として数学を教えている「さん」と申します。

「人より勉強に時間がかかる」と感じていませんか？

私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。

• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」

• 「解答の意味が理解できず、勉強が進まない」

教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。

でも大丈夫！

このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。

意味から理解し、噛み砕き方をマスターしましょう！！

勉強しても成績が上がらない3つの理由と現役教師が教えるたった1つの解決策

一生懸命やってるのに結果が出ない…そんな中高生の悩みを、現役教師が本気で解決！信頼できる家庭教師が導く正しい学び方とは？

順列
まとめ：順列

順列

順列の「数え方」と記号Pの「使い方」

さん

順列について次の例題を使って説明していくね！

例題

\(4\)人から \(3\)人を選んで\(1\)列に並べるとき、並べ方の総数を求めよ。

順列の「数え方」

この問題のように、異なる \(n\) 個のものの中から \(r\) 個を取り出し１列に順番に並べる順列の総数を考えていきます。

簡単にいうと、選んで並べるのが順列です。

まずは、樹形図を使って数えていきましょう。

４人をそれぞれA、B、C、Dと名前を付けて、３人並べます。

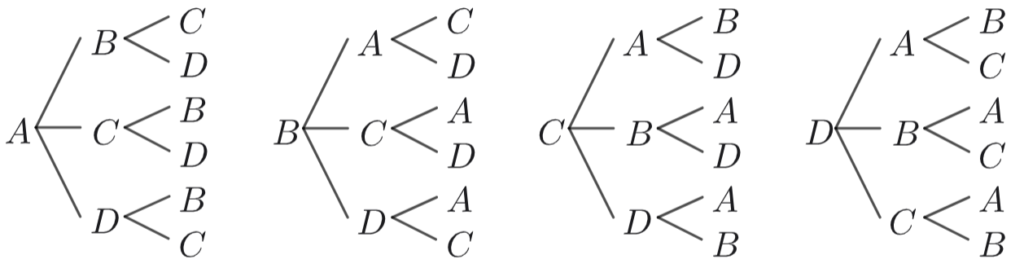
この樹形図から、\(24\)通りと数えることができますね。

これを、「積の法則」を使ってもう少し賢く数えてみましょう。

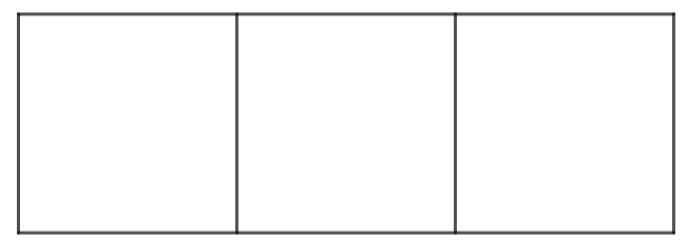
上の図は、３人を並べる場所です。

まずは、左の場所について考えます。

左にはA、B、C、Dの４人が並ぶ可能性がありますので、４通りの並び方があります。

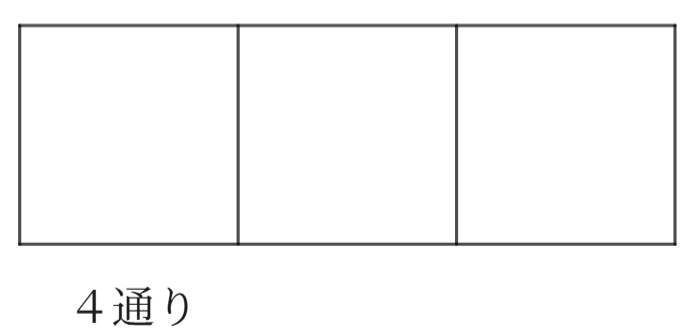
次に、真ん中の場所について考えます。

真ん中には、左に並べた人以外の３人が並ぶことができます。

左の４通りそれぞれに対して、３通りの並び方があります。

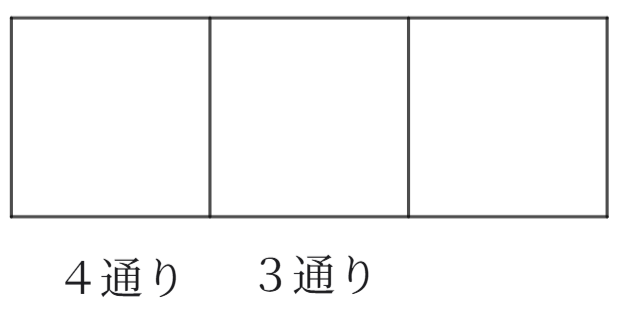
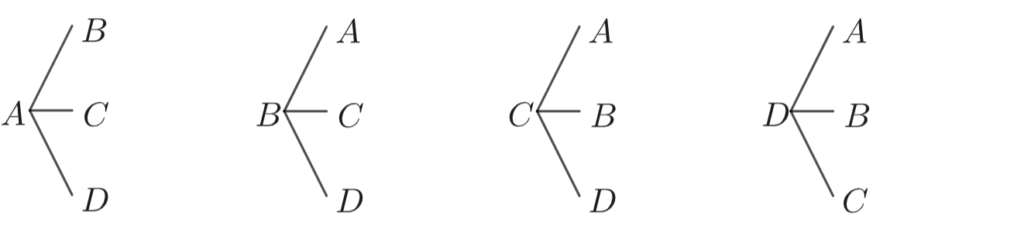
最後に、右の場所について考えます。

右には、今までに並べた人以外の２人が並ぶことができます。

真ん中の３通りそれぞれに対して、２通りの並び方があります。

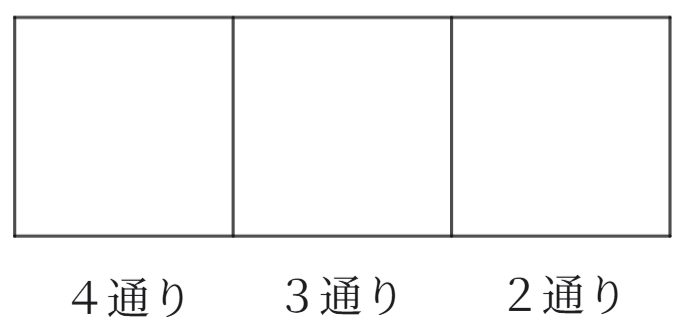
まとめると、「左に並ぶ４通り」に対して「真ん中に３通り」の並び方があり、さらに「右に２通り」の並び方があるわけです。

「積の法則」を使うと、\(4×3×2=24\) 通りと数えることができるのです。

これが、順列の数え方です。

生徒

なるほど！「選んで並べるときは樹形図をイメージして積の法則」だね！

記号Pの「使い方」

４人から３人選んで並べる総数を「\(_4 P _3\) 」と表すことができ、「ヨンピーサン」と読みます。

つまり、「\(_4 P _3=4×3×2=24\) 」です。

また、「\(_4 P _0\) 」は「４人から０人を選んで並べる総数」のことを指してしまうことになりますが、この値は「\(1\) 」と定めることにしてあります。

「\(_5 P _0\) 」も「\(_6 P _0\) 」も「\(_{10} P _0\) 」も「\(1\) 」です。

さん

これをまとめたものが下の公式だけど、順列は公式に当てはめるのではなく、樹形図をイメージしようね！

順列

異なる \(n\) 個のものの中から \(r\) 個を取り出し1列に並べる順列の総和は

\( \begin{aligned} \color{red}{_nP_r}&=\color{red}{n(n-1)(n-2)\cdots(n-r+1)}\:(r≦n)\\ \\ \end{aligned} \)

ただし、\(_nP_0=1\) と定める。

階乗

さん

次は選んだものを全部並べる総数を数えるよ！

例題

\(7\)人を１列に並べるときの並べ方の総数を求めよ。

階乗の「数え方」

この例題では７人全員を並べたときの総数を求めます。

並べる場所を用意しました。

左から順に並べると、７通り、６通り、５通り、・・・、２通り、１通りの並ばせ方があります。

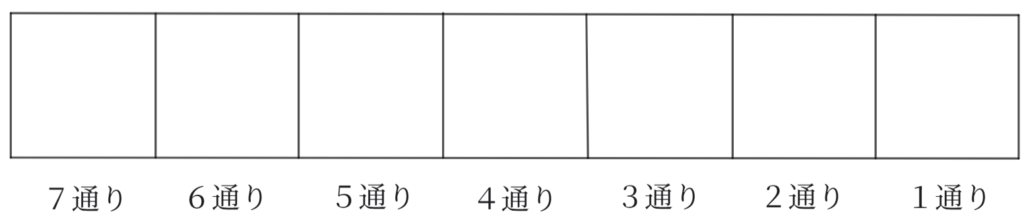
よって、積の法則を使うと次のように計算することができます。

\(7×6×5×4×3×2×1=5040\) 通り

さん

ここまでは、理解できるかな？

生徒

理解できた！！けど、\(7×6× \cdots ×1\)って書くの大変だね。

７人全員を並べる総数を「\(7!\)」と表すことができ、「ナナの階乗」と読みます。

つまり、「\(7!=7×6×5×4×3×2×1=5040\)」です。

生徒

おっ。だいぶ簡単に表せるね！！

階乗の「使い方」

階乗の計算はよく出てきますので、\(3!\) から \(6!\) までを暗記することで計算が楽になります。

\(3!=6,\:4!=24,\:5!=120,\:6!=720\) ここまでは暗記しておきましょう。

これを暗記していれば、 \(7!\) を次のように計算することができます。

\(7!=7×6!=7×720=5040\)

生徒

なるほど！\(10!\) は、\(10!=10×9×8×7×6!\) ってことだね！

さん

覚えられる人は、\(7!\) も覚えておくと楽になるね！

また、「\(0!\) 」は「0人全員を並べる総数」のことを指してしまうことになりますが、この値は「\(1\) 」と定めることにしてあります。

順列

\( \begin{aligned} 特に\:_nP_n=\color{red}{n(n-1)(n-2)\cdots 3×2×1}=\color{red}{n!}\\ \\ \end{aligned} \)

ただし、\(_nP_0=1, \: 0!=1\) と定める。

順列の階乗表現

さん

「\(_nP_r\)」を「\(!\)」を使った表し方があるから紹介するね！

\( \begin{aligned} \color{red}{_7P_3}&=\color{lime}{\frac{7!}{4!}}\\ \\ &=\frac{7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1}{ 4\cdot 3\cdot 2\cdot 1}\\ \\ &=7\cdot 6\cdot 5\\ \\ \end{aligned} \)

\( \begin{aligned} \color{red}{_{10}P_8}&=\color{lime}{\frac{10!}{2!}}\\ \\ &=\frac{10\cdot 9\cdot 8\cdot 7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1}{ 2\cdot 1} \\ \\ &=10\cdot 9\cdot 8\cdot 7\cdot 6\cdot 5\cdot 4\cdot 3\\ \\ \end{aligned} \)

\( \begin{aligned} \color{red}{_nP_r}=\color{lime}{\frac{n!}{(n-r)!}}\\ \\ \end{aligned} \)

「一旦全員並べておいて、後で辻褄を合わせるために余分なやつを割ってやる」という考え方です。

まとめ：順列

さん

さて、今回のまとめだよ！

順列

異なる \(n\) 個のものの中から \(r\) 個を取り出し1列に並べる順列の総和は

\( \begin{aligned} \color{red}{_nP_r}&=\color{red}{n(n-1)(n-2)\cdots(n-r+1)}\\ \\ &=\color{lime}{\frac{n!}{(n-r)!}}\:(r≦n)\\ \\ \end{aligned} \)

\( \begin{aligned} 特に\:_nP_n&=\color{red}{n(n-1)(n-2)\cdots 3×2×1}\\ \\ &=\color{red}{n!}\\ \\ \end{aligned} \)

ただし、\(_nP_0=1, \: 0!=1\) と定める。

生徒

ありがとうございました！！

【塾で成績が上がらない】「家庭教師」が効果的な３つの理由とは？

塾に通っても成績が伸びない…そんな悩みに寄り添うのが「家庭教師」という選択肢。現役高校教師の体験と共に、東大家庭教師友の会の魅力を解説します。完全個別対応・学習の見える化・やる気サポートの3つの理由から、塾に代わる学びの方法を紹介。無料体験の流れや料金情報も丁寧に掲載！

↑前の記事↑

↑次の記事↑

【数学A】場合の数04：順列