
今日の板書はこれ!
隣接するものは、1組にまとめて全体を並べた後、組の中を並べる。
大人 \(4\)人と子ども \(3\)人が \(1\)列に並ぶとき、子どもが \(3\)人続く並び方は何通りあるか。
大人 \(4\)人と子ども \(3\)人 \(1\)組の並べ方は \(5!=120\)
子ども \(3\)人の並べ方は \(3!=6\)
よって、 \(120×6=720\) 通り

もっと詳しく願いします!!
現役教員として数学を教えている「さん」と申します。
「人より勉強に時間がかかる」と感じていませんか?
私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。
• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」
• 「解答の意味が理解できず、勉強が進まない」
教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。
でも大丈夫!
このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。
意味から理解し、噛み砕き方をマスターしましょう!!
隣り合う並び方の数え方

次の例題を考えてみよう!
大人 4人と子ども3人が1列に並ぶとき、子どもが3人続く並び方は何通りあるか。
素直に考える。
子どもが3人続く並び方は、次の5通りがあります。
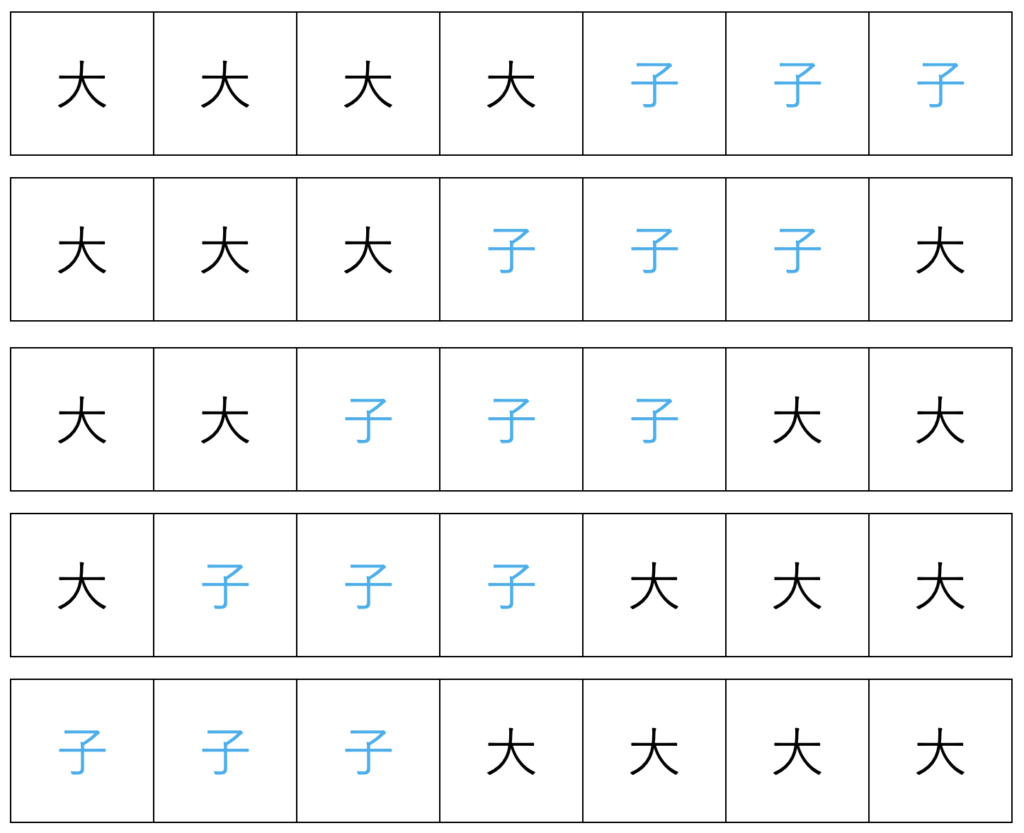

これでおしまい?

ううん。大人4人(A,B,C,D)と子ども3人(a,b,c)はそれぞれ区別して考えてあげようね!
そして、この5通りそれぞれに対して、大人(A,B,C,D)が \(4!\) 通り、子ども(a,b,c)が \(3!\) 通りの並び方があります。
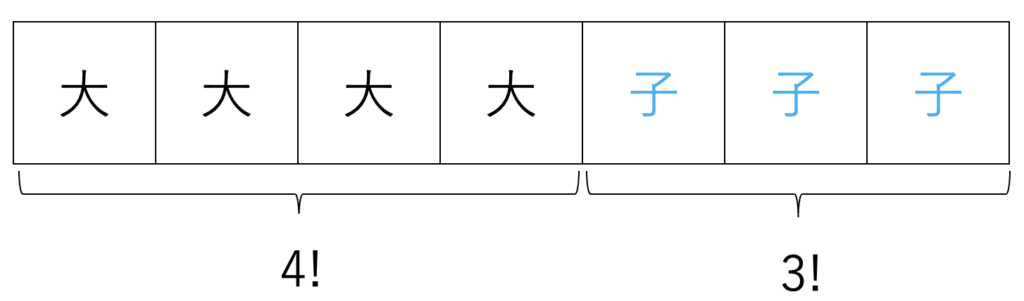
よって、求める場合の数は \(5×4!×3!=720\) 通りと計算することができます。

なるほどね!!こうやって数えるんだ!

理解できてえらい!!

ところで、最初の5通りは自分で書き出さないと分からないの?

おお!いいところに気づいたね!!
答えを導くことはできましたが、「最初の5通りは自分で数えないといけない」という欠点があります。

問題が複雑になったら数えるの大変になっちゃいそうだね。
工夫して考える。
隣接する順列は、次のように考えるのがセオリーです。
隣接するものは、1組にまとめて全体を並べた後、組の中を並べる。
今回の例題での登場人物は大人4人(A,B,C,D)と子ども3人(a,b,c)で、隣接するものは子どもの 3人でした。

まず、子ども3人を1組にまとめます。

そして、大人4人と子ども1組を並べます。
この並べ方は、\(5!\) 通り。
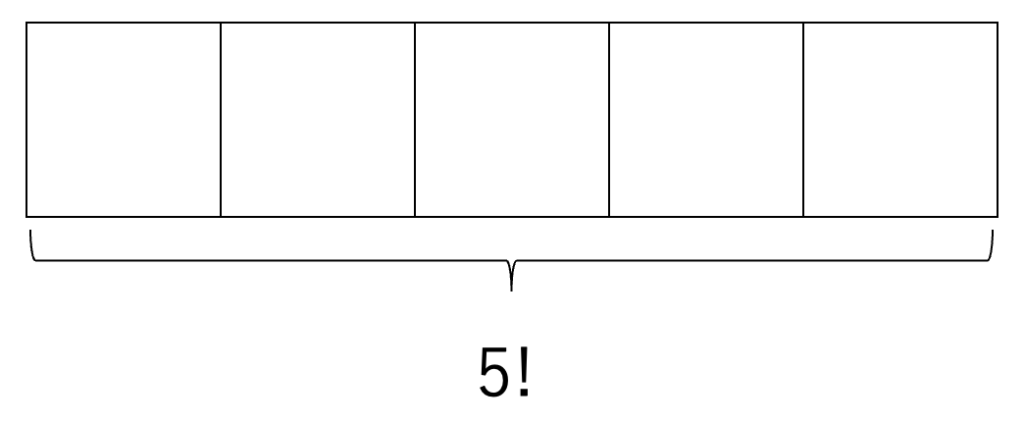
最後に、\(5!\) 通りそれぞれに対して、組の中の子どもを並べます。

この並べ方は、\(3!\) 通り。
よって、\(5!×3!=720\) 通り と計算することができます。

おー!これの考え方だと、自分で数えなくてもできるね!

隣接する順列はこうやって考えよう!
まとめ:隣り合う並び方の総数

さて、今回のまとめだよ!
隣接するものは、1組にまとめて全体を並べた後、組の中を並べる。
大人 \(4\)人と子ども \(3\)人が \(1\)列に並ぶとき、子どもが \(3\)人続く並び方は何通りあるか。
大人 \(4\)人と子ども \(3\)人 \(1\)組の並べ方は \(5!=120\)
子ども \(3\)人の並べ方は \(3!=6\)
よって、 \(120×6=720\) 通り

ありがとうございました!!






コメント