
今日の板書はこれ!
- 最高位に\(0\)がくると桁数が減る
- 条件の強い位から順に処理していく
6個の数字 0, 1, 2, 3, 4, 5 のうち異なる4個を並べて、4桁の整数をつくるとき、次のような整数は何個つくれるか。
(1) 4桁の整数
千の位の数字は0以外の5通りがある
残りの位は、5個の数字から3個を選んで並べる順列である
よって \(5×_5P_3=5×5×4×3=300\) 通り
(2) 2桁の奇数
一の位は、1, 3, 5 の3通りがある
また、十の位は0と一の位を除く4通りである
よって \(3×4=12\) 通り

もっと詳しく願いします!!
現役教員として数学を教えている「さん」と申します。
「人より勉強に時間がかかる」と感じていませんか?
私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。
• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」
• 「解答の意味が理解できず、勉強が進まない」
教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。
でも大丈夫!
このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。
意味から理解し、噛み砕き方をマスターしましょう!!
数字の順列

数字の順列を次の例題で考えよう!
6個の数字 0, 1, 2, 3, 4, 5 のうち異なる4個を並べて、4桁の整数をつくるとき、次のような整数は何個つくれるか。
(1) 4桁の整数
次の場所に 0, 1, 2, 3, 4, 5 の中から選んで並べます。
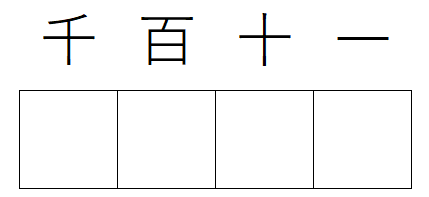
注意すべき点は、最上位桁が0になった場合、その桁は位として扱われず桁数が減るということです。
たとえば、0, 1, ,2, 3 を選んで次のように並べると「0123」という整数になりますが、これは4桁ではなく、3桁の整数として扱われます。

ですから、千の位に入れれる数字は0以外の5通り(1~5)となります。
一の位から百の位は、千の位の数字以外の5個から3個選んで並べればよいので\(_5P_3\) 通りと数えることができます。
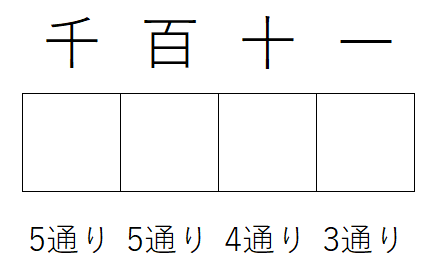
よって、4桁の整数は \(5×_5P_3=5×5×4×3=300\) 通りと考えることができます。

最上位に0はきちゃダメってことだね!

いいね!もう1問考えてみよう!
6個の数字 0, 1, 2, 3, 4, 5 のうち異なる4個を並べて、4桁の整数をつくるとき、次のような整数は何個つくれるか。
(2) 2桁の奇数
次の場所に 0, 1, 2, 3, 4, 5 の中から選んで並べます。
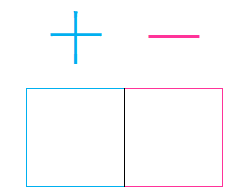
(1) と同様に、十の位には0を並べることはできないので、1, 2, 3, 4, 5の 5通りを並べることができます。
また、奇数を作るためには、一の位が奇数でなければいけないので、1, 3, 5の 3通りを並べることができます。

じゃあ \(5×3=15\) 通りだ!!

ぶっぶー。それは間違いだよ!!
樹形図で考えてみましょう。

十の位に1, 3, 5を使ったときは一の位は2通りですが、十の位に2, 4を使ったときは一の位は3通りです。
十の位の5通りそれぞれに対して一の位が3通りあるのであれば \(5×3=15\) 通りで間違いないのですが、この樹形図では積の法則は使えません。
そこで、重要な考え方が、条件の強い位から順に処理していくという考え方です。
今回は「0を使ってはいけない」という条件と「奇数しか使ってはいけない」という条件がありますが、どちらのほうが強い条件でしょうか。

んー「奇数しか使ってはいけない」かな…?

そのとおり!!
条件の強い一の位を考えたあとに十の位を考えます。
一の位は、1, 3, 5の 3通り。
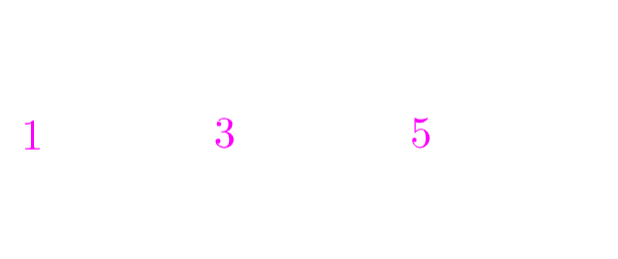
そして、そのそれぞれに対して、十の位に並べるのは4通り。
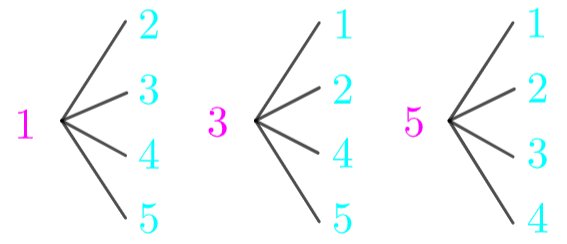
この樹形図のだと、積の法則が使えますね。
よって、 \(3×4=12\) 通り。

なんとなく掛けるのかな?ってやったら間違えちゃうね。

積の法則を使うときは樹形図をイメージしようね。
まとめ:数字の順列

さて、今回のまとめだよ!
- 最高位に\(0\)がくると桁数が減る
- 条件の強い位から順に処理していく
6個の数字 0, 1, 2, 3, 4, 5 のうち異なる4個を並べて、4桁の整数をつくるとき、次のような整数は何個つくれるか。
(1) 4桁の整数
千の位の数字は0以外の5通りがある
残りの位は、5個の数字から3個を選んで並べる順列である
よって \(5×_5P_3=5×5×4×3=300\) 通り
(2) 2桁の奇数
一の位は、1, 3, 5 の3通りがある
また、十の位は0と一の位を除く4通りである
よって \(3×4=12\) 通り

ありがとうございました!!






コメント