
今日の板書はこれ!
異なる\(n\)個のものから重複を許して\(r\)個取って並べる順列の総数は \(n^r\)

もっと詳しく願いします!!
現役教員として数学を教えている「さん」と申します。
「人より勉強に時間がかかる」と感じていませんか?
私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。
• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」
• 「解答の意味が理解できず、勉強が進まない」
教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。
でも大丈夫!
このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。
意味から理解し、噛み砕き方をマスターしましょう!!
重複順列
考え方

次の例題を使って考えよう!
記号〇と×を、重複を許して5個並べる。このとき、並べ方は何通りあるか。
次の5つの場所に「〇」か「×」のどちらかを入れていきます。
今までの順列では、選んだものをもう1度選ぶことはできませんでしたが、今回の問題では、何回も選ぶことができます。
このような順列を、重複順列といいます。
5つの場所は、それぞれ「〇」か「×」の2通りの並べ方あるので、総数は次のように計算することができます。
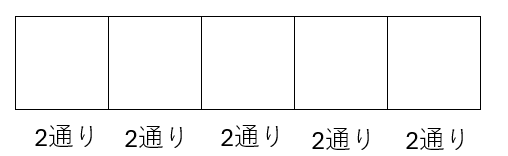
\(2×2×2×2×2=32\) 通り

重複順列だったら、公式 \(n^r\) に当てはめる…。

その覚え方はダメ~!!重複順列は公式を覚える必要はないよ!ただ、「積の法則」を使うだけ!
「順列」と「重複順列」の違い

なんか問題を解いてると、「順列」なのか「重複順列」なのかわからなくなっちゃった。

次の例題で比較してみよう!
次の場合は何通りあるか求めよ。
(1) A, B, C の3文字の中から、異なる2文字を並べる。
(3) A, B, C の3文字から、同じ文字を繰り返してもよいとき、2文字を並べる。
順列は「並べる」とき、重複順列は「何回も使っていいものを並べる」ときの考え方です。
(1) は「異なる2文字を並べる」ので、\(3 \cdot 2=6\)通り。
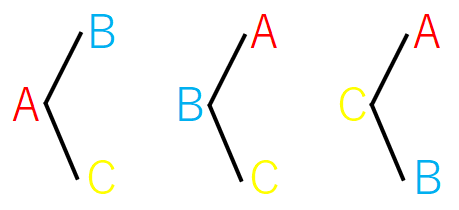
(2) は「同じ文字を繰り返してもよいとき、2文字を並べる」ので、\(3\cdot 3=9\)通り。
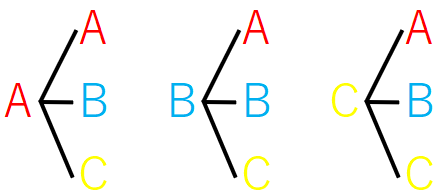

問題文に「並べる」ってあったら「P」を使う!みたいな仕組みを理解してない解き方はやめようね。

問題の本質を理解できるように勉強しないと!!
まとめ:重複順列

さて、今回のまとめだよ!
異なる\(n\)個のものから重複を許して\(r\)個取って並べる順列の総数は \(n^r\)

ありがとうございました!!






コメント