
今日の板書はこれ!
同じものがそれぞれ\(p\)個、\(q\)個ずつ、全部で\(n\)個ある。
この\(n\)個のものをすべて並べる順列の総数は\(\displaystyle _nC_p=\frac{n!}{p!q!}\)

もっと詳しく願いします!!
現役教員として数学を教えている「さん」と申します。
「人より勉強に時間がかかる」と感じていませんか?
私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。
• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」
• 「解答の意味が理解できず、勉強が進まない」
教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。
でも大丈夫!
このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。
意味から理解し、噛み砕き方をマスターしましょう!!
同じものを含む順列

次の例題で考えよう!
「A」2個と「B」3個の並び方は何通りあるか。
同じものを含む順列(組合せ)
A, A, B, B, B を並べる順列を考えます。
もしすべての文字が異なる A, B, C, D, E であれば、並べ方は \(5!\) 通りです。
しかし今回のように、A が2個、B が3個ある場合、それぞれは同じ文字なので区別ができません。
「並べる」といっても、区別できないもの同士は順番を入れ替えても同じ並び方になります。
つまり、実際には「どの位置に A を置くか」を選ぶだけでよいのです。
5つの位置の中から、A を置く2か所を選び、残りの位置に B を入れることで、すべての並び方が決まります。
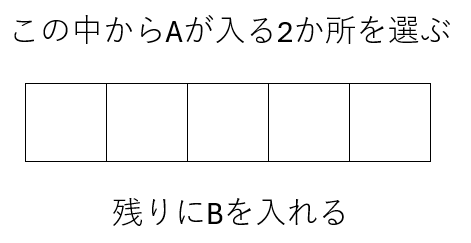
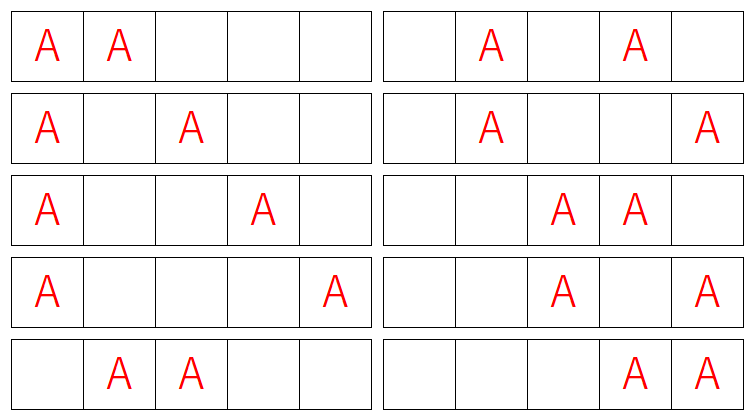
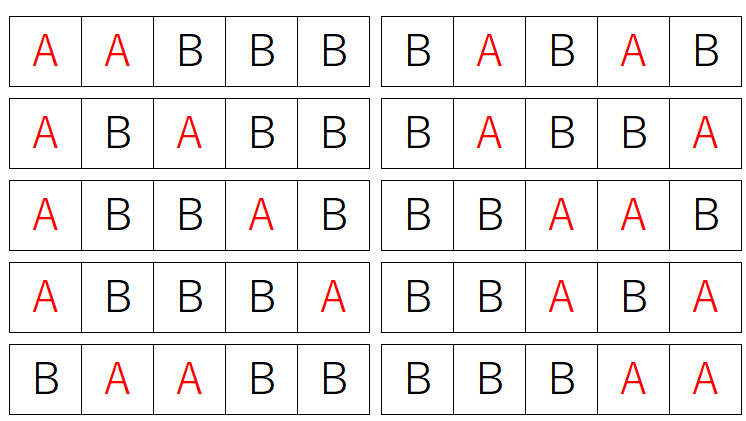
\(_5C_2= 10\) 通り
同じものを含む順列(階乗)
階乗を使った求め方もマスターしましょう。
まず、5個の文字を \(A_1, A_2, B_1, B_2, B_3\) して、すべて区別できるものと考えます。
このときの並べ方は \(5!\) 通りです。
しかし実際には、A 同士・B 同士は区別できません。
同じ並びが何度も数えられてしまっているので、それを取り除く必要があります。
A の並び替えは \(2!\) 通り、B の並び替えは \(3!\) 通りあるため、\(\displaystyle\frac{5!}{2!3!}=10\) 通りとなります。

なるほど…でもまだちょっとピンとこないかも。

よし、具体的に見てみよう!
たとえば、すべてを区別して \(A_1, A_2, B_1, B_2, B_3\) 並べた中には、次のような12通りの並べ方が存在します。

しかし、この12通りは実際には区別できないため、次のようになります。


えっ、全部同じ並び方になっちゃう!?
\(A_1\) と \(A_2\) の並び順 、 \(B_1\) と \(B_2\) と \(B_3\) の並び順は、それぞれ区別できないもののため、 1通りの扱いとなります。
ですから、重複している \(2!3!\)通りで割ってあげる必要があるのです。

なぜ割るのか理解できたかな?
まとめ:区別のない組合せ

さて、今回のまとめだよ!
同じものがそれぞれ\(p\)個、\(q\)個ずつ、全部で\(n\)個ある。
この\(n\)個のものをすべて並べる順列の総数は\(\displaystyle _nC_p=\frac{n!}{p!q!}\)

ありがとうございました!!






コメント