【数学A】場合の数14：最短経路の総数

---

---

現役教員として数学を教えている「さん」と申します。

「人より勉強に時間がかかる」と感じていませんか？

私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。

教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。

でも大丈夫！

このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。

意味から理解し、噛み砕き方をマスターしましょう！！

同じものを含む順列

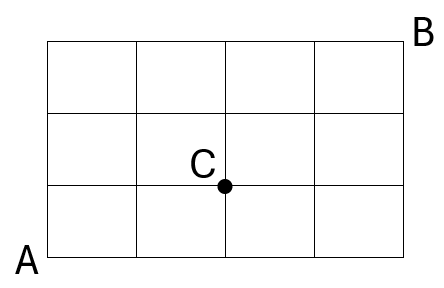
(1) AからBまで行く。

AからBまで行く道順には、例えば次のような行き方があります。

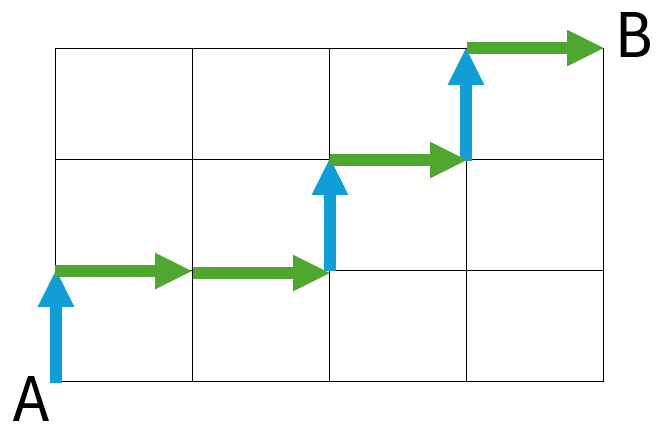
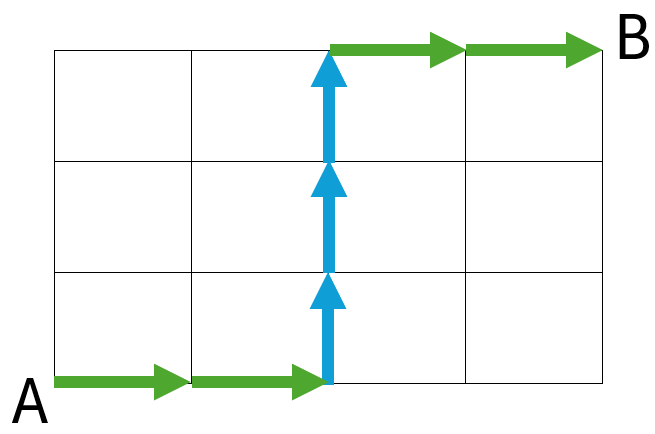
1つ目の図は「↑→→↑→↑→」と移動し、2つ目の図は「→→↑↑↑→→」と移動します。

どの経路をたどる場合でも、右方向（→）に4回、上方向（↑）に3回動くことになります。

したがって、最短経路の総数は「→を4個、↑を3個並べる並べ方」として考えることができます。

これは 同じものを含む順列 の考え方です。

よって、\(\displaystyle\frac{7!}{4!3!}=35\)

(2) AからCを通ってBまで行く。

AからCを通ってBまで行く道順には、次のような行き方があります。

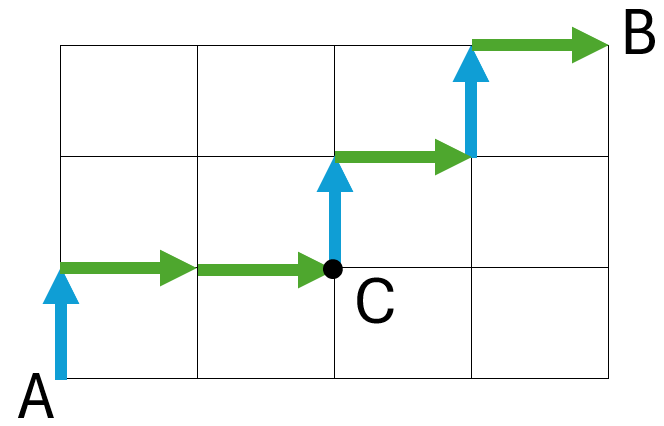
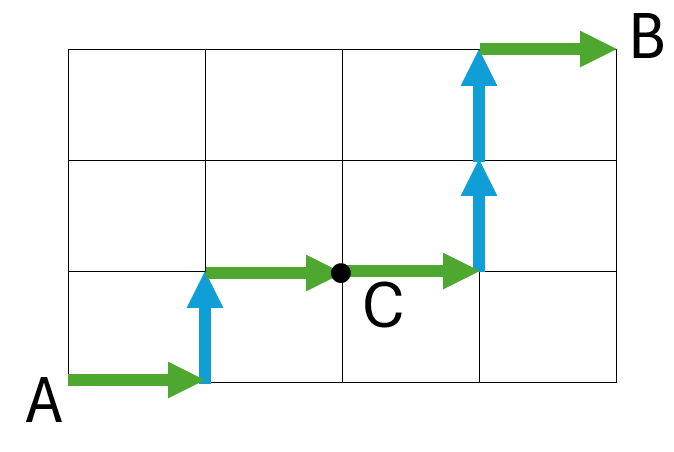
まず、AからCまでの最短経路を考えます。

このとき、右方向（→）に2回、上方向（↑）に1回動くので、同じものを含む順列の総数は\(\displaystyle\frac{3!}{2!}\)通りとなります。

次に、CからBまでの最短経路を考えます。

ここでは、右方向（→）に2回、上方向（↑）に2回動くため、同じものを含む順列の総数は\(\displaystyle\frac{4!}{2!2!}\)通りです。

したがって、AからCを通ってBまで行く道順の総数は、\(\displaystyle\frac{3!}{2!}×\frac{4!}{2!2!}=18\)通りとなります。

(3) AからCを通らずにBまで行く。

AからCを通らずにBまで行く道順を考えます。

このように「～でない」といった否定の言葉が出てきたときは、補集合を使って考えると、計算がぐっと楽になります。

\((Cを通らない)=(全体)-(Cを通る)\)

(1) より、AからBまで行く全体の道順は 35 通り。

(2) より、AからCを通ってBまで行く道順は 18 通り。

したがって、AからCを通らずにBまで行く道順は次のように求められます。

\(35-18=17\)通り

まとめ：最短経路の総数

---

---