【数学A】確率01：確率の定義

---

---

現役教員として数学を教えている「さん」と申します。

「人より勉強に時間がかかる」と感じていませんか？

私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。

教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。

でも大丈夫！

このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。

意味から理解し、噛み砕き方をマスターしましょう！！

確率の定義

試行と事象

この例題では、「箱から玉を1個取り出す」ことを考えます。

その結果として起こりうるすべての可能性の中から、［赤玉を取り出す］割合を求めるのが確率です。

このように「玉を1個取り出す」行為を試行といい、「玉を赤玉取り出す」などの結果を事象と呼びます。

同様に確からしいとは

(1)では、「白玉2個と赤玉2個」が入った箱から玉を1個取り出します。

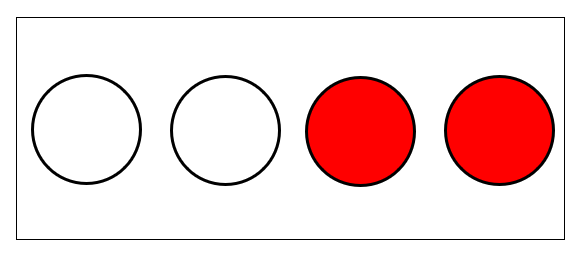
ここで、起こりうるすべての場合を整理して考えてみましょう。

このとき、「白玉を取り出す」と「赤玉を取り出す」の2通りが考えられます。

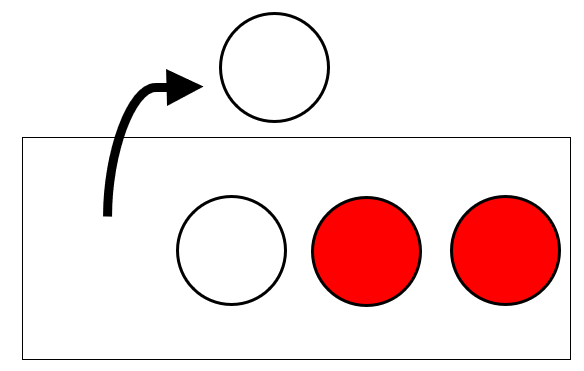
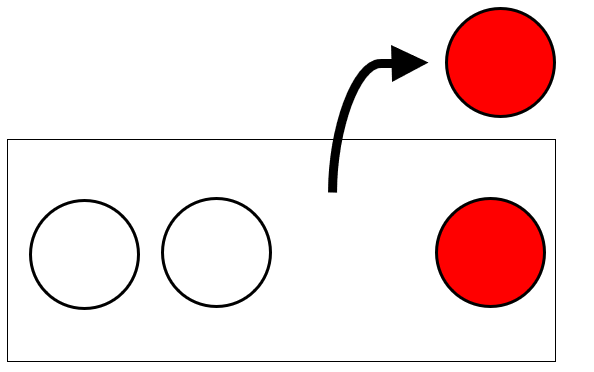
したがって、［赤玉を取り出す］確率は、\(\displaystyle\frac{［赤玉］}{［白玉］［赤玉］}=\frac{1}{2}\)

---

(2) では、「白玉1個と赤玉3個」が入った箱から玉を1個取り出します。

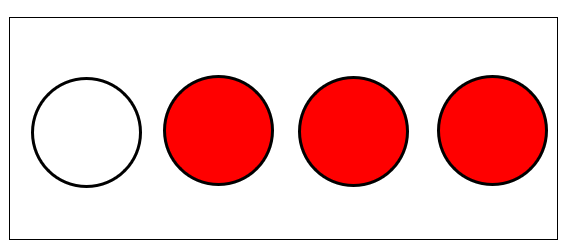
(1)と同じように、起こりうるすべての場合を「白玉を取り出す」と「赤玉を取り出す」の2通りと考えてみましょう。

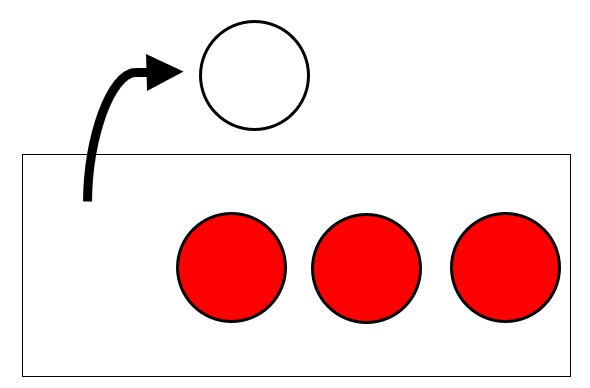
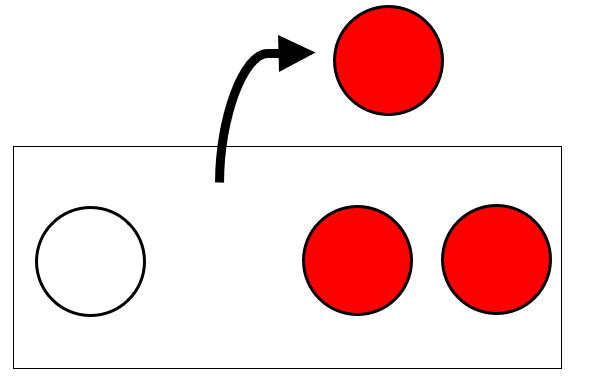
このとき、［赤玉を取り出す］確率は、\(\displaystyle\frac{［赤玉］}{［白玉］［赤玉］}=\frac{1}{2}\)

ここで、確率を考えるうえでの重要なポイントを確認します。

それは、「同様に確からしい（＝同程度に起こりやすい）事象で考える」です。

(1) のように「白玉2個と赤玉2個」の場合、白玉を引くのも赤玉を引くのも同じくらい起こりやすいので、両者は同様に確からしい事象といえます。

しかし、(2) のように「白玉1個と赤玉3個」の場合、赤玉を引くほうが明らかに起こりやすく、同じとはいえません。

つまり、(2)では『同様に確からしい』とは言えないのです。

---

ここで、確率を考えるうえでのもう1つの重要なポイントがあります。

それは「確率は同じモノでも区別して考える」ということです。

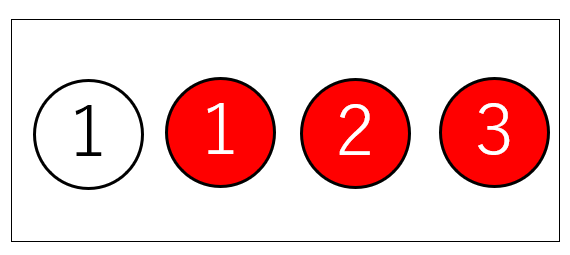
「白玉1個と赤玉3個」が入った箱を、
［白玉］・［赤玉1］・［赤玉2］・［赤玉3］のように、1つずつ区別して考えます。

「白玉1個と赤玉3個」を［白玉］［赤玉1］［赤玉2］［赤玉3］と考えると、どれが選ばれても同じ条件（＝同様に確からしい事象）になります。

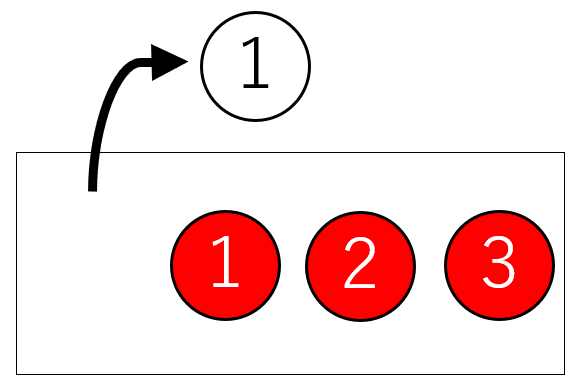
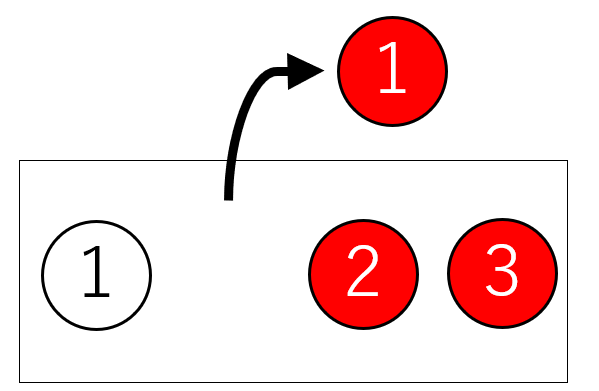
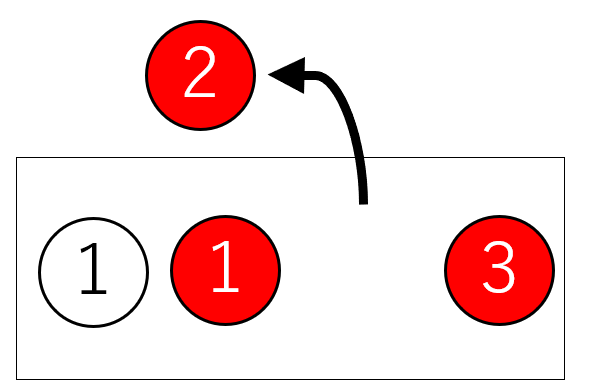
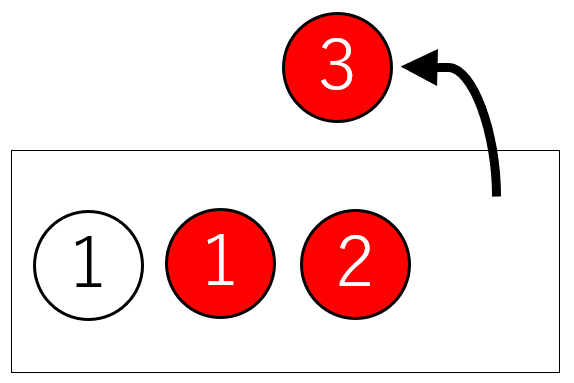
したがって(2)の正しい答えは、\(\displaystyle\frac{［赤玉1］［赤玉2］［赤玉3］}{［白玉］［赤玉1］［赤玉2］［赤玉3］}=\frac{3}{4}\)

(1) 「白玉2個と赤玉2個」の場合、どちらの考え方も正しく、同様に確からしい。

〇　\(\displaystyle\frac{［赤玉］}{［白玉］［赤玉］}=\frac{1}{2}\)

〇　\(\displaystyle\frac{［赤玉1］［赤玉2］}{［白玉1］［白玉2］［赤玉1］［赤玉2］}=\frac{2}{4}=\frac{1}{2}\)

(2) 「白玉1個と赤玉3個」の場合、下のように区別して考えるのが正しい。

×　\(\displaystyle\frac{［赤玉］}{［白玉］［赤玉］}=\frac{1}{2}\)

〇　\(\displaystyle\frac{［赤玉1］［赤玉2］［赤玉3］}{［白玉］［赤玉1］［赤玉2］［赤玉3］}=\frac{3}{4}\)

まとめ：確率の定義

---

---