【数学A】確率02：確率を求める手順

---

---

現役教員として数学を教えている「さん」と申します。

「人より勉強に時間がかかる」と感じていませんか？

私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。

教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。

でも大丈夫！

このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。

意味から理解し、噛み砕き方をマスターしましょう！！

確率を求める手順

手順１：全事象を決める

まず、「全事象（すべての起こりうる場合）」をどう取るかを決めましょう。

確率は 「同様に確からしい事象」 をもとに考える必要があります。

つまり、全事象の取り方は複数あっても構いません。

次のような取り方が考えられます。

それぞれの全事象の数は次の通りです。

---

「7個の文字列（同じ文字を区別）の並べ方」であれば \(7!\)通り。

---

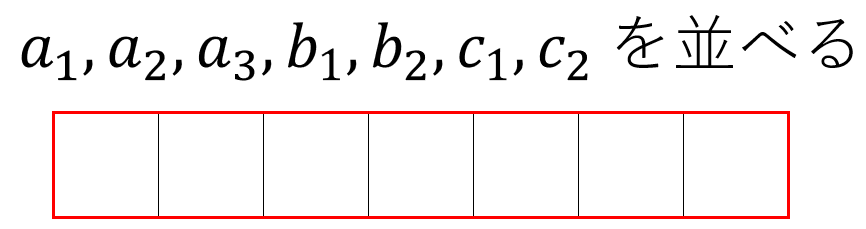
「7個の文字列（同じ文字を区別しない）の並べ方」であれば \(\displaystyle\frac{7!}{3!2!2!}\)通り

---

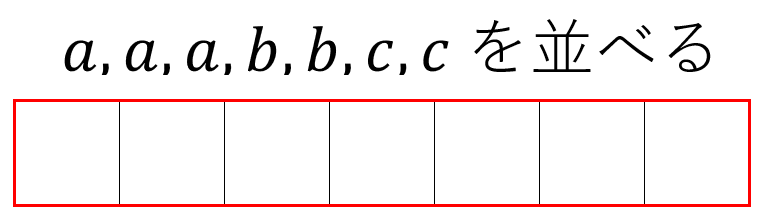
「両端に並ぶ文字（同じ文字を区別）の並べ方」であれば \(_7P_2\)通り

---

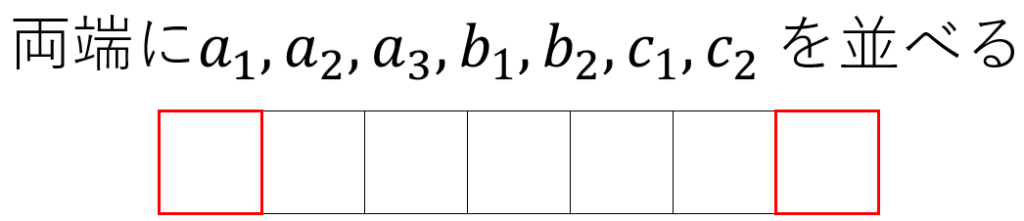
「\(c\) が並ぶ場所（同じ文字を区別しない）の組合せ」であれば \(_7C_2\)通り

---

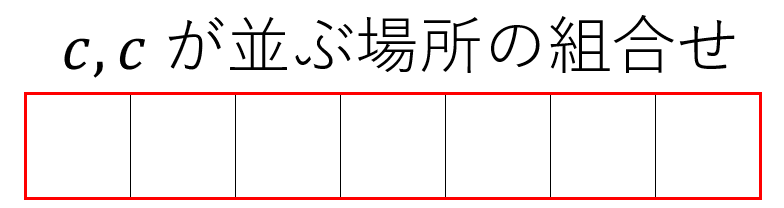
どの方法で考えても、「同様に確からしい事象」であれば正しい確率を求めることができます。

では次のような取り方はどうでしょう？

「両端に並ぶ文字（同じ文字を区別しない）の並べ方」は、

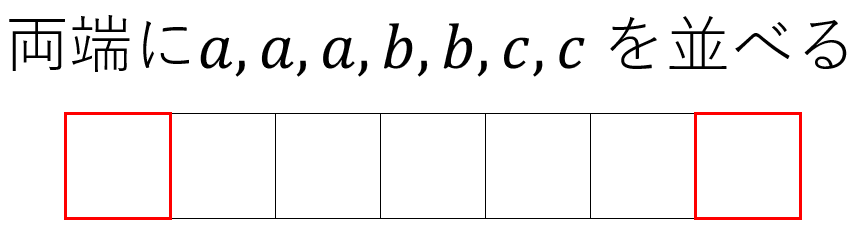
左端にくる文字は \(a, b, c\) の3通、右端も \(a, b, c\) の3通りなので、\(3×3=9\)通り。

次の2つの並べ方は「起こりやすさ」が同じになっていません。

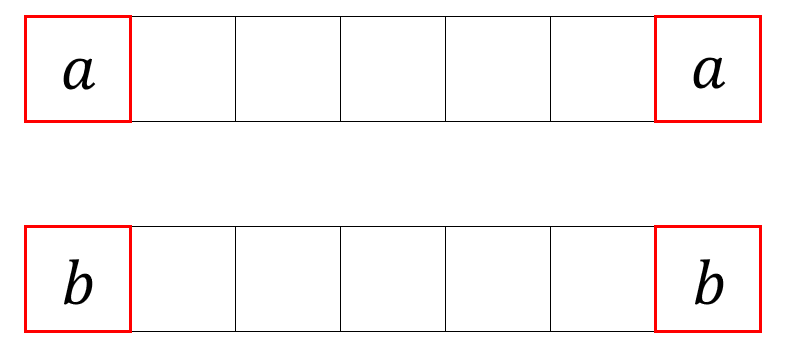
両端が\(a\)の方が、両端が\(b\)よりも多く出現しやすいのです。

つまり、「同様に確からしい」 という条件を満たしていません。

手順２：同じ基準で事象Aを数える

次に、手順①で決めた全事象の基準と同じ基準で、「両端が \(c\) となる」場合（事象A）を数えていきましょう。

---

全事象を「7個の文字列（同じ文字を区別）の並べ方」の \(7!\)通りとするなら、

「両端が \(c\) となる」のは、両端の並べ方が\(c_1, c_2\)の順列 \(2!\)通りであり、残りの並べ方が\(a_1, a_2, a_3, b_1, b_2\)の順列 \(5!\)通り。

したがって、確率は\(\displaystyle \frac{2!×5!}{7!}=\frac{2!×5!}{7×6×5!}=\frac{1}{21}\)

---

全事象を「7個の文字列（同じ文字を区別しない）の並べ方」の \(\displaystyle\frac{7!}{3!2!2!}\)通りとするなら、

「両端が \(c\) となる」のは、両端の並べ方が\(c, c\)を並べる \(1\)通りであり、残りの並べ方が\(a, a, a, b, b\)の同じものを含む順列 \(\displaystyle \frac{5!}{3!2!}\)通り。

したがって、確率は\(\displaystyle \frac{1×\frac{5!}{3!2!}}{\frac{7!}{3!2!2!}}=\frac{5!2!}{7!}=\frac{2!×5!}{7×6×5!}=\frac{1}{21}\)

---

全事象を「両端に並ぶ文字（同じ文字を区別）の並べ方」の \(_7P_2\)通りとするなら、

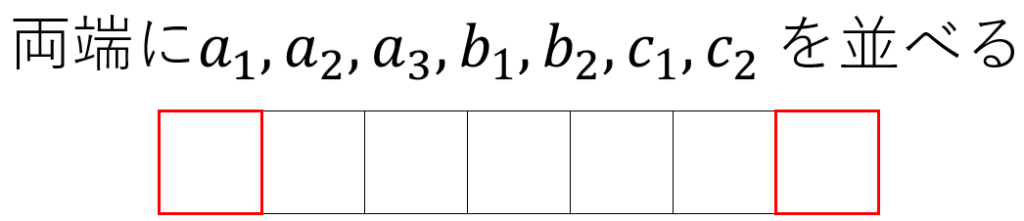
「両端が \(c\) となる」のは、両端の並べ方が\(c_1, c_2\)を入れる \(2!\)通り。

したがって、確率は\(\displaystyle \frac{2!}{_7P_2}=\frac{2}{7×6}=\frac{1}{21}\)

---

全事象を「\(c\) が並ぶ場所（同じ文字を区別しない）の組合せ」の \(_7C_2\)通りとするなら、

「両端が \(c\) となる」のは、両端の並べ方が\(c, c\)を並べる \(1\)通り。

したがって、確率は\(\displaystyle \frac{1}{_7C_2}=\frac{1}{\frac{7×6}{2×1}}=\frac{1}{21}\)

---

まとめ：事象Aの起こる確率を求める手順

---

---