【数学A】確率05：独立試行の確率

---

---

現役教員として数学を教えている「さん」と申します。

「人より勉強に時間がかかる」と感じていませんか？

私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。

教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。

でも大丈夫！

このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。

意味から理解し、噛み砕き方をマスターしましょう！！

独立試行の確率

今回は「事象Aかつ事象Bが起こる確率」を求めていきます。

「AかつB」が起こる確率は、それぞれの確率を掛け合わせることで求めることができます。

一方、「AまたはB」が起こる確率は、それぞれの確率を足すことで求めました（確率の加法定理）。

この「足す」と「掛ける」を混同してしまう生徒がとても多いです。

そこで今回は、どんなときに足し算・掛け算を使うのかを、例題を通してしっかり理解していきましょう。

例題

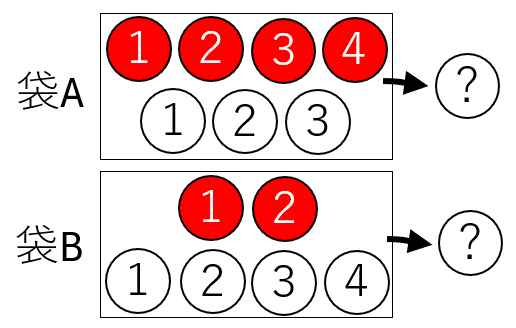
Step 1：事象を分けて考える

「A・Bの袋から同じ色の玉を取り出す」事象は、次の2つに分けられます。

• 両方とも赤を取り出す
• 両方とも白を取り出す

それぞれの確率を順に求めていきましょう。

Step 2：「両方とも赤を取り出す確率」

まずは、「両方とも赤を取り出す確率」を求めます。

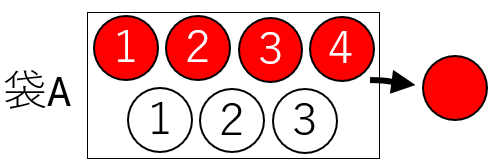
Aの袋から赤玉を取り出す確率は、\(\displaystyle \frac{3}{5}\)

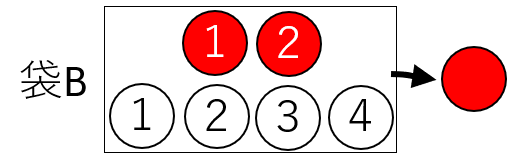
Bの袋から赤玉を取り出す確率は、\(\displaystyle \frac{2}{6}\)

正解は、「掛ける」です。

「両方とも赤を取り出す確率」は、「Aの袋から赤玉を取り出す」かつ「Bの袋から赤玉を取り出す」こと。

このように、両方の事象が同時に起こらなければならないときは、確率を掛けて求めます。

よって、「両方とも赤を取り出す確率」は、\(\displaystyle \frac{3}{5}×\frac{2}{6}\)

Step 3：「両方とも白を取り出す確率」

Aの袋から白玉を取り出す確率は、\(\displaystyle \frac{2}{5}\)

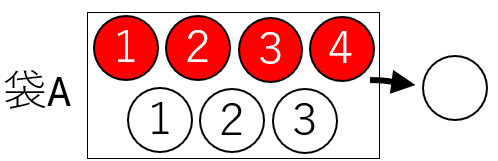
Bの袋から白玉を取り出す確率は、\(\displaystyle \frac{4}{6}\)

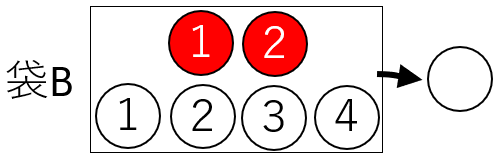
したがって、\(\displaystyle \frac{2}{5}×\frac{4}{6}\)

Step 4：「A・Bの袋から同じ色の玉を取り出す確率」

正解は、「足す」です。

「A・Bの袋から同じ色の玉を取り出す確率」は、「両方とも赤」または「両方とも白」。

このように、両方の事象のうちどちらかが起こればよいときは、確率を足して求めます。

したがって、\(\displaystyle \frac{3}{5}×\frac{2}{6}+\frac{2}{5}×\frac{4}{6}=\frac{7}{15}\)

振り返り

求めたいのは「A・Bの袋から同じ色の玉を取り出す確率」でしたね。

この確率は、「両方とも赤を取り出す確率」と「両方とも白を取り出す確率」の2つに分けて考えました。

「A・Bの袋から同じ色の玉を取り出す確率」は、「両方とも赤」を取り出してもいいし、「両方とも白」を取り出してもOKです。

つまり、どちらが起きても大丈夫なときは「足す」です。

一方で、「両方とも赤を取り出す確率」は、「Aの袋から赤玉を取り出す」かつ「Bの袋から赤玉を取り出す」必要があります。

つまり、どちらも起きないといけないときは「掛ける」です。

独立な試行

2つの確率を掛けるときには、それぞれの試行が独立でなければなりません。

「独立」とは？

試行が独立とは、試行の結果が互いに影響しないことをいいます。

今回の問題では、「Aの袋から玉を取り出す」試行と「Bの袋から玉を取り出す」試行が独立です。

Aの結果がBの結果に影響を与えないので、確率を掛けて求めることができました。

独立でない試行の例

では、独立でないのはどんな場合でしょうか。

たとえば「Aの袋から2個の玉を取り出す」場合を考えてみましょう。

1個目を取り出し、その玉をもとに戻さずに2個目を取り出すと、1個目の結果によって、2個目の状況（残りの玉の色の割合）が変わってしまいます。

つまり、1回目の結果が2回目に影響しているため、この2つの試行は独立ではありません。

まとめ：確率の加法定理

---

---