
今日の板書はこれ!
同じ条件で同じ試行を繰り返すとき、各回の試行は互いに独立である。このような独立な試行を何度も行うことを反復試行という。
試行を \(n\) 回繰り返すとき、事象Aが \(r\) 回起こる確率は、\(_nC_rp^n(1-p)^{n-r}\)で表せる。

もっと詳しく願いします!!
現役教員として数学を教えている「さん」と申します。
「人より勉強に時間がかかる」と感じていませんか?
私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。
• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」
• 「解答の意味が理解できず、勉強が進まない」
教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。
でも大丈夫!
このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。
意味から理解し、噛み砕き方をマスターしましょう!!
反復試行の確率
例題1:反復試行の問題に触れる

次の例題を考えよう!
1個のさいころを3回続けて投げるとき、6の目がちょうど2回出る確率を求めよ。
この問題では、「さいころを投げる」という同じ試行を3回繰り返しています。
このように、同じ条件で同じ試行を繰り返し行うことを反復試行といいます。
今回は、この反復試行の確率について、詳しく考えていきましょう。
3回中2回6の目がでる状況の確認
「6の目が出る」事象を〇、「6の目が出ない」事象を×とします。
このとき、3回のうちちょうど2回「6の目が出る」場合は、次の3通りがあります。
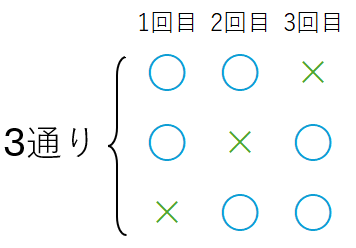
[〇〇×]の確率
「6の目が出る」確率は \(\displaystyle \color{Blue}{\frac{1}{6}}\)、「6の目が出ない」確率は \(\displaystyle \color{green}{1-\frac{1}{6}=\frac{5}{6}}\)です。
したがって[〇〇×]となる確率は、\(\displaystyle \color{Blue}{\frac{1}{6}}×\color{Blue}{\frac{1}{6}}× \color{green}{\frac{5}{6}}=\color{Blue}{\left(\frac{1}{6}\right)^2}× \color{green}{\left(\frac{5}{6}\right)^1}\)
[〇×〇]の確率
同様に、[〇×〇]となる確率は、\(\displaystyle \color{Blue}{\frac{1}{6}}× \color{green}{\frac{5}{6}}×\color{Blue}{\frac{1}{6}}=\color{Blue}{\left(\frac{1}{6}\right)^2}× \color{green}{\left(\frac{5}{6}\right)^1}\)
[×〇〇]の確率
また、[×〇〇]となる確率も、\(\displaystyle \color{green}{\frac{5}{6}} ×\color{Blue}{\frac{1}{6}}×\color{Blue}{\frac{1}{6}}=\color{Blue}{\left(\frac{1}{6}\right)^2}× \color{green}{\left(\frac{5}{6}\right)^1}\)
3回中2回6の目がでる確率を求める

あれ?3通りとも、確率は全部同じなんだね。

とってもいい気づき!じゃあ、ここで問題。
これらの確率は「足す」と「掛ける」、どっちかな?
「3回中2回6の目が出る」ときは、[〇〇×]でも[〇×〇]でも[×〇〇]でもOKなので、それぞれの確率を足して求めます。
例題2:反復試行の問題を一般化する
反復試行の考え方を一般化し、より効率よく確率を求められるようにしましょう。
まず、先ほどの例題を振り返ります。
1個のさいころを3回続けて投げるとき、6の目がちょうど2回出る確率を求めよ。
「3回のうち、ちょうど2回6の目が出る」のは、次の3通りでした。
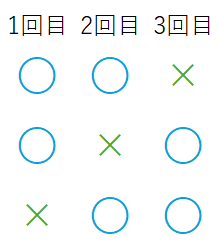
この3通りは「3回のうち2回が〇になる並べ方の数」です。
つまり、「〇が2個、×が1個の同じものを含む順列」の総数 \(_3C_2\)通りです。
そして、それぞれの確率は \(\displaystyle \color{Blue}{\left(\frac{1}{6}\right)^2}× \color{green}{\left(\frac{5}{6}\right)^1}\)
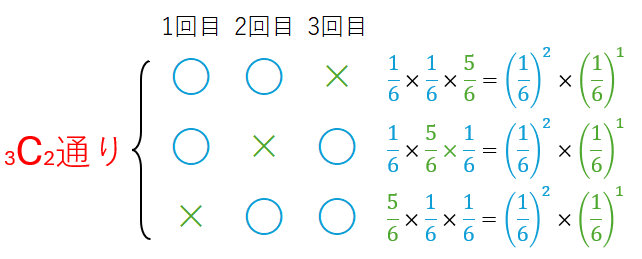
したがって、\(_3C_2\)通りすべてを足し合わせて求めると、
\(\displaystyle\color{red}{_3C_2}× \color{Blue}{\left(\frac{1}{6}\right)^2}× \color{green}{\left(\frac{5}{6}\right)^1}=\frac{5}{72}\)

さいころを投げる回数を増やして考えてみよう!
1個のさいころを5回続けて投げるとき、6の目がちょうど2回出る確率を求めよ。
「5回のうち、ちょうど2回6の目が出る」のは、「〇が2個、×が3個の同じものを含む順列」の総数 \(_5C_2\)通り。
それぞれの確率は、\(\displaystyle \color{Blue}{\left(\frac{1}{6}\right)^2}× \color{green}{\left(\frac{5}{6}\right)^3}\)
したがって、\(\displaystyle\color{red}{_5C_2}×\color{Blue}{\left(\frac{1}{6}\right)^2}× \color{green}{\left(\frac{5}{6}\right)^3}=\frac{625}{3888}\)

これを一般化すると、次のように表すことができるよ!
試行を \(n\) 回繰り返すとき、事象Aが \(r\) 回起こる確率は、\(_nC_rp^n(1-p)^{n-r}\)で表られる。
例題3:反復試行の応用問題を考える
赤玉3個、白玉2個の入った袋から玉を1個取り出し、色を見てからもとにものどす。この試行を5回行うとき、5回目に3度目の赤玉が出る確率を求めよ。

6個から1個を取り出す試行を5回行うから、反復試行の問題だね!
「5回目に3度目の赤玉が出る」というのは、「4回目までに赤玉が2回でて、5回目に3回目の赤玉が出る」ことを意味します。
4回のうちに赤玉がちょうど2回出る並べ方は、「〇が2個、×が2個の同じものを含む順列」の総数 \(_4C_2\)通りです。
それぞれの確率は、\(\displaystyle \color{Blue}{\left(\frac{4}{6}\right)^2}× \color{green}{\left(\frac{2}{6}\right)^2 }×\color{Blue}{\frac{4}{6}}\)
したがって、\(\displaystyle\color{red}{_4C_2}×\color{Blue}{\left(\frac{4}{6}\right)^2}× \color{green}{\left(\frac{2}{6}\right)^2 }×\color{Blue}{\frac{4}{6}}=\frac{16}{81}\)
まとめ:反復試行の確率

さて、今回のまとめだよ!
同じ条件で同じ試行を繰り返すとき、各回の試行は互いに独立である。このような独立な試行を何度も行うことを反復試行という。
試行を \(n\) 回繰り返すとき、事象Aが \(r\) 回起こる確率は、\(_nC_rp^n(1-p)^{n-r}\)で表せる。

ありがとうございました!!






コメント