【数学A：確率】条件付き確率をわかりやすく解説！問題通して理解しよう！

さん

今日の板書はこれ！

条件付き確率

事象Aが起こったときに事象Bが起こる確率（条件付き確率）を\(P_A(B)\)で表す。
\(n(A)≠0,\:P(A)≠0\)のとき\(\displaystyle P_A(B)=\frac{n(A\cap B)}{n(A)}=\frac{P(A\cap B)}{P(A)}\)

生徒

もっと詳しく願いします！！

現役教員として数学を教えている「さん」と申します。

「人より勉強に時間がかかる」と感じていませんか？

私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。

• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」

• 「解答の意味が理解できず、勉強が進まない」

教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。

でも大丈夫！

このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。

意味から理解し、噛み砕き方をマスターしましょう！！

勉強しても成績が上がらない3つの理由と現役教師が教えるたった1つの解決策

一生懸命やってるのに結果が出ない…そんな中高生の悩みを、現役教師が本気で解決！信頼できる家庭教師が導く正しい学び方とは？

条件付確率
1. 例題
まとめ：条件付き確率

条件付確率

事象Aが起こったという前提のもとで、事象Bが起こる確率を条件付き確率といい、\(P_A(B)\)で表します。

多くの生徒が、条件付き確率\(P_A(B)\)と\(P(A\cap B)\)を混同しがちです。

ここでは、その違いをわかりやすく解説します。

さん

次の例題で解説するよ！

例題

例題１

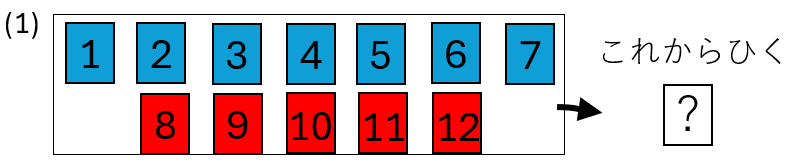
箱の中に1から7までの青色の番号札7枚と、8から12までの赤色の番号札5枚が入っている。
(1) この箱から番号札を1枚引くとき、その札が青色の偶数である確率を求めよ。
(2) この箱から番号札を1枚引いたとき、その札は青色であった。その札が偶数である確率を求めよ。

(1) AかつBの確率

例題１

箱の中に1から7までの青色の番号札7枚と、8から12までの赤色の番号札5枚が入っている。
(1) この箱から番号札を1枚引くとき、その札が青色の偶数である確率を求めよ。

まず、箱の中の札を整理してみましょう。

青色の札：奇数が 4枚（1,3,5,7）、偶数が 3枚（2,4,6）
赤色の札：奇数が 2枚（9,11）、偶数が 3枚（8,10,12）

ここで、「青色の札である」という事象をA、「偶数の札である」という事象をBとします。

求めたいのは、「青色かつ偶数の札を引く確率」\(=\color{red}{P(A\cap B)}\)です。

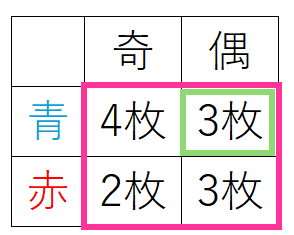
分母（全体）は「12枚の札から1枚を引く」ので 12通り。

分子は「青色かつ偶数を引く」ので 3通り。

したがって、\(\displaystyle\color{red}{ P(A\cap B)}=\frac{\color{green}{3}}{\color{hotpink}{12}}=\frac{1}{4}\)

(2) Aが起きたときBが起こる確率

例題１

箱の中に1から7までの青色の番号札7枚と、8から12までの赤色の番号札5枚が入っている。
(2) この箱から番号札を1枚引いたとき、その札は青色であった。その札が偶数である確率を求めよ。

求めたいのは「青色を引いたという条件のもとで、その札が偶数である確率」

つまり、\(\color{red}{ P_A(B)}\)です。

(1) では、「12 枚の中から青色かつ偶数の札を引く確率」すなわち、\(\color{red}{P(A\cap B)}\)を求めました。

一方、(2) では 「青色である」ことがすでにわかっている 状況です。

条件付き確率は、条件によって全体（分母）が絞られます。

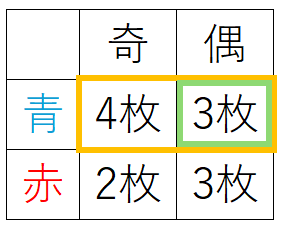
全体（分母）は「青色の札7枚から1枚を引く」ので 7通り。

分子は「青色の札の中で偶数を引く」ので 3通り。

したがって、\(\displaystyle\color{red}{ P_A(B)}=\frac{\color{green}{3}}{\color{gold}{7}}\)

生徒

つまり、条件付き確率って、全体の取り方が変わるってこと？

さん

その通り！
条件付き確率では、「条件の中だけ」を新しい全体として考えるんだ。

(2)を確率 ÷ 確率で求める。

例題１

条件付き確率は \(\displaystyle\frac{\text{確率}}{\text{確率}}\) つまり、\(\displaystyle\color{red}{ P_A(B)}=\frac{\color{green}{P(A\cap B)}}{\color{gold}{P(A)}}\) で求めることができます。

求めたいのは、「青色を引いたという条件のもとで、その札が偶数である確率」。

したがって、\(\displaystyle \color{red}{ P_A(B)}=\frac{\color{green}{\text{青色かつ偶数の札である確率}}}{\color{gold}{\text{青色の札である確率}}}\)を求めます。

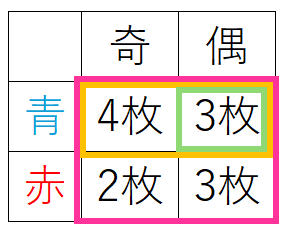
分母「青色の札である確率」は、\(\displaystyle\color{gold}{P(A)}=\frac{\color{gold}{7}}{\color{hotpink}{12}}\)

分子「青色かつ偶数の札である確率」は、\(\displaystyle\color{green}{P(A\cap B)}=\frac{\color{green}{3}}{\color{hotpink}{12}}\)

したがって、\(\displaystyle\color{red}{ P(A\cap B)}=\frac{\color{green}{P(A\cap B)}}{\color{gold}{P(A)}}=\frac{\frac{\color{green}{3}}{\color{hotpink}{12}}}{\frac{\color{gold}{7}}{\color{hotpink}{12}}}=\frac{\color{green}{3}}{\color{gold}{7}}\)