
今日の板書はこれ!
\(P(A\cap B)=P(A)P_A(B)\)

もっと詳しく願いします!!
現役教員として数学を教えている「さん」と申します。
「人より勉強に時間がかかる」と感じていませんか?
私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。
• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」
• 「解答の意味が理解できず、勉強が進まない」
教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。
でも大丈夫!
このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。
意味から理解し、噛み砕き方をマスターしましょう!!
確率の乗法定理
独立試行の確率では、2つの試行が互いに影響しない場合に\(P(A\cap B)=P(A)P(B)\)が成り立つことを確認しました。
しかし、2つの試行が独立でない場合は、同じようには求められません。
そのときに使うのが、確率の乗法定理です。
確率の乗法定理では、次の式を使って求めます。
\(P(A\cap B)=P(A)P_A(B)\)
つまり、「AとBが同時に起こる確率」は「Aが起こる確率」 ×「Aが起こったときにBが起こる確率」で求めることができます。
条件付き確率「Aが起こったときにBが起こる確率」と、確率の乗法定理「AかつBが起こる確率」の違いが分からなくなる生徒はよくいます。
例題を通して、両者の関係を整理しながら確認してみましょう。

次の例題で考えてみよう!
条件付確率と確率の乗法定理の見分け方と違い
当たりくじ4本を含む10本のくじを、A,Bの2人がこの順に1本ずつ引く。ただし、引いたくじは元に戻さない。
(1) Aが当たったとき、Bが当たる確率を求めよ。
(2) A,Bの2人とも当たる確率を求めよ。
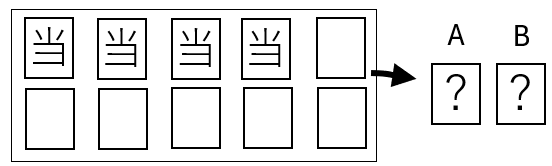
(1) Aが当たったとき、Bが当たる確率
(1)は、「Aが当たったという条件のもとで、Bが当たる確率」を求める問題です。
つまり、条件付確率 \(\color{green}{ P_A(B)}\) を求めることになります。
Aがすでに1本の当たりくじを引いているため、残りは「当たりくじ3本・はずれくじ6本」の9本。
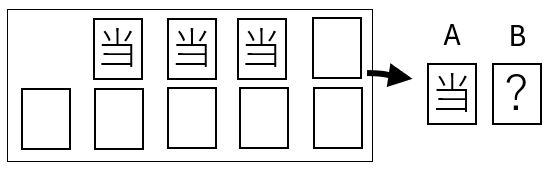
したがって、「Aが当たったとき、Bが当たる確率」は \(\displaystyle \color{green}{ P_A(B)}=\frac{3}{9}=\frac{1}{3}\)
(2) A,Bの2人とも当たる確率
(2)は「Aが当たり、さらにBも当たる確率」を求める問題です。
つまり、2つの事象が同時に起こる確率 \(\color{gold}{P(A\cap B)}\) を求めます。
しかし、「AとBが同時に起こる確率」は、単純に「Aが当たる確率 × Bが当たる確率」では求められません。
なぜなら、「Aが引く」という試行と「Bが引く」という試行は独立ではない からです。
Aの結果がBの状況を変えてしまうため、Bの確率はAの結果に影響を受けます。
たとえば、
- Aが当たりを引いた場合:Bは「当たり3本・はずれ6本」の9本の中から引く。
- Aがはずれを引いた場合:Bは「当たり4本・はずれ5本」の9本の中から引く。

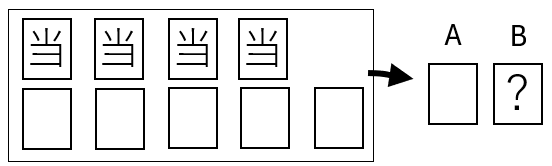
このように、Aの結果でBの確率が変化するため、確率の乗法定理を使って求めます。
確率の乗法定理は、\(\color{gold}{P(A\cap B)}=\color{blue}{P(A)}\color{green}{ P_A(B)}\) です。
つまり、「Aが当たる確率」 × 「Aが当たったときにBが当たる確率」で求められます。
「Aが当たる確率」は \(\displaystyle \color{blue}{P(A)}=\frac{4}{10}=\frac{2}{5}\)
「Aが当たったときにBが当たる確率」は(1)より \(\displaystyle \color{green}{P_A(B)}=\frac{1}{3}\)
したがって、
(1)条件付確率と(2)乗法定理の見分け方と違い

頭がごちゃごちゃになってきちゃった。

じゃあ、(1)と(2)をもう一度振り返ってみようか。
(1)は 「Aが当たったとき、Bが当たる確率」を求めました。
つまり、「Aが当たったという条件のもとで、Bが当たる確率」を求める問題です。
したがって、条件付き確率 \(\color{green}{ P_A(B)}\) を用いて求めます。
一方、(2)では「A,Bの2人とも当たる確率」を求めました。
これは「Aが当たり、さらにBも当たる」という、2つの事象が同時に起こる確率を求める問題です。
この場合は、確率の乗法定理 \(\color{gold}{P(A\cap B)}=\color{blue}{P(A)}\color{green}{ P_A(B)}\) を用いて求めます。
まとめると、
- 「〜が起こったときに〜が起こる」のは、条件付確率 \(\color{green}{ P_A(B)}\)
- 「AとBが同時に起こる」のは、乗法定理 \(\color{gold}{P(A\cap B)}=\color{blue}{P(A)}\color{green}{ P_A(B)}\)

おお!頭の中がすっきりした!!
追加問題

問題を追加したよ!この問題を考えて、確率の理解を深めよう!
当たりくじ4本を含む10本のくじを、A,Bの2人がこの順に1本ずつ引く。ただし、引いたくじは元に戻さない。
(3) Bが当たる確率を求めよ。
(4) Bが当たっとき、Aも当たっている確率を求めよ。
(3) Bが当たる確率
(2)で確認した通り、Aの結果がBの状況を変えてしまうため、「Bが当たる確率」はAの結果に影響を受けます。
- Aが当たりを引いた場合:Bは「当たり3本・はずれ6本」の9本の中から引く。
- Aがはずれを引いた場合:Bは「当たり4本・はずれ5本」の9本の中から引く。


したがって、「Bが当たる確率」は \(P(B)&=P(A\cap B)+P(\overline{A}\cap B)\) で表されます。
つまり、「A,Bの2人とも当たる確率」+「Aがはずれ、Bが当たる確率」で求めます。
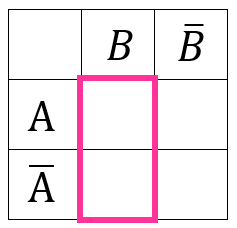
「A,Bの2人とも当たる確率」は (2) より
「Aがはずれ、Bが当たる確率」は
よって、「Bが当たる確率」は
(4) Bが当たっとき、Aも当たっている確率
「Bが当たったという条件のもとで、Aも当たっている確率」を求める問題です。
つまり、条件付確率 \(\color{purple}{ P_B(A)}\) を求めることになります。
しかし、Bが引くときのくじの状況は、Aの結果によって変わるため、
(1)のように直接「要素の個数」を数えることはできません。
そこで、確率÷確率 \(\displaystyle\color{purple}{P_B(A)}=\frac{\color{gold}{P(B\cap A)}}{\color{hotpink}{P(B)}}\) を使って求めます。
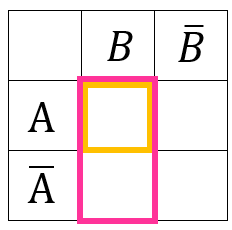
分母「Bが当たる確率」は、(3)より \(\displaystyle\color{hotpink}{P(B)}=\frac{2}{5}\)
分子「A,Bの2人とも当たる確率」は、(2)より \(\displaystyle\color{gold}{P(A\cap B)}=\frac{2}{15}\)
したがって、
まとめ:確率の乗法定理

さて、今回のまとめだよ!
\(P(A\cap B)=P(A)P_A(B)\)

ありがとうございました!!






コメント