【数学A：確率】期待値の求め方を簡単解説！例題で計算方法を学ぼう！

さん

今日の板書はこれ！

期待値

変数Xは、\(x_1,x_2,\cdots,x_n\) のうちどれか1つの値をとる。
また、その値をとる確率がそれぞれ\(P_1,P_2,\cdots,P_n\)である。（\(P_1+P_2+\cdots +P_n=1\)）
このとき、\(E(x)=x_1P_1+x_2P_2+\cdots+x_nP_n\)を変数Xの期待値という。

生徒

もっと詳しく願いします！！

現役教員として数学を教えている「さん」と申します。

「人より勉強に時間がかかる」と感じていませんか？

私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。

• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」

• 「解答の意味が理解できず、勉強が進まない」

教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。

でも大丈夫！

このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。

意味から理解し、噛み砕き方をマスターしましょう！！

勉強しても成績が上がらない3つの理由と現役教師が教えるたった1つの解決策

一生懸命やってるのに結果が出ない…そんな中高生の悩みを、現役教師が本気で解決！信頼できる家庭教師が導く正しい学び方とは？

期待値の求め方
1. 例題
まとめ：確率の乗法定理

期待値の求め方

期待値とは、「確率の重みをつけた平均値」のことです。

単純に平均を取るのではなく、「起こりやすさ（確率）」を考慮した平均を求めることで、より現実的な平均的な結果を表します。

さん

次の例題で考えてみよう！

例題

赤玉2個と青玉3個が入った袋から、2個の玉を同時に取り出し、出た赤玉1個につき1000円もらえるゲームがある。もらえる金額\(X\)の期待値\(E(X)\)を求めよ。また参加費が1000円のとき、このゲームに参加することは得であるといえるか。

このゲームでは、取り出した赤玉の数によってもらえる金額が次のように変わります。

赤玉0個　→　0円
赤玉1個　→　1000円
赤玉2個　→　2000円

一見すると「0円、1000円、2000円の平均は1000円だから、平均的には1000円もらえる」と思いがちです。

しかし、この3つの結果は同じ確率で起こるわけではありません。

各金額が出る確率を求める

0円（赤玉0個,青玉2個）の確率は、\(\displaystyle\frac{_3C_2}{_5C_2}=\frac{3}{10}\)

1000円（赤玉1個,青玉1個）の確率は、\(\displaystyle\frac{_2C_1×_3C_1}{_5C_2}=\frac{6}{10}\)

2000円（赤玉2個,青玉0個）の確率は、\(\displaystyle\frac{_2C_2}{_6C_3}=\frac{1}{10}\)

これをまとめた下の表を確率分布といます。

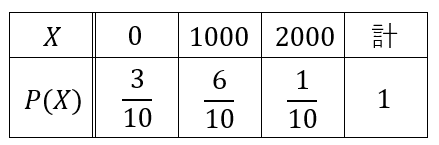
このように、1000円がもらえる確率が最も高く、2000円はめったに出ません。

したがって、単純な平均では「現実的な平均額」を表せないのです。

さん

約分は最後にした方が計算が楽になるよ！

期待値を求める

起こる確率を考慮した平均（＝期待値\(E(X)\)）は次の式で求められます。

\( \begin{aligned} \displaystyle E(x)&=0×\frac{3}{10}+1000×\frac{6}{10}+2000×\frac{1}{10}\\ \\ &=\color{hotpink}{\frac{0×3+1000×6+2000×1}{10}}\\ \\ &=800\\ \\ \end{aligned} \)