こんにちは、高校教員の『さん』です。今日は、「第2次導関数から極値を求める方法」について詳しく説明していくよ。
今回もよろしくお願いします！！
「人より勉強に時間がかかる」と感じていませんか？
私のクラスにも、同じ悩みを抱えて苦しんでいた生徒がたくさんいました。
• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」
• 「解答の意味が理解できず、勉強が進まない」
教科書の内容を理解するには、「自分で噛み砕いて考える力」が必要です。
このブログでは、よく寄せられる質問、つまずきやすいポイントをもとに、教科書の内容をわかりやすく解説していきます。
「噛み砕き方」がわかれば、文章はぐっと読みやすくなります！
まずは、教科書の説明を見てみましょう。
まずは教科書の説明
教科書ではこんなふうに説明されてるよ！
関数 \(f(x)\) の極値を判定するのに、第2次導関数 \(f^{\prime\prime}(x)\) を利用する方法がある。
\(f^{\prime\prime}(x)\) が連続関数であるとき、次のことが成り立つ。
- \(f'(a)=0\) かつ \(f^{\prime\prime}(a)>0\) ならば、\(f(a)\) は極小値である。
- \(f'(a)=0\) かつ \(f^{\prime\prime}(a)<0\) ならば、\(f(a)\) は極大値である。
【１の証明】 \(f^{\prime\prime}(a)>0\) のとき、\(a\) に十分近い \(x\) では \(f^{\prime\prime}(x)>0\) となり、\(f(x)’\) は増加する。
ここで、\(f'(a)=0\) であるから
\(x < a\) では \(f'(x) < 0\)
\(x > a\) では \(f'(x) > 0\)
よって、このとき \(f(a)\) は極小値である。
２についても、同様に証明することができる。
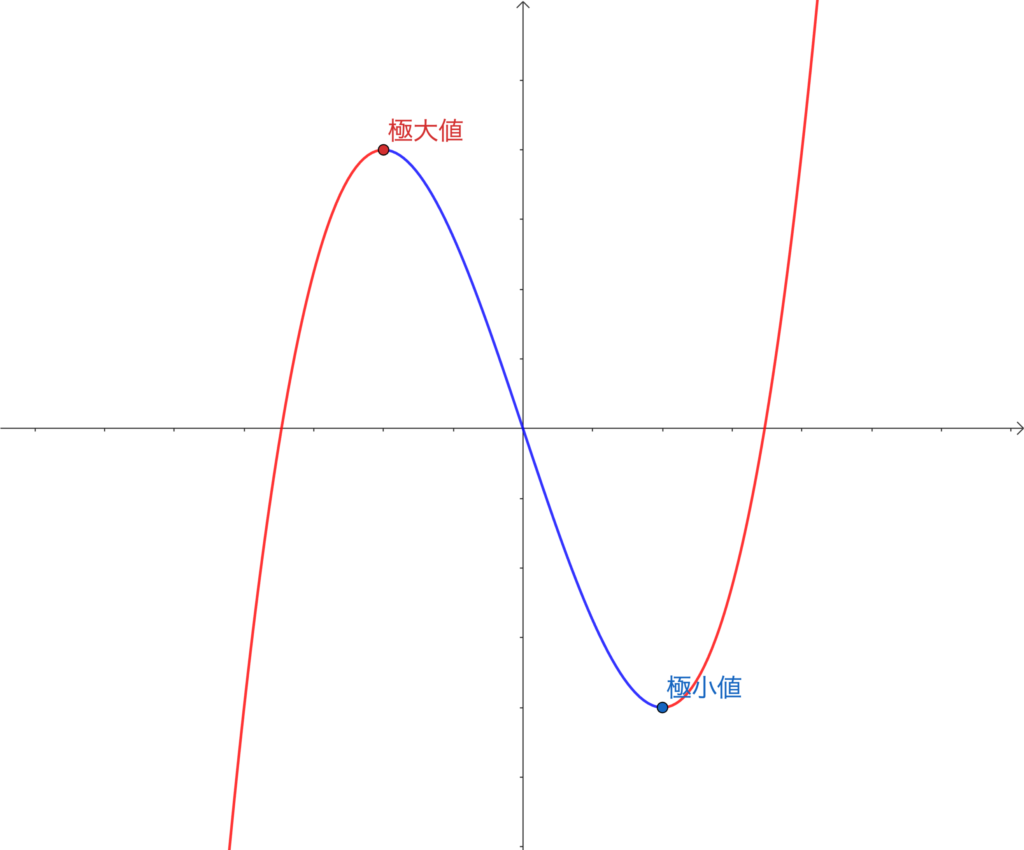
関数 \(f(x)=-x^3+3x\) の極値を、第２次導関数を利用して求めよ。
\(f'(x) = -3x^2 + 3\)、\(f^{\prime\prime}(x)=-6x\)
\(f'(x) =0\) とすると \(x = -1, 1\)
\(f^{\prime\prime}(-1)=6>0\)、 \(f^{\prime\prime}(1)=-6<0\) であるから
極小値は \(f(-1)=-2\)、極大値は \(f(1)=2\)
簡単に説明するよ
第2次導関数から極値を求める方法は
\(f'(x)=0\) になる \(x\) を求めて 、\(f^{\prime\prime}(x)\) に代入し、その値が \(+\) なら極小値、 \(-\) なら極大値
です。
メモメモ•••
詳しく説明するよ
第2次導関数から極値を求める方法を説明していきます。
極値って増減表を書けば分かるんだよね？
今回は増減表を書かずに求めていくよ。
そもそも極値とは「関数の増減が変わる場所」のことでした。
また、関数が増加するときは \(f'(x)\) は \(+\) であり、関数が減少するときは \(f'(x)\) は \(-\) でした。
そこで、\(f'(x)\) の \(+\) \(-\) が変わる可能性のある、\(f'(x)\) が \(0\) になる場所を考えます。
次の例題を使って説明していくよ！
関数 \(f(x)=-x^3+3x\) の極値を、第２次導関数を利用して求めよ。
関数 \(f(x)=-x^3+3x\) の増減は \(f'(x)=-3x^2+3\) が \(0\) になる場所で変わる可能性があります。
\(f'(x)=0\) とすると \(x = -1, 1\)
しかし、その場所が「極大」なのか「極小」なのか、それとも「極値をとらない」のかはまだ分かりません。
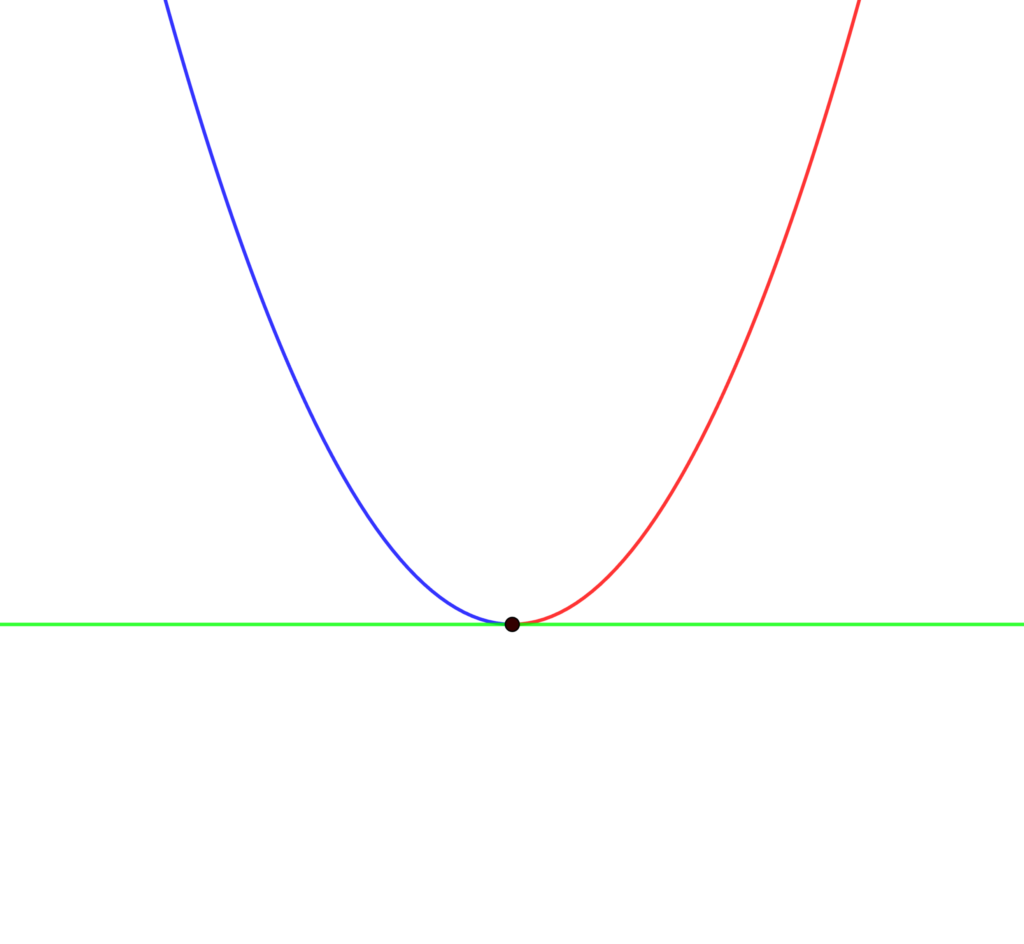
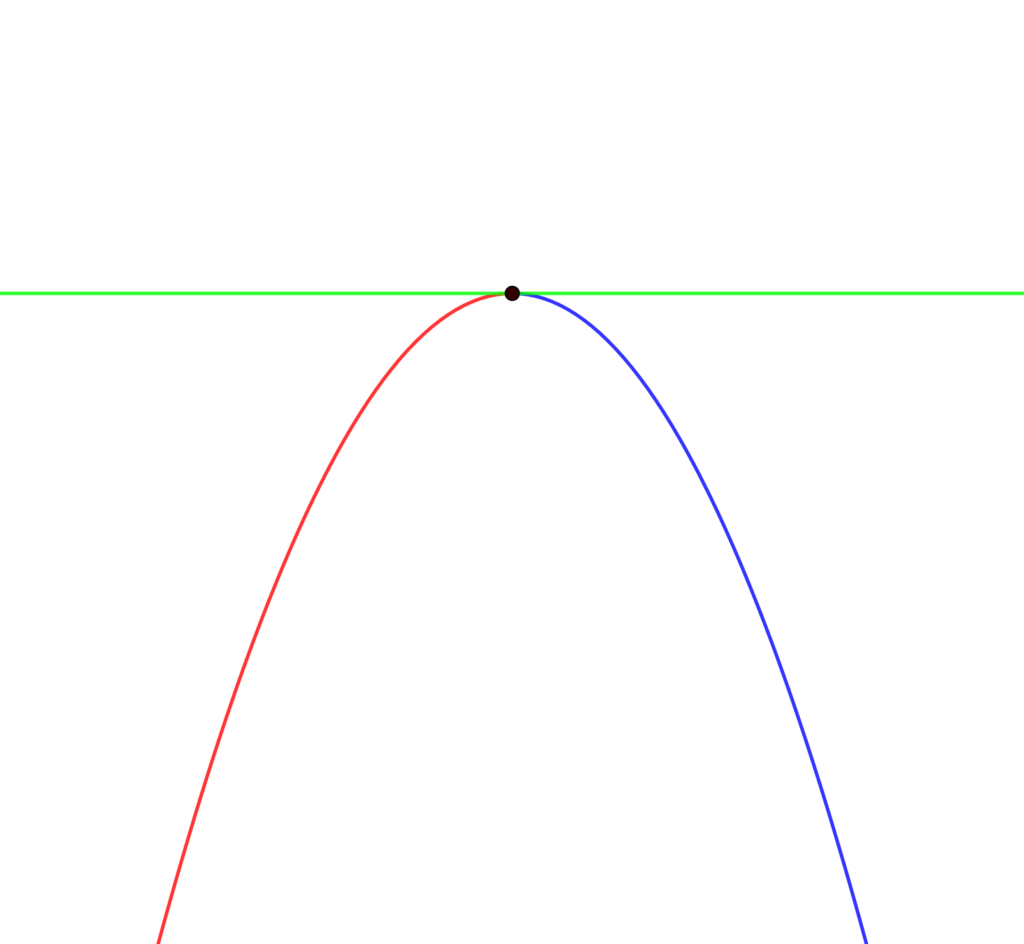
グラフは次の４通りが存在します。
極小
極大
極値をとらない
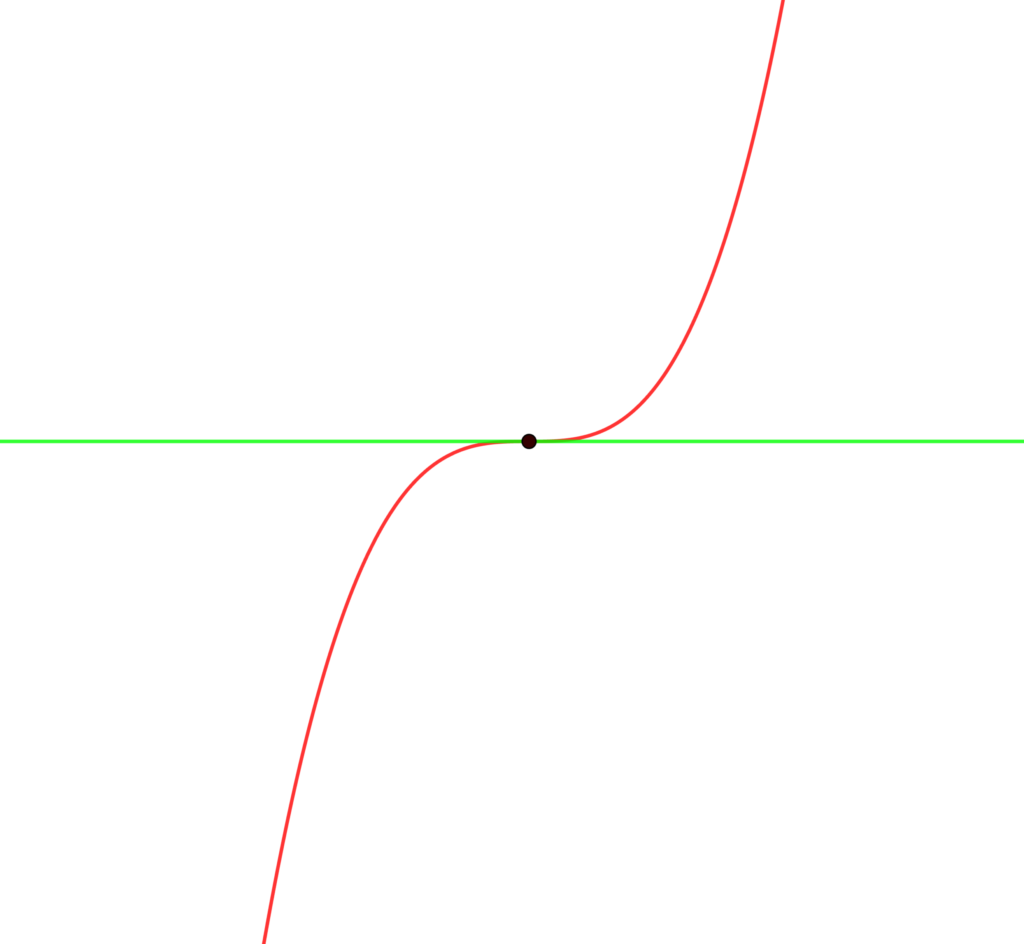
極値をとらない
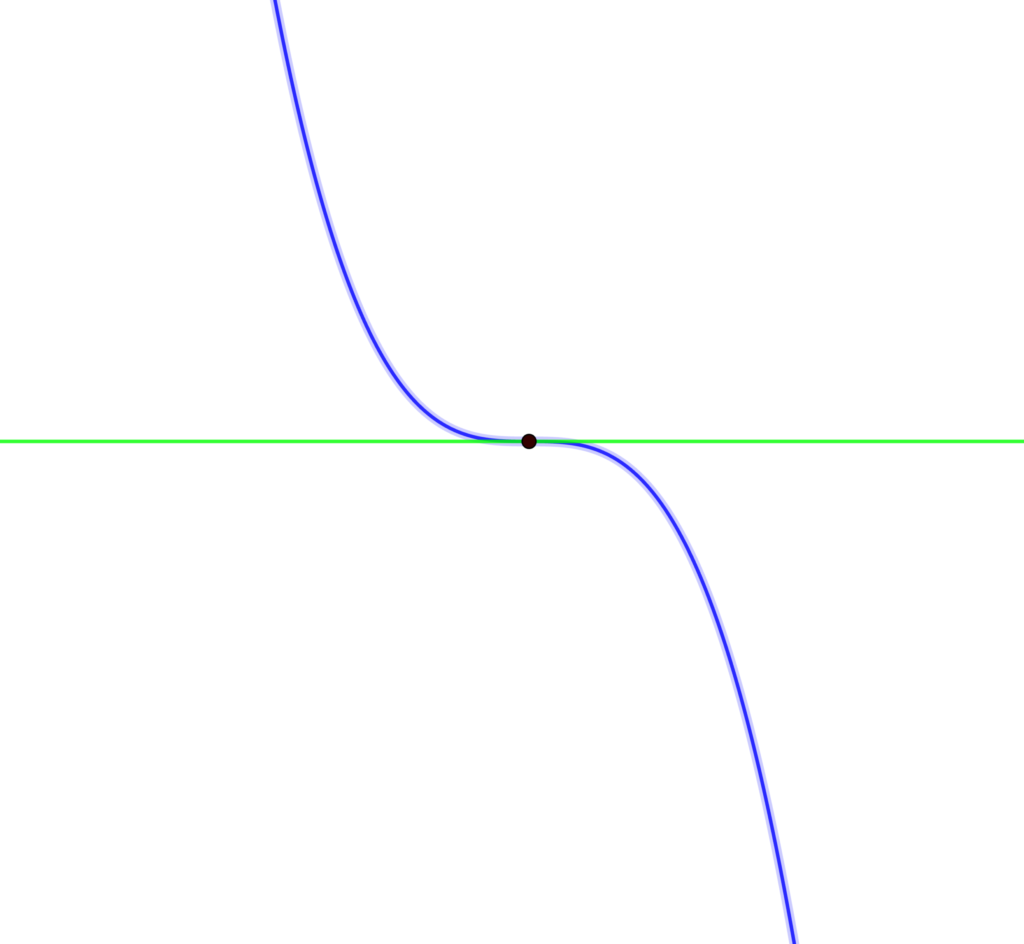
\(f'(x)=0\) でも極値をとるとは限らないんだね。
ここで「第2次導関数 \(f^{\prime\prime}(x)\) 」の出番ってわけ！
「第１次導関数 \(f^{\prime}(x)\) の\(+\) \(-\) 」では関数の「増減を判断」することができました。
そして、「第2次導関数 \(f^{\prime\prime}(x)\) の\(+\) \(-\) 」では関数の「凹凸を判断」することができます。
- 第2次導関数 \(f^{\prime\prime}(x)\) が \(+\) のとき、「下に凸」
- 第2次導関数 \(f^{\prime\prime}(x)\) が \(-\) のとき、「上に凸」
これを使うことで、さっきの４通りから「極大・極小」を判断することができるようになります。
もう一度さっきの図を確認しましょう。
「下に凸」（\(f^{\prime\prime}(a)>0\)）であれば「極小」、「上に凸」であれば（\(f^{\prime\prime}(a)<0\)）であれば「極大」となっています。
\(f^{\prime\prime}(x)>0\)
→ 下に凸
→ 極小
\(f^{\prime\prime}(x)<0\)
→ 上に凸
→ 極大
極値をとらない
極値をとらない
- \(f'(a)=0\) かつ \(f^{\prime\prime}(a)>0\) ならば、\(f(x)\) は \(x=a\) で極小である。
- \(f'(a)=0\) かつ \(f^{\prime\prime}(a)<0\) ならば、\(f(x)\) は \(x=a\) で極大である。
\(f^{\prime\prime}(x)=-6x\)
\(f^{\prime\prime}(-1)=6>0\)、 \(f^{\prime\prime}(1)=-6<0\) であるから
極小値は \(f(-1)=-2\)、極大値は \(f(1)=2\)
\(f'(a)=0\) だけでは、極値かどうかは分からなかったけど、\(f^{\prime\prime}(x)\) の\(+\) \(-\) と組み合わせることで判断できるんだね。
その通り！これが、「第2次導関数から極値を求める方法」だよ！
関数 \(f(x)=-x^3+3x\) の極値を、第２次導関数を利用して求めよ。
\(f^{\prime\prime}(x)=-6x\)
\(f'(x)=0\) とすると \(x = -1, 1\)
\(f^{\prime\prime}(-1)=6>0\)、 \(f^{\prime\prime}(1)=-6<0\) であるから
極小値は \(f(-1)=-2\)、極大値は \(f(1)=2\)
まとめ
今回の内容をしっかり整理しておこう！
第2次導関数を使えば、わざわざ増減表を書く必要がないから簡単だね！
- 関数の極値を求めるには、\(f'(x)=0\) となる点を探すところからスタート。
- でも、\(f'(x)=0\) になるだけでは、その点が極大値か極小値か、または極値を持たないかまでは分からない。
- そこで登場するのが 第2次導関数 \(f^{\prime\prime}(x)\) 。
- \(f^{\prime\prime}(x)>0\) → \(x=a\) で 極小
- \(f^{\prime\prime}(x)<0\) → \(x=a\) で 極大
- 「\(f'(x)=0\) ＋ 第2次導関数の符号判定」で、極値の種類をスピーディーに判断できる。
最初に戻って、教科書の説明を読んでみよう！スラスラ理解できるはずだよ！
コメント