
今日の板書はこれ!
\(\displaystyle\frac{a}{\sin{A}}=\frac{b}{\sin{B}}=\frac{c}{\sin{C}}=2R\)
(1) 1辺の長さが10の正三角形ABCの外接円の半径Rを求めよ。
(1) 正弦定理より
\(\displaystyle\frac{10}{\sin{60°}}\) \(=\) \(\displaystyle 2R\)
よって
\(\displaystyle R=\frac{10}{\frac{\sqrt{3}}{2}\cdot2}=\frac{10}{\sqrt{3}}=\frac{10\sqrt{3}}{2}\)
(2) △ABCにおいて、\(b=\sqrt{6}\) 、\(A=45°\)、\(B=60°\) のとき、\(a\) を求めよ。
(2) 正弦定理より
\(\displaystyle\frac{a}{\sin{45°}}\) \(=\) \(\displaystyle \frac{\sqrt{6}}{\sin{60°}}\)
よって
\(\displaystyle a=\frac{\sqrt{6}}{\frac{\sqrt{3}}{2}}\cdot\frac{1}{\sqrt{2}}=\frac{2\sqrt{6}}{\sqrt{3}}\cdot\frac{1}{\sqrt{2}}=2\)

もっと詳しく願いします!!
「人より勉強に時間がかかる」と感じていませんか?
私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。
• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」
• 「解答の意味が理解できず、勉強が進まない」
教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。
でも大丈夫!
このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。
「噛み砕き方」がわかれば、文章はぐっと読みやすくなります!
正弦定理
正弦定理とは?

正弦定理って何?

正弦定理は、「角(\(\sin\))」と「対辺」と「外接円の半径 」の関係式だよ!
\(\displaystyle\color{red}{\frac{a}{\sin{A}}}=\color{blue}{\frac{b}{\sin{B}}}=
\color{lime}{\frac{c}{\sin{C}}}=2\color{hotpink}{R}\)
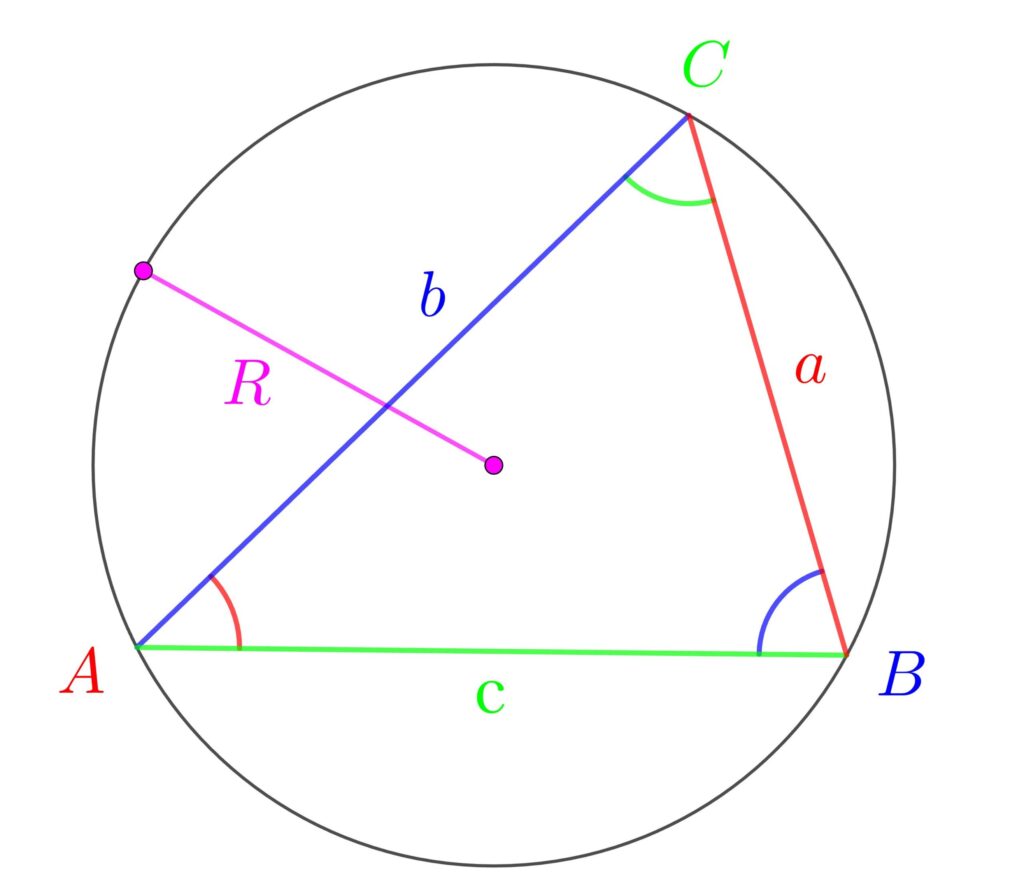
この式を言語化すると、「角(\(\sin\))と対辺の比はみんな同じ。外接円の直径と同じ。」です!
例題で使い方を覚えよう!

正弦定理は具体的にどうやって使うの?

例題で使い方を覚えよう!
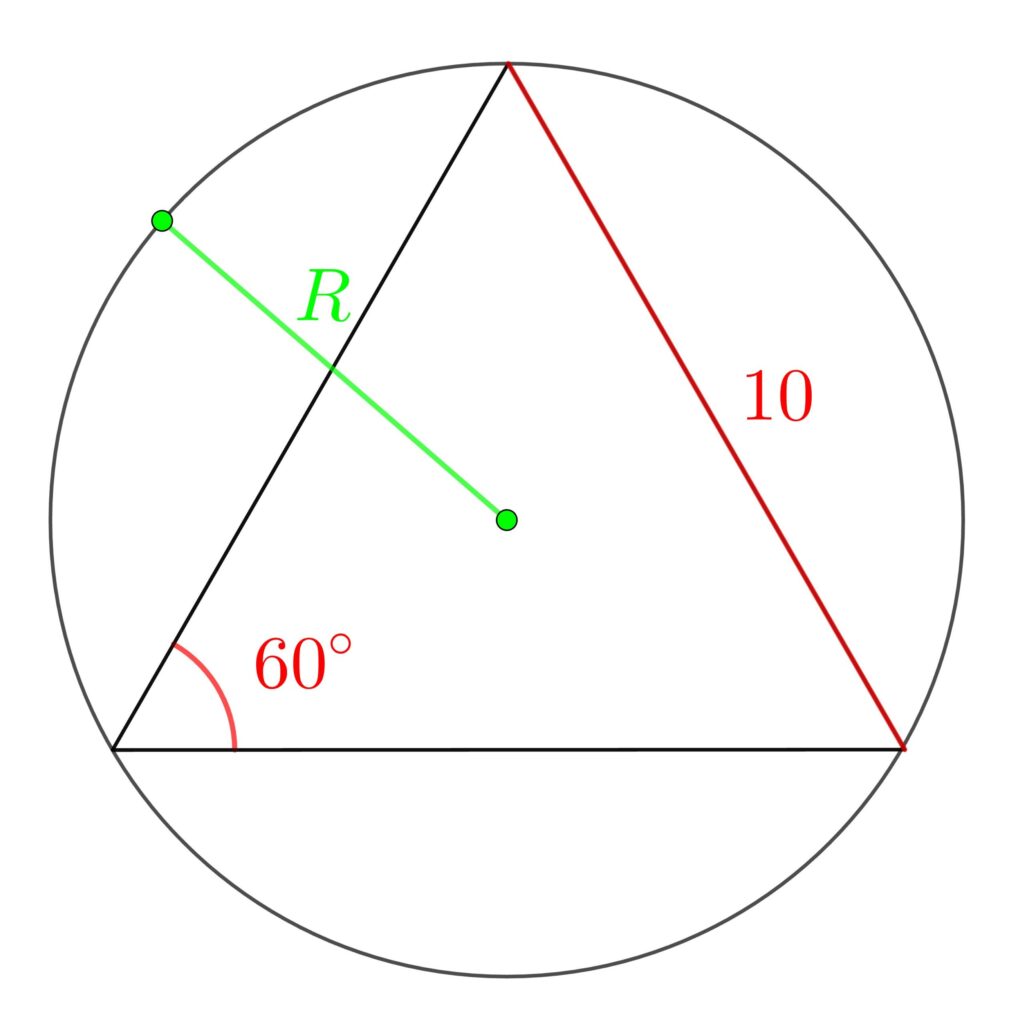
1辺の長さが10の正三角形ABCの外接円の半径Rを求めよ。
図で表すとこんな感じ!

正弦定理は、「角(\(\sin\))」と「対辺」と「外接円の半径 」の関係式です。
「角(\(\sin\))」と「対辺」が分かれば、「外接円の半径 」を求めることができます。
\(\displaystyle\frac{10}{\sin{60°}}\) \(=\) \(\displaystyle 2R\)
これを計算すると、
\(\displaystyle R=\frac{10}{\frac{\sqrt{3}}{2}\cdot2}=\frac{10}{\sqrt{3}}=\frac{10\sqrt{3}}{2}\)
正弦定理は、図で視覚的に覚えるのがオススメです。
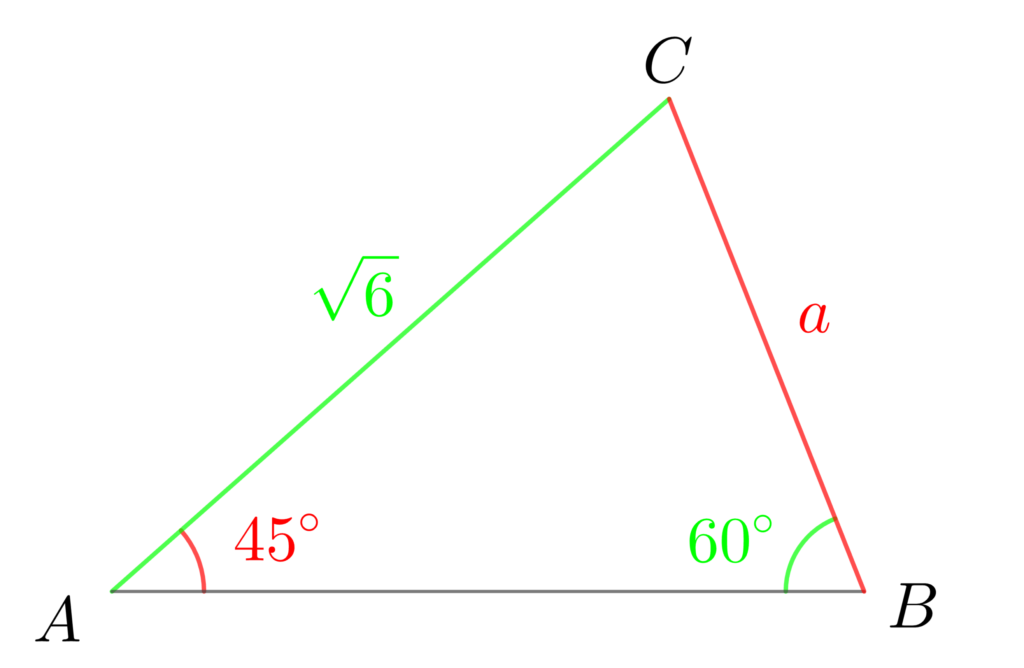
ではもう1問。
△ABCにおいて、\(b=\sqrt{6}\) 、\(A=45°\)、\(B=60°\) のとき、\(a\) を求めよ。
図で表すとこんな感じ!

正弦定理の式を言語化すると「角(\(\sin\))と対辺の比はみんな同じ。」でしたね。
緑のペアが揃っている状態で、赤の対辺を求めていきます。
\(\displaystyle\frac{a}{\sin{45°}}\) \(=\) \(\displaystyle \frac{\sqrt{6}}{\sin{60°}}\)
これを計算すると、
\(\displaystyle a=\frac{\sqrt{6}}{\frac{\sqrt{3}}{2}}\cdot\frac{1}{\sqrt{2}}=\frac{2\sqrt{6}}{\sqrt{3}}\cdot\frac{1}{\sqrt{2}}=2\)

角(\(\sin\))と対辺のペアを使うのが正弦定理なんだね!

視覚的に覚えたら、いつ正弦定理を使えばいいかが分かりやすいね!
正弦定理が成り立つ理由

そういえば、なんで正弦定理に外接円の半径が関わってくるの?

いい質問だね!正弦定理を導出してみようか。
次の三角形と外接円で考えていきましょう。
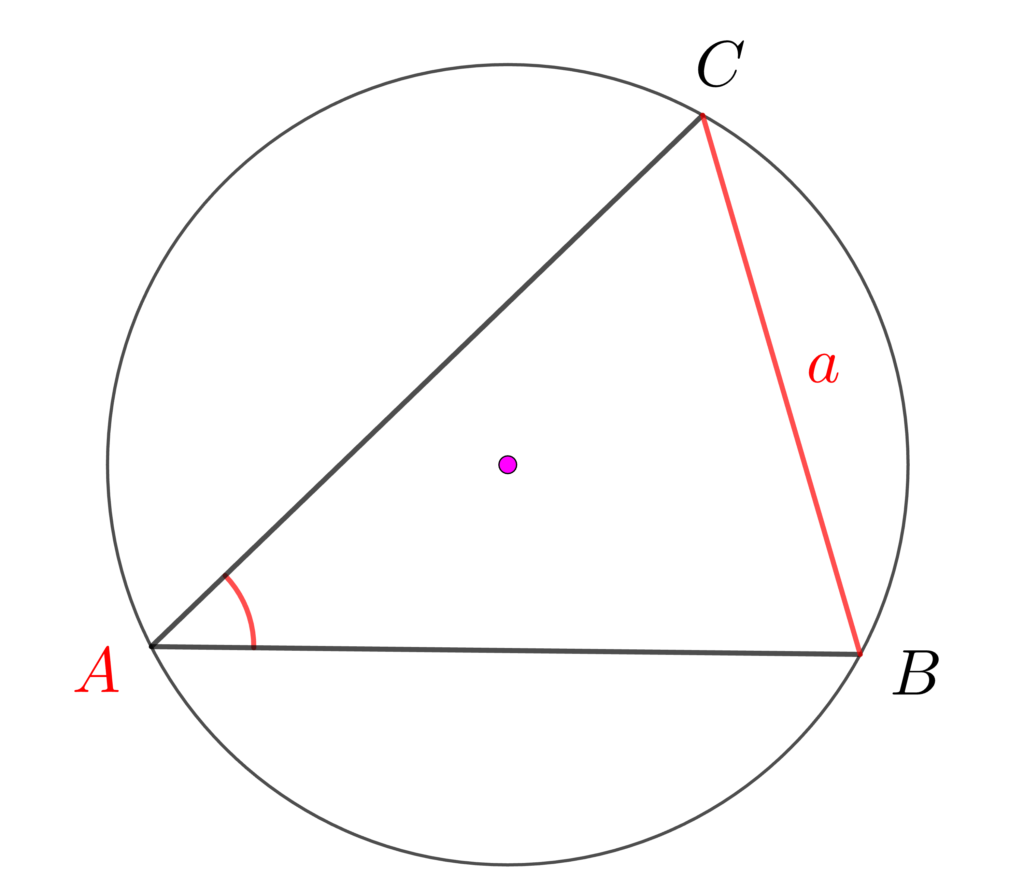
この三角形の頂点Aを少し動かします。
円周角の定理で、Aの角度を保ったまま移動ができます。
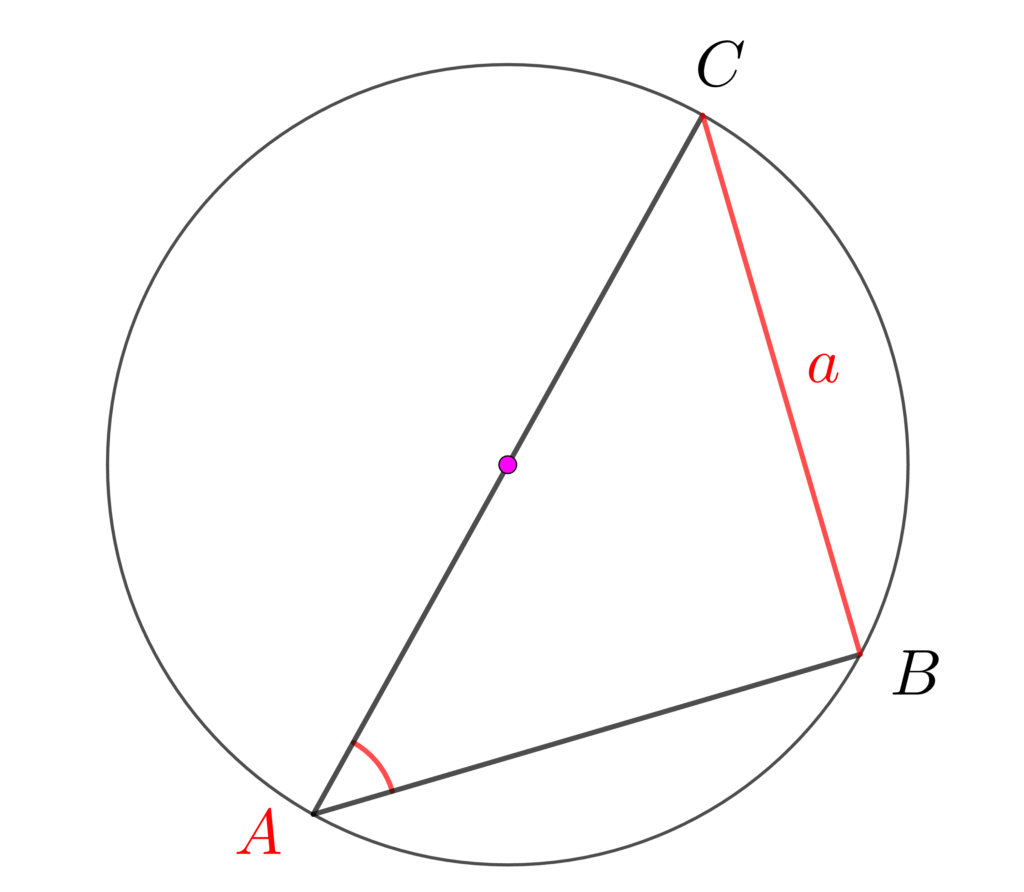
外接円の中心が辺に重なるように移動すると、線分ACが外接円の直径(半径×2)になり、角Bが90°になります。
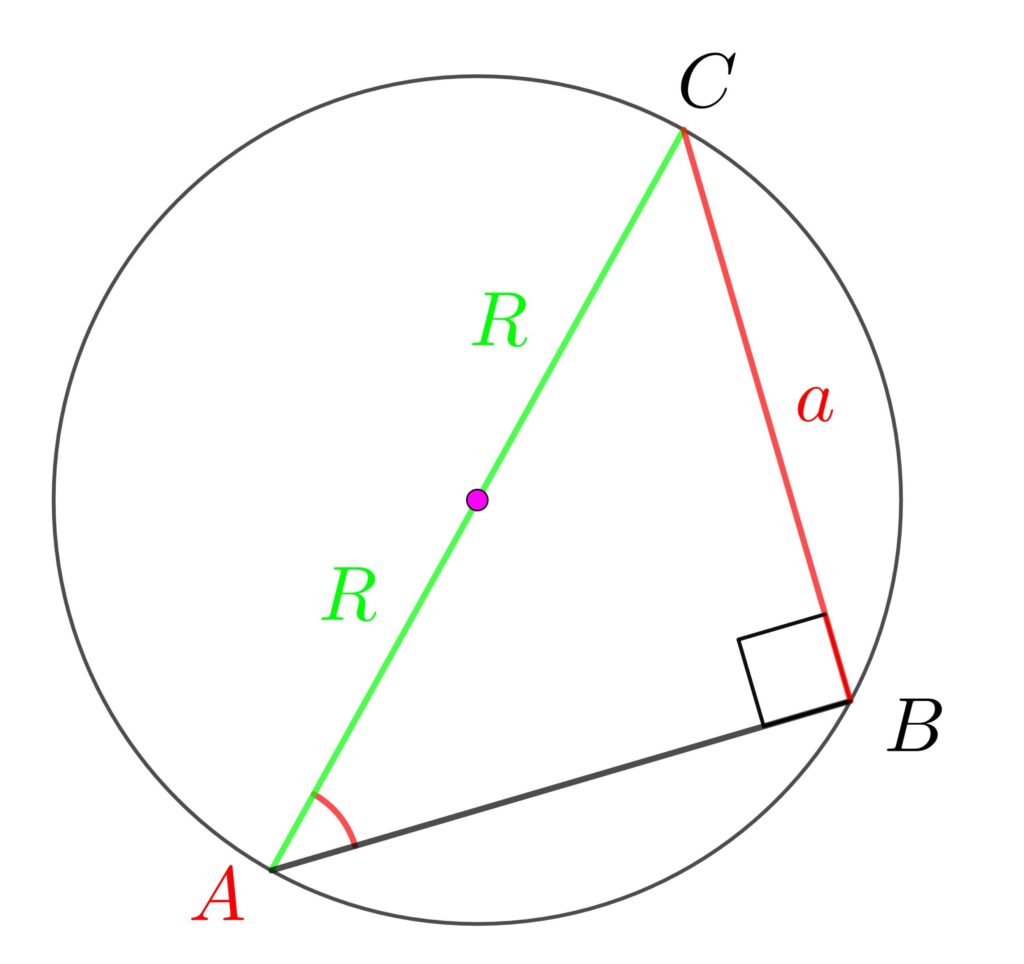
この直角三角形で、直角三角形の \(\sin\) の式を作ります。
\(\displaystyle\color{red}{\sin{A}}=\frac{\color{red}{a}}{\color{lime}{2R}}\)
式変形をして、
\(\displaystyle\frac{\color{red}{a}}{\color{red}{\sin{A}}}=\color{lime}{2R}\)
これで、「角(\(\sin\))」と「対辺」と「外接円の半径 」の関係式が立式できました。
あとは、角B、角Cで同じことをすると、正弦定理が完成します。
\(\displaystyle\frac{a}{\sin{A}}=\frac{b}{\sin{B}}=\frac{c}{\sin{C}}=2R\)
まとめ:正弦定理

さて、今回のまとめだよ!
正弦定理について勉強しました。
\(\displaystyle\frac{a}{\sin{A}}=\frac{b}{\sin{B}}=\frac{c}{\sin{C}}=2R\)
(1) 1辺の長さが10の正三角形ABCの外接円の半径Rを求めよ。
(1) 正弦定理より
\(\displaystyle\frac{10}{\sin{60°}}\) \(=\) \(\displaystyle 2R\)
よって
\(\displaystyle R=\frac{10}{\frac{\sqrt{3}}{2}\cdot2}=\frac{10}{\sqrt{3}}=\frac{10\sqrt{3}}{2}\)

(2) △ABCにおいて、\(b=\sqrt{6}\) 、\(A=45°\)、\(B=60°\) のとき、\(a\) を求めよ。
(2) 正弦定理より
\(\displaystyle\frac{a}{\sin{45°}}\) \(=\) \(\displaystyle \frac{\sqrt{6}}{\sin{60°}}\)
よって
\(\displaystyle a=\frac{\sqrt{6}}{\frac{\sqrt{3}}{2}}\cdot\frac{1}{\sqrt{2}}=\frac{2\sqrt{6}}{\sqrt{3}}\cdot\frac{1}{\sqrt{2}}=2\)


また一つ賢くなった!






コメント