今日の板書はこれ！
単位時間あたりの位置の変化のこと。位置を微分すると速度になる。
単位時間あたりの速度の変化のこと。速度を微分すると加速度になる。
詳しく願いします！！
「人より勉強に時間がかかる」と感じていませんか？
私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。
• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」
• 「解答の意味が理解できず、勉強が進まない」
教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。
でも大丈夫！
このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。
「噛み砕き方」がわかれば、文章はぐっと読みやすくなります！
頑張っているのに、なかなか成績が上がらなくて、苦しんでる方へ。
画像をクリックして、記事を読んでみて。
きっと力になるはず。
速度とは
単位時間あたりの位置の変化のこと。位置を微分すると速度になる。
簡単にいうと、車のスピードメーターのこと！
時速60kmとかのやつか。でも、単位時間ってなに？
単位時間あたりの位置の変化
単位時間とは、「1秒」とか「１時間」とかの、時間の「１単位」のことです。
例えば、
単位が「秒」であれば、1秒間あたりに移動する速度を「秒速」
単位が「時間」であれば、1時間あたりに移動する速度を「時速」
といいます。
時速60kmは、「１時間あたり60km進む」ってことか。
そういうこと！
位置を微分すると速度になる
じゃあ「位置を微分すると速度になる」ってどういうこと？
具体例として、点Pを使って説明するね！点Pは車だって思えば、イメージしやすいよ。
次の例題を考えていきましょう。
数直線上を動く点Pの座標が、時刻 \(t\) の関数として、 \(x = -t^3+3t^2\) と表されるとき、時刻 \(t\) における点Pの速度 \(v\) 、加速度 \(\alpha\) を求めよ。
まずは、点Pの時刻 \(t\) に対する位置から考えてみるよ！
時刻 \(t=0\) のとき、点Pの位置は
\(x=-0^3+3\cdot0^2=0\)
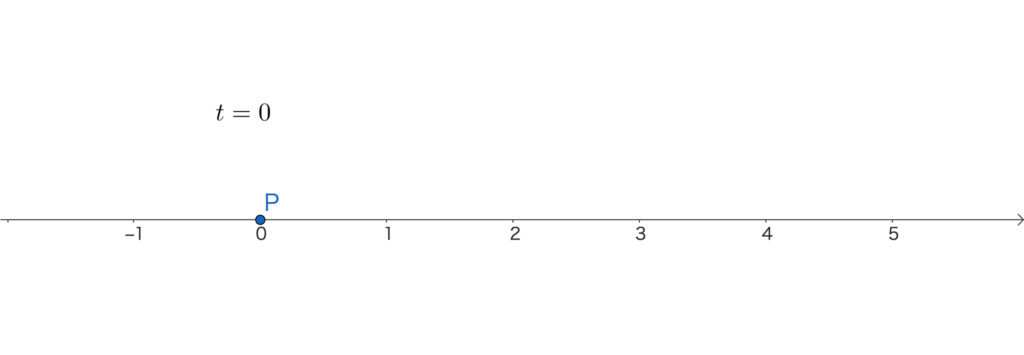
時刻 \(t=1\) のとき、点Pの位置は
\(x=-1^3+3\cdot1^2=2\)
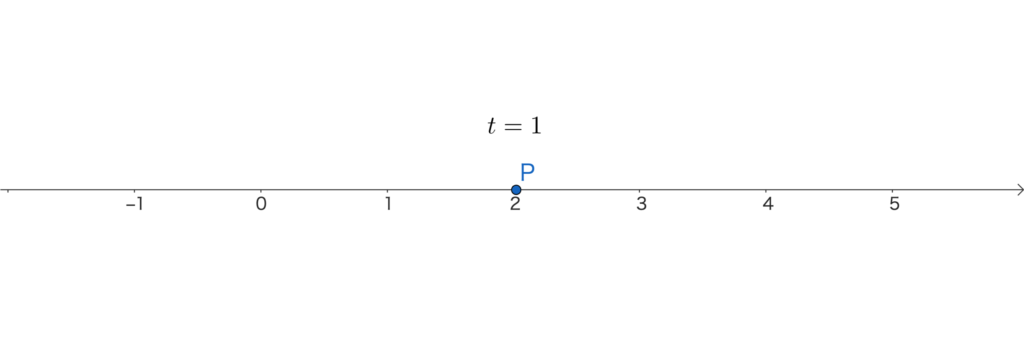
時刻 \(t=2\) のとき、点Pの位置は
\(x=-2^3+3\cdot2^2=4\)
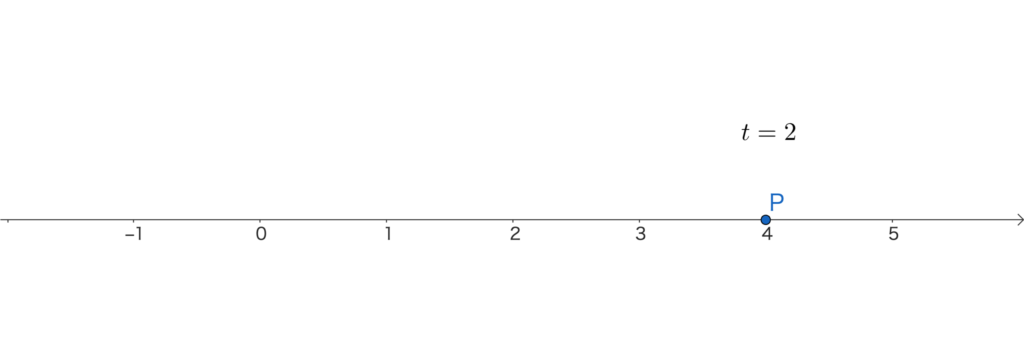
時刻 \(t=3\) のとき、点Pの位置は
\(x=-3^3+3\cdot3^2=0\)
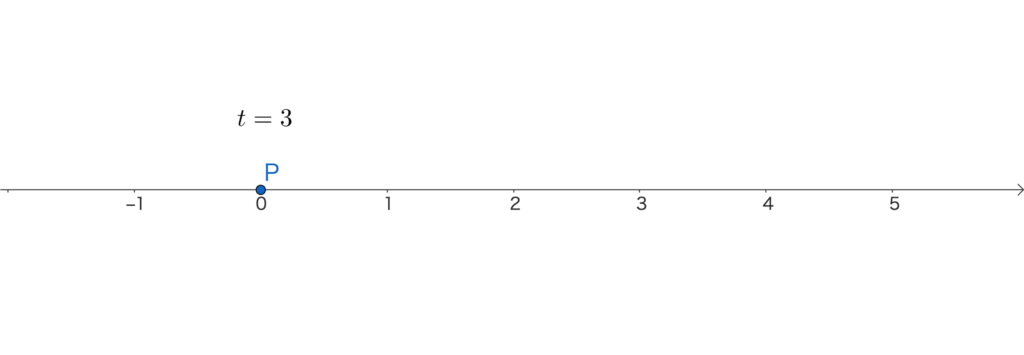
ちょっと進んで、ぐっと戻ってるね。
この点Pの速度は微分したら求めることができるんだ！
位置の関数 \(x = -t^3+3t^2\) を微分します。
\(v=\frac{dx}{dt} = -3t^2+6t\)
これが、点Pの速度の関数になります。
つまり、
時刻 \(t=0\) のとき、点Pの速度は
\(v=\frac{dx}{dt}=-3\cdot0^2+6\cdot0=0\)
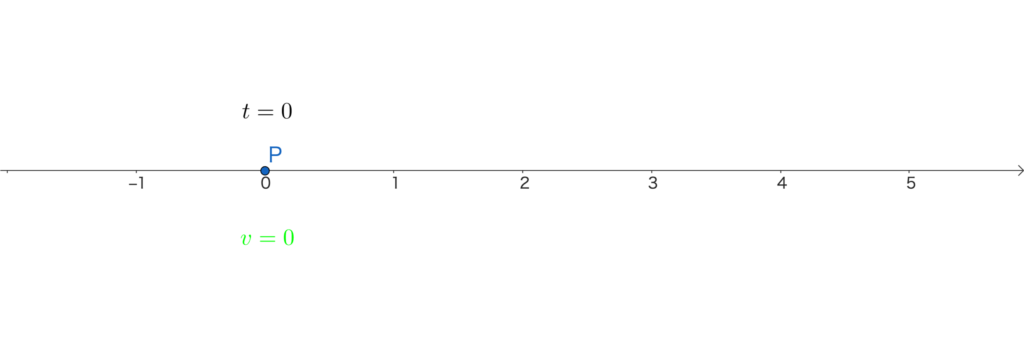
時刻 \(t=1\) のとき、点Pの速度は
\(v=\frac{dx}{dt}=-3\cdot1^2+6\cdot1=3\)
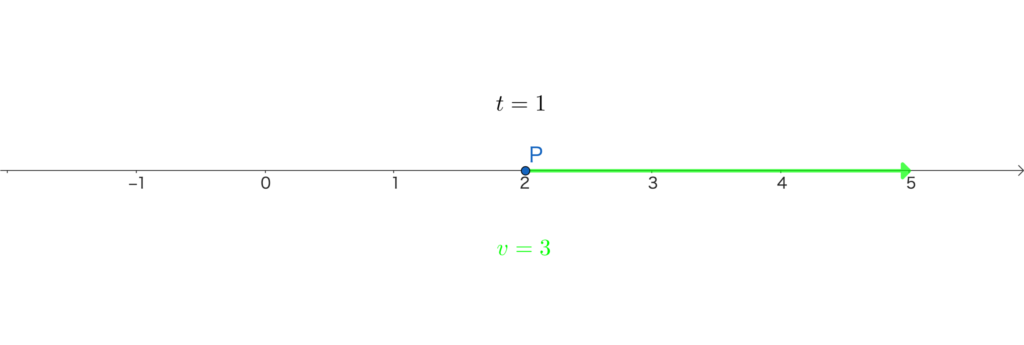
時刻 \(t=2\) のとき、点Pの速度は
\(v=\frac{dx}{dt}=-3\cdot2^2+6\cdot2=0\)
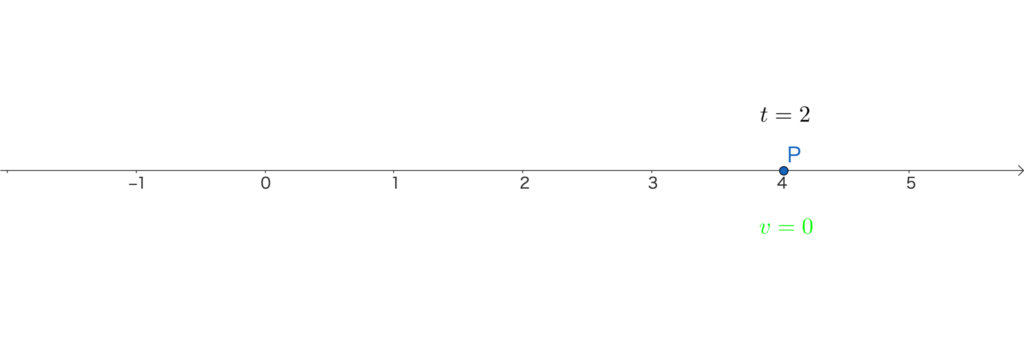
時刻 \(t=3\) のとき、点Pの速度は
\(v=\frac{dx}{dt}=-3\cdot3^2+6\cdot3=-9\)
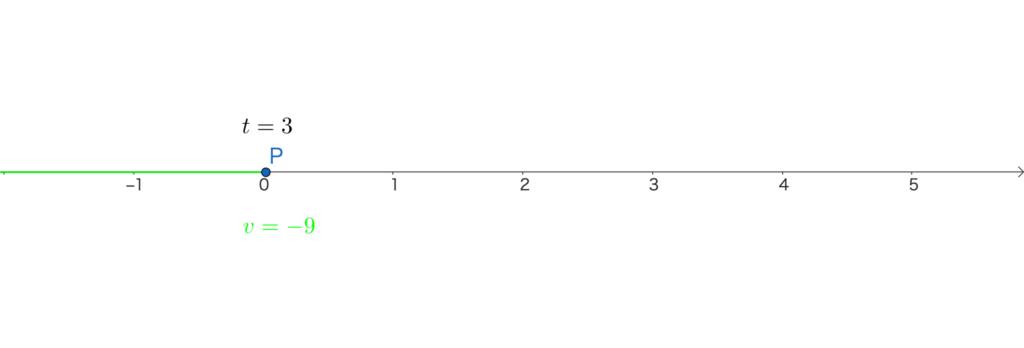
点Pは、\(t=0\) からだんだん加速していき、\(t=2\) までに、だんだん減速していきます。
\(t=2\) で一旦速度が、\(0\) になった後、反対方向に一気に加速していきます。
車のスピードメーターってイメージだとわかりやすいね。
車にマイナスの速度はないけど、イメージの話！許してね！
理由
なんで位置を微分したら速度になるの？
\(t=1\) のときの速度を例に丁寧に考えていくね。
点Pの位置の関数を
\(f(t)=-t^3+3t^2\)
とします。
速度は常に変化しますので、とりあえず、\(t=1\) から \(t=2\) までの平均速度を考えましょう。
速度は、単位時間の変化量なので、
\(\frac{f(2)-f(1)}{2-1}=\frac{(-2^3+3\cdot2^2)-(-1^3+3\cdot1^2)}{2-1}=2\)
となります。
これが理解できたら次に、\(t=1\) の瞬間の速度を考えます。
瞬間の速度は、\(t=1\) から \(t=1+\Delta t\) までの平均速度に対して、\(\Delta t → 0\) とすることで求めることができます。
\(\Delta t\)は「ちょっとの時間」って意味だよ！
\(t=1\) から \(t=1+\Delta t\) までの平均速度は、
\(\frac{f(1+\Delta t)-f(1)}{\Delta t}\)
瞬間の速度にするために、\(\Delta t → 0\) とすると、
\(\displaystyle\lim_{\Delta t \to 0} \frac{f(1+\Delta t)-f(1)}{\Delta t}\)
あ！この式って微分の定義だ！
その通り！ある瞬間の速度が知りたかったら、位置を微分しよう！
加速度とは
単位時間あたりの速度の変化のこと。速度を微分すると加速度になる。
加速度って何？
単位時間あたりの速度の変化量のこと
加速度とは、「単位時間あたりの速度の変化量のこと」です。
例えば、加速度は30km/h\(^2\) とは、1時間ごとに時速が30kmずつ増えるということです。
今が、時速30kmであれば、１時間後には時速60kmに、２時間後には時速90kmのペースで加速していきます。
速度を微分すると加速度になる
加速度は、速度を微分したものなの？
その通り！車のアクセルをイメージしてみて。
数直線上を動く点Pの座標が、時刻 \(t\) の関数として、 \(x = -t^3+3t^2\) と表されるとき、時刻 \(t\) における点Pの速度 \(v\) 、加速度 \(\alpha\) を求めよ。
点Pの速度 \(v\) は \(v=\frac{dx}{dt} = -3t^2+6t\) でした。
点Pの加速度 \(\alpha\) は
\(\alpha=\frac{dv}{dt}= -6t+6\)
となります。
時刻 \(t=0\) のとき、点Pの加速度は
\(\alpha=\frac{dv}{dt}=-6\cdot0+6=6\)
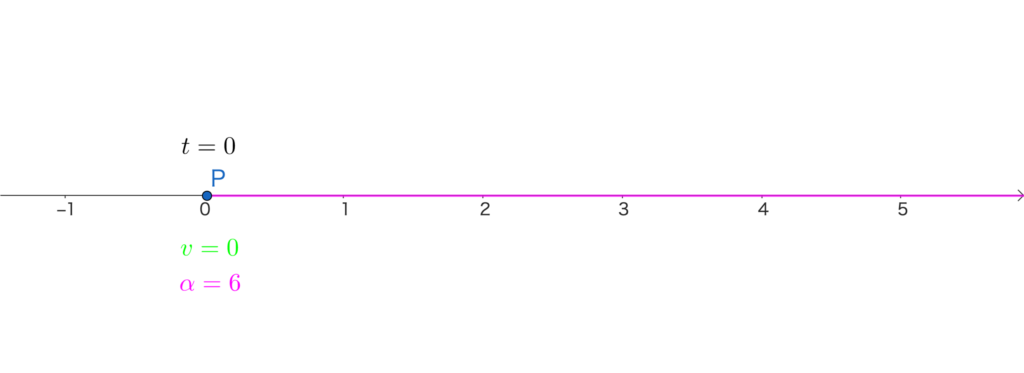
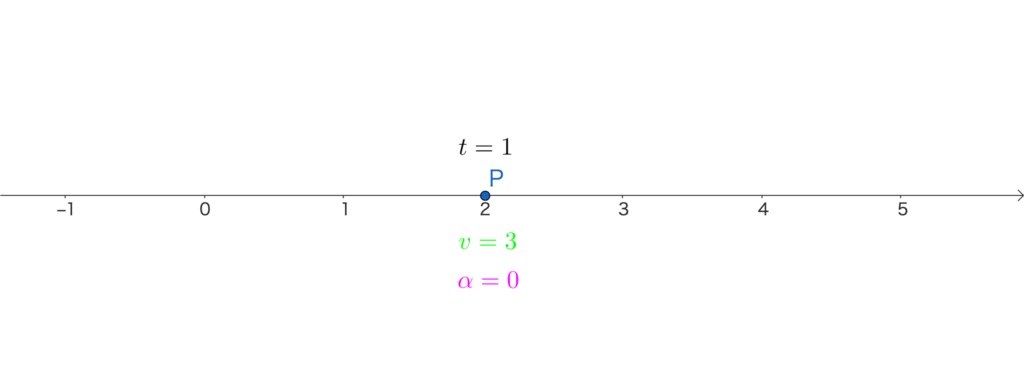
時刻 \(t=1\) のとき、点Pの加速度は
\(\alpha=\frac{dv}{dt}=-6\cdot1+6=0\)
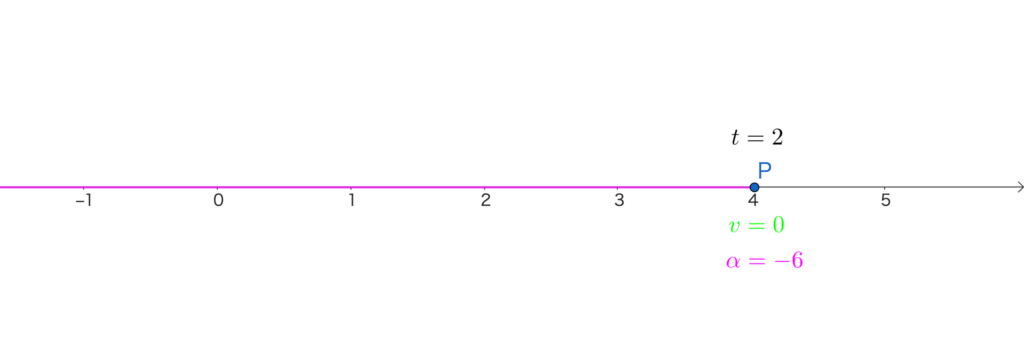
時刻 \(t=2\) のとき、点Pの加速度は
\(\alpha=\frac{dv}{dt}=-6\cdot2+6=-6\)
時刻 \(t=3\) のとき、点Pの加速度は
\(\alpha=\frac{dv}{dt}=-6\cdot3+6=-12\)
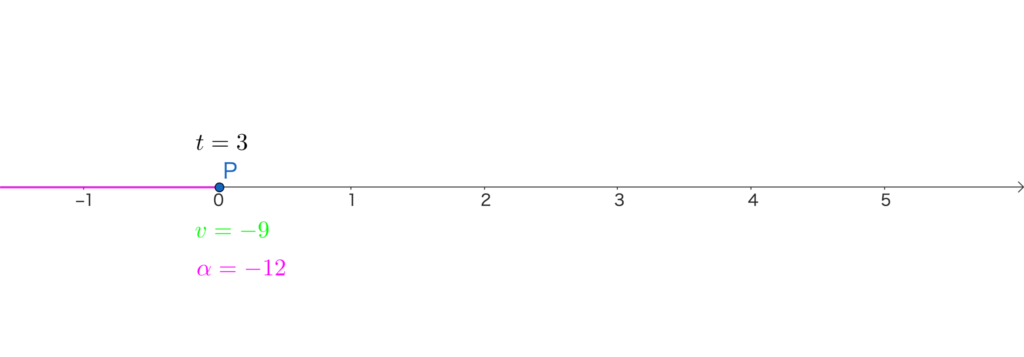
点Pは、\(t=0\) からアクセルを踏み始め、だんだん弱めていきます。
\(t=1\) で一旦アクセルから足を離し、その後反対方向にペダルを踏み込みんでいます。
速度はスピードメーター、加速度はアクセルって考えるとわかりやすい！
理由
速度を微分する加速度になる理由もさっきと一緒？
お。よくわかったね。
加速度は、単位時間あたりの速度の変化ですから、
となります。
まとめ
さて、今回のまとめだよ！
単位時間あたりの位置の変化のこと。位置を微分すると速度になる。
単位時間あたりの速度の変化のこと。速度を微分すると加速度になる。
数直線上を動く点Pの座標が、時刻 \(t\) の関数として、 \(x = -t^3+3t^2\) と表されるとき、時刻 \(t\) における点Pの速度 \(v\) 、加速度 \(\alpha\) を求めよ。
\(v=\frac{dx}{dt} = -3t^2+6t\)
\(\alpha=\frac{dv}{dt}= -6t+6\)
また一つ賢くなった！
頑張っているのに、なかなか成績が上がらなくて、苦しんでる方へ。
画像をクリックして、記事を読んでみて。
きっと力になるはず。
↑前の記事↑
↑次の記事↑
コメント