
今日の板書はこれ!
Aが鋭角 \( \Leftrightarrow \cos{A}>0 \Leftrightarrow \) \(b^2+c^2-a^2>0\)
Aが直角 \( \Leftrightarrow \cos{A}=0 \Leftrightarrow \) \(b^2+c^2-a^2=0\)
Aが鈍角 \( \Leftrightarrow \cos{A}<0 \Leftrightarrow \) \(b^2+c^2-a^2<0\)
3辺の長さが \(a=9\), \(b=3\sqrt{2}\), \(c=7\) である△ABCは鋭角三角形・直角三角形・鈍角三角形のどれであるか。
\((3\sqrt{2})\:^2+7\:^2-9\:^2=-14<0\) より △ABC は 鈍角三角形

もっと詳しく願いします!!
現役教員として数学を教えている「さん」と申します。
「人より勉強に時間がかかる」と感じていませんか?
私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。
• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」
• 「解答の意味が理解できず、勉強が進まない」
教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。
でも大丈夫!
このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。
意味から理解し、噛み砕き方をマスターしましょう!!
鋭角三角形・鈍角三角形・直角三角形の条件とは?

三角形が鋭角・直角・鈍角のどれかってどうやって判断するの?

一番大きい角の大きさで判断するんだよ!
三角形の一番大きい角が、
90°未満であれば鋭角三角形、90°であれば直角三角形、90°以上であれば鈍角三角形です。

じゃあ、角度を見れば判断できるんだね!

次の例題の三角形ではどうかな?
3辺の長さが \(a=9\), \(b=3\sqrt{2}\), \(c=7\) である△ABCは鋭角三角形・直角三角形・鈍角三角形のどれであるか。
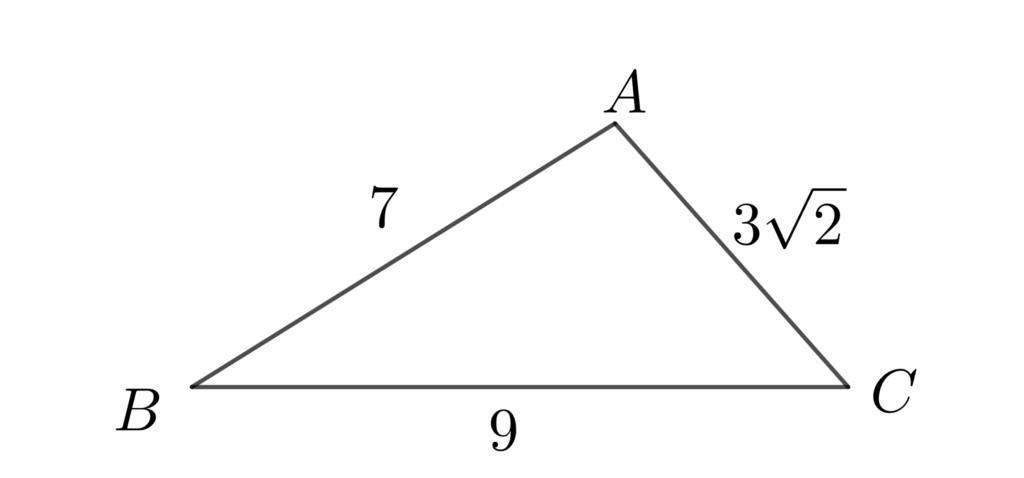

角度が1つも分からない•••

こんなときは、次の公式を使おう!
三角形の角の大小は、辺の大小と一致するので、一番大きい 辺a に対する 角A について考えます。
\(b^2+c^2-a^2>0 \Leftrightarrow \) Aが鋭角
\(b^2+c^2-a^2=0 \Leftrightarrow \) Aが直角
\(b^2+c^2-a^2<0 \Leftrightarrow \) Aが鈍角
\(b^2+c^2-a^2\) の「 + , 0 , – 」で、Aの「鋭角・直角・鈍角」を判断していきます。
\((3\sqrt{2})\:^2+7\:^2-9\:^2=-14<0\) より △ABC は 鈍角三角形
公式の意味を解説!

え、なんでこれで判断できるの?

分かりやすく解説していくね!
角度が「90°未満・90°・90°以上」かが分かれば、「鋭角・直角・鈍角」を判断できます。
そして、3辺の長さから角度を求めるのは、余弦定理でした。
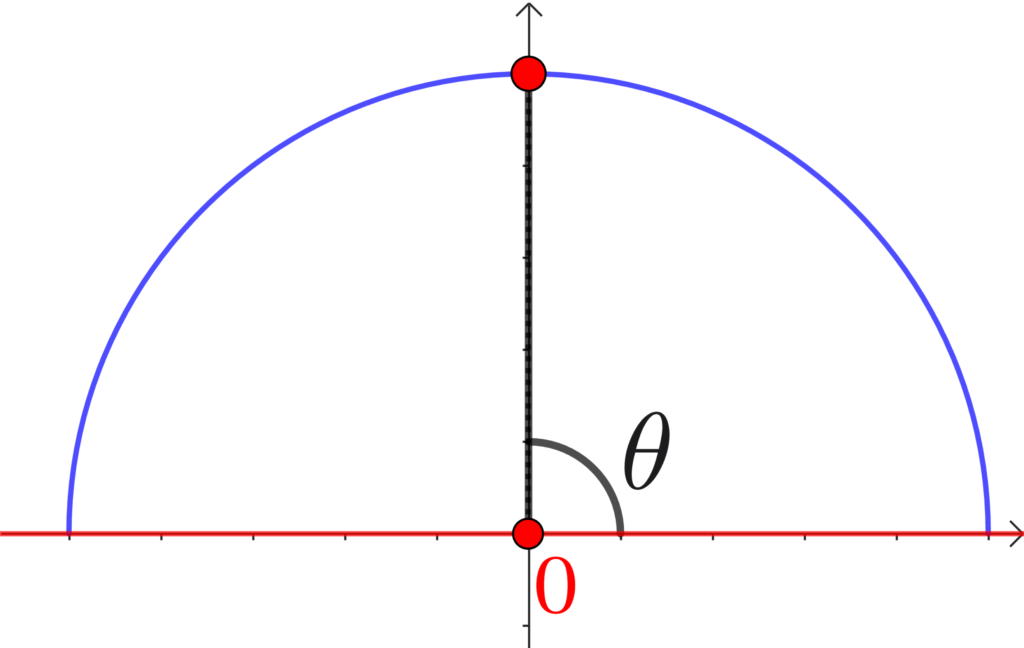
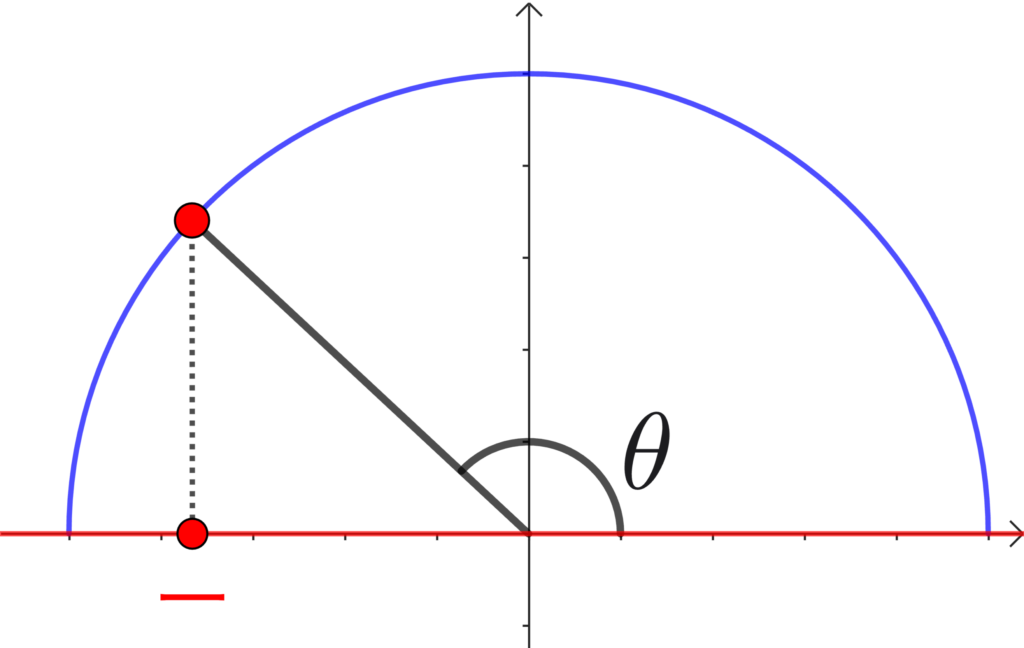
\(\cos\) は、「 + のとき 90°未満」「 0 のとき 90°」「 – のとき 90°以上」ですから、次が成り立ちます。
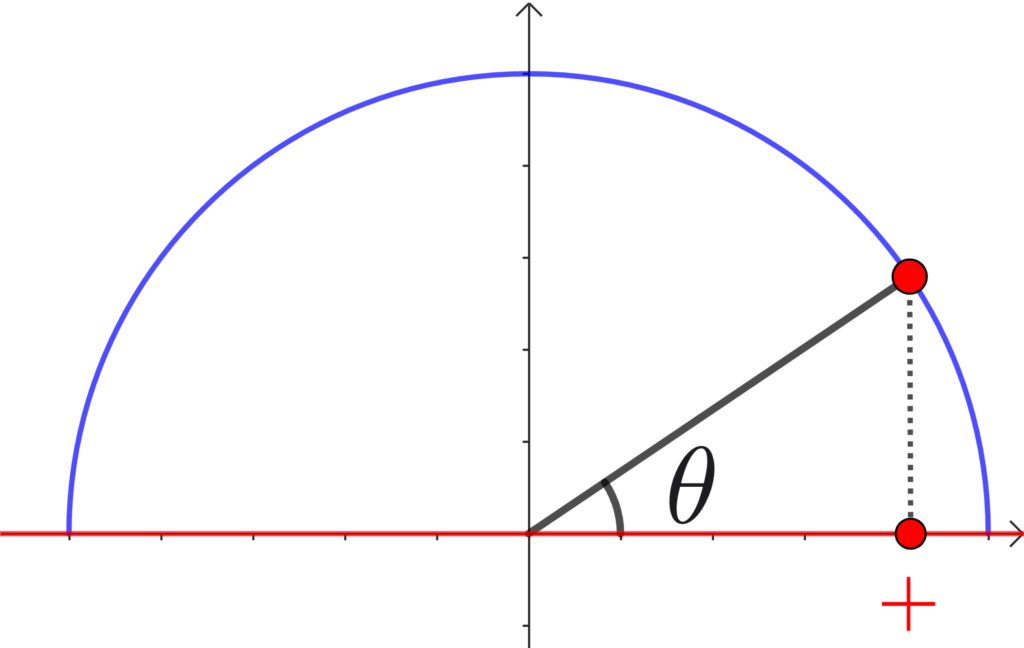
\(\cos{A}>0 \Leftrightarrow \displaystyle\frac{b^2+c^2-a^2}{2bc}>0 \Leftrightarrow \) Aが鋭角
\(\cos{A}=0 \Leftrightarrow \displaystyle\frac{b^2+c^2-a^2}{2bc}=0 \Leftrightarrow \) Aが直角
\(\cos{A}<0 \Leftrightarrow \displaystyle\frac{b^2+c^2-a^2}{2bc}<0 \Leftrightarrow \) Aが鈍角
さらに、\(\displaystyle\frac{b^2+c^2-a^2}{2bc}\) の 分母2bc は必ず + なので、分子\(b^2+c^2-a^2\) の「 + , 0 , – 」だけを判断すればOKです。
Aが鋭角 \( \Leftrightarrow \cos{A}>0 \Leftrightarrow \) \(b^2+c^2-a^2>0\)
Aが直角 \( \Leftrightarrow \cos{A}=0 \Leftrightarrow \) \(b^2+c^2-a^2=0\)
Aが鈍角 \( \Leftrightarrow \cos{A}<0 \Leftrightarrow \) \(b^2+c^2-a^2<0\)

なるほど!!余弦定理の分子の符号で判断してるのか!
まとめ:正弦定理の比例式

さて、今回のまとめだよ!
Aが鋭角 \( \Leftrightarrow \cos{A}>0 \Leftrightarrow \) \(b^2+c^2-a^2>0\)
Aが直角 \( \Leftrightarrow \cos{A}=0 \Leftrightarrow \) \(b^2+c^2-a^2=0\)
Aが鈍角 \( \Leftrightarrow \cos{A}<0 \Leftrightarrow \) \(b^2+c^2-a^2<0\)
3辺の長さが \(a=9\), \(b=3\sqrt{2}\), \(c=7\) である△ABCは鋭角三角形・直角三角形・鈍角三角形のどれであるか。
\((3\sqrt{2})\:^2+7\:^2-9\:^2=-14<0\) より △ABC は 鈍角三角形

また一つ賢くなった!






コメント