【意味から理解！】三角比による三角形の面積Sの求め方と公式の証明

さん

今日の板書はこれ！

三角比による三角形の面積

\(S=\frac{1}{2}bc\sin{A}\)

例題

\(A=60°\), \(b=4\), \(c=3\), である△ABCの面積Sを求めよ。

解答

\( \begin{aligned} \displaystyle S &= \frac{1}{2} \cdot 4 \cdot 3 \cdot \sin{60°} \\ \\ &= 3\sqrt{3} \\ \end{aligned} \)

生徒

もっと詳しく願いします！！

現役教員として数学を教えている「さん」と申します。

「人より勉強に時間がかかる」と感じていませんか？

私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。

• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」

• 「解答の意味が理解できず、勉強が進まない」

教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。

でも大丈夫！

このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。

意味から理解し、噛み砕き方をマスターしましょう！！

勉強しても成績が上がらない3つの理由と現役教師が教えるたった1つの解決策

一生懸命やってるのに結果が出ない…そんな中高生の悩みを、現役教師が本気で解決！信頼できる家庭教師が導く正しい学び方とは？

三角比による三角形の面積Sの求め方と公式の証明
1. 三角比による三角形の面積Sの求め方
2. 公式の証明
まとめ：三角比による三角形の面積

三角比による三角形の面積Sの求め方と公式の証明

さん

今回は２辺とその間の角から面積を求める方法を学ぼう！

生徒

（底辺）×（高さ）÷ 2 じゃなくても求めれるの？

三角比による三角形の面積Sの求め方

三角比による三角形の面積は次のように求めます。

三角比による三角形の面積

\(S=\frac{1}{2}bc\sin{A}\)

では実際に、次の例題で使ってみましょう。

例題

\(A=60°\), \(b=4\), \(c=3\), である△ABCの面積Sを求めよ。

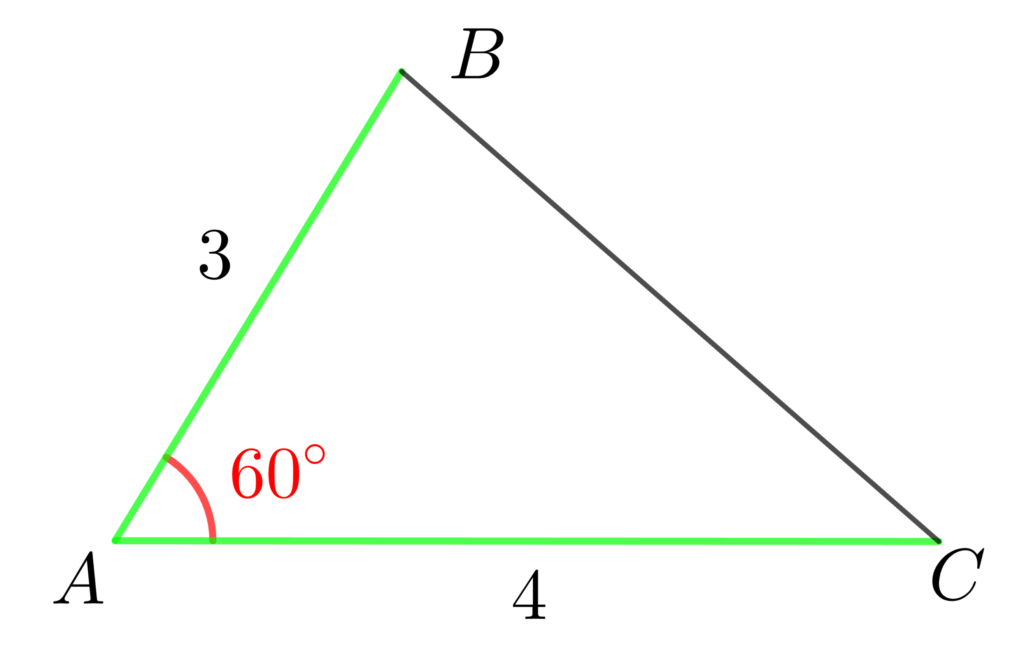
\(\displaystyle S=\frac{1}{2}\cdot\color{lime}{b}\cdot\color{lime}{c}\cdot\color{red}{\sin{A}}\) は２辺とその間の角が分かるときに使える公式です。

\( \begin{aligned} \displaystyle S &= \frac{1}{2} \cdot \color{lime}{4} \cdot \color{lime}{3} \cdot \color{red}{\sin{60°}} \\ \\ &= \frac{1}{2} \cdot 4 \cdot 3 \cdot \frac{\sqrt{3}}{2} \\ \\ &= 3\sqrt{3} \\ \end{aligned} \)

さん

三角形の面積は「２辺とその間が分かるとき」に求められるって覚えておこう！

公式の証明

生徒

なんでこの公式でも求められるの？

さん

それは「（底辺）×（高さ）÷ 2」を使っているからだよ！

例題

\(A=60°\), \(b=4\), \(c=3\), である△ABCの面積Sを求めよ。

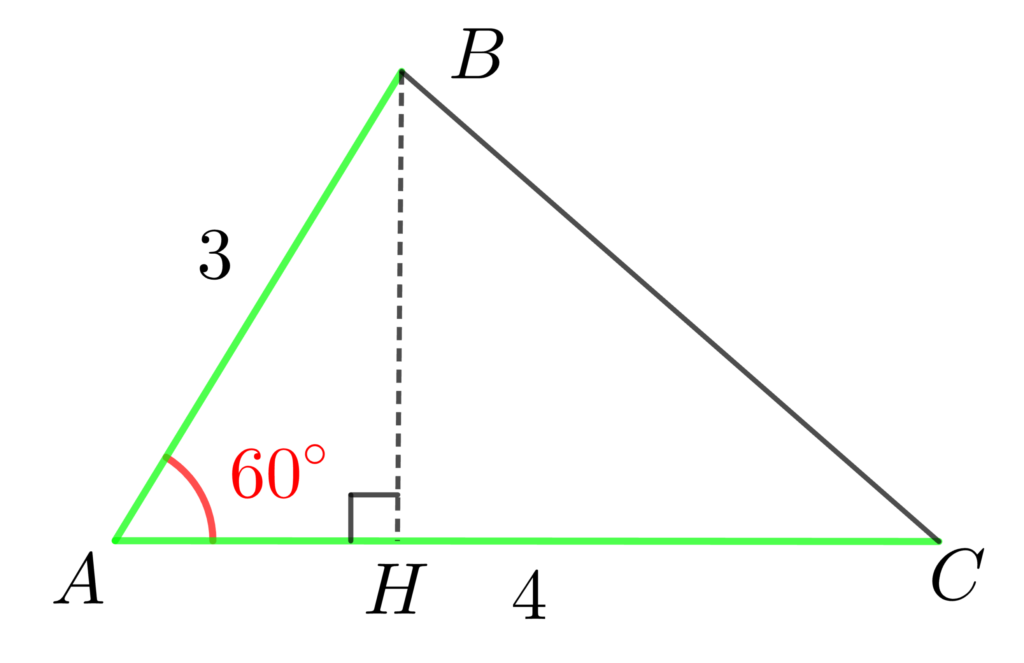
この例題では底辺\(AC\) の値は４だと与えられていますが、高さ\(BH\) の値が分かりません。

そこで△ABHの直角三角形を使って、高さ \(BH\) を求めていきます。

\(\displaystyle\sin{60°}=\frac{BH}{3}\) より

\(\displaystyle \color{hotpink}{BH=3\cdot\sin{60°}}\)

よって、「（底辺）×（高さ）÷ 2」を使うと下のようになります。

\( \begin{aligned} \displaystyle S &= （底辺）×\color{hotpink}{（高さ）}÷\:2 \\ \\ &= AC\:×\:\color{hotpink}{BH}\:÷\:2 \\ \\ &= \frac{1}{2}\cdot4\cdot\color{hotpink}{3\cdot\sin{60°}} \\ \end{aligned} \)