
今日の板書はこれ!
- 範囲を確認する。
- 単位円を書く。
- \(\sin\) なら \(y\) 座標。\(\cos\) なら \(x\) 座標。\(\tan\) なら \(x=1\) の \(y\) 座標に値をとる。
- 角度を読み取る。
\(0°≦\theta≦180°\) のとき、\(\displaystyle\sin{\theta}=\frac{1}{2}\) を満たす \(\theta\) を求めよ。
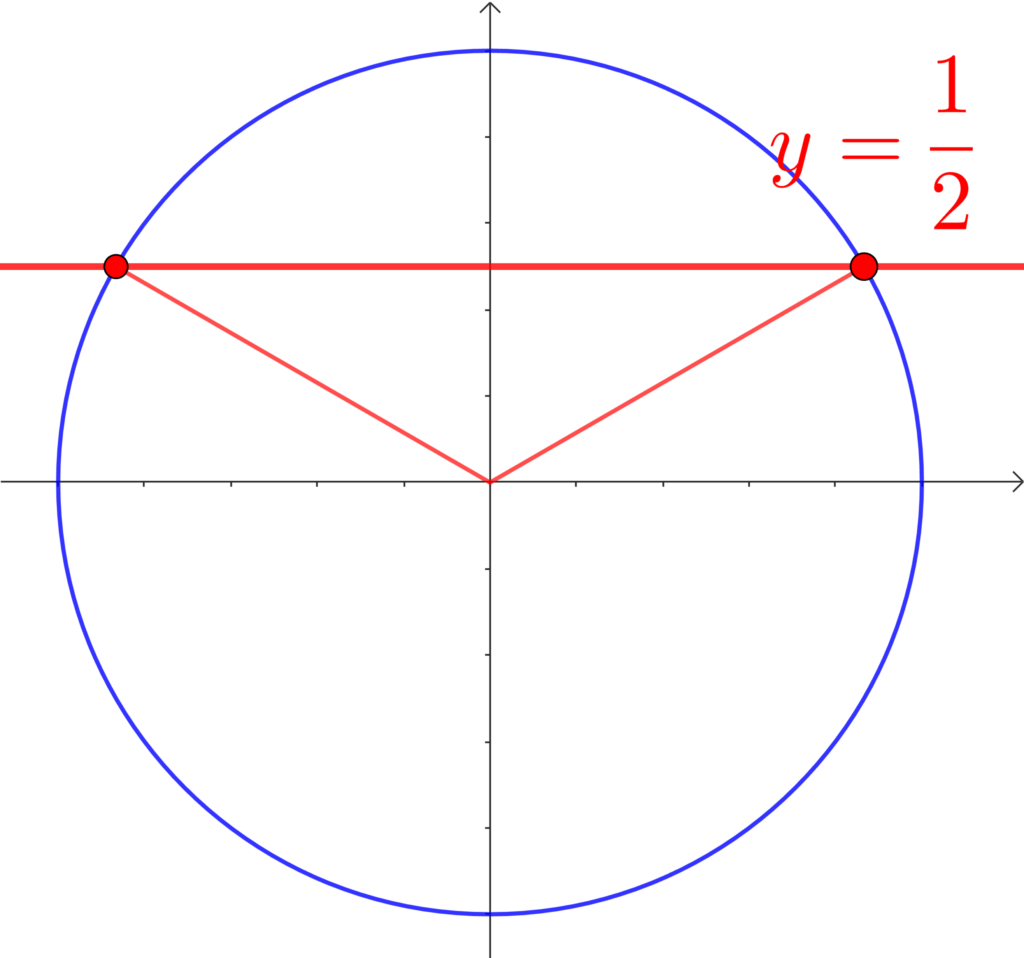
\(\theta=30°, 150°\)
\(0°≦\theta≦180°\) のとき、\(\displaystyle\cos{\theta}=\frac{1}{\sqrt{2}}\) を満たす \(\theta\) を求めよ。
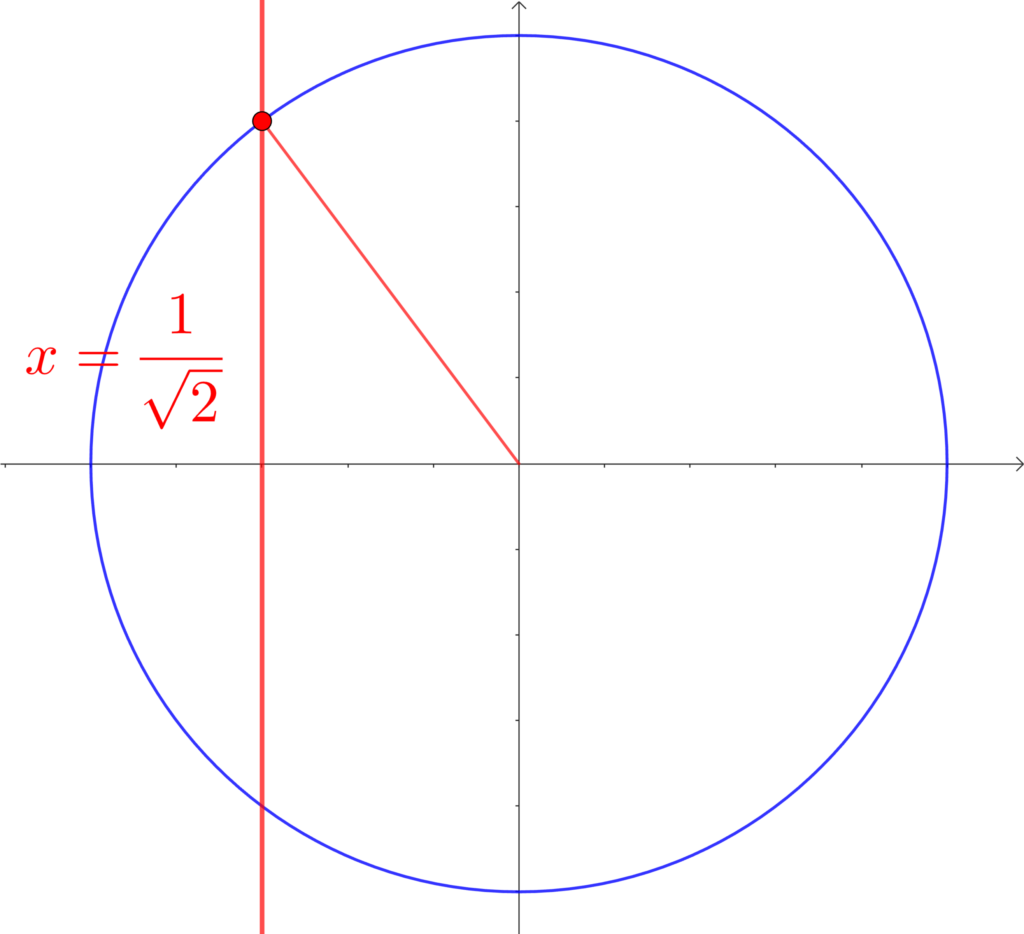
\(\theta=135°\)

もっと詳しく願いします!!
「人より勉強に時間がかかる」と感じていませんか?
私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。
• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」
• 「解答の意味が理解できず、勉強が進まない」
教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。
でも大丈夫!
このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。
「噛み砕き方」がわかれば、文章はぐっと読みやすくなります!
三角比を含む方程式とは?
三角比を含む方程式について説明していきます。

方程式に三角比が入ってるってこと?

そうだね!次のような方程式だよ!
\(0°≦\theta≦180°\) のとき、\(\displaystyle\sin{\theta}=\frac{1}{2}\) を満たす \(\theta\) を求めよ。
\(0°≦\theta≦180°\) のとき、\(\displaystyle\cos{\theta}=\frac{1}{\sqrt{2}}\) を満たす \(\theta\) を求めよ。
まずは、いつもの方程式から。
「方程式 \(x^2-3x-4=0\) を解く」ということは、
「この方程式が成立する \(x\) の値をすべて求める」ということでした。
この方程式の解は \(x=4, -1\) ですので、
\(x\) に \(4\) を代入しても、\(4^2-3\cdot4-4\) で \(0\) に
\(x\) に \(-1\) を代入しても、\((-1)^2-3\cdot(-1)-4\) で \(0\) になります。
三角比を含む方程式もやることは同じ。
「\(\sin{\theta}=\frac{1}{2}\) を解く」ということは、
「この方程式が成立する \(\theta\) の値をすべて求める」ということです。
もっと分かりやすく表現すると、
「\(\sin\) が \(\frac{1}{2}\) になる角度を教えてね!」
ということです。
ただし、「\(\sin\) が \(\frac{1}{2}\) になる角度」はいくらでもあるので、問題文の頭に「\(0°≦\theta≦180°\) のとき」という角度の条件がついています。

そんな難しそうじゃなくて安心した!
三角比を含む方程式の解き方
では実際に解いてみましょう。
\(0°≦\theta≦180°\) のとき、\(\displaystyle\sin{\theta}=\frac{1}{2}\) を満たす \(\theta\) を求めよ。
三角比を含む方程式の解き方は次の4ステップ!
- 範囲を確認する。
- 単位円を書く。
- \(\sin\) なら \(y\) 座標。\(\cos\) なら \(x\) 座標。\(\tan\) なら \(x=1\) の \(y\) 座標に値をとる。
- 角度を読み取る。
1.範囲を確認する
三角比の方程式では、最初に角度の範囲を確認しましょう。
数学Ⅱでは「三角関数」を学びますが、範囲の確認は「むちゃくちゃ重要」です!
今回の例題では「\(0°≦\theta≦180°\) のとき」と言われていますので、「0°から180°の間の角度を考えるんだなぁ」って思いましょう。

今のうちから、角度の範囲を意識できるようになろうね!
2.単位円を書く
角度の範囲を確認したら、次は単位円を書きましょう。
三角比を考えるときは、「常に単位円」で考えます。
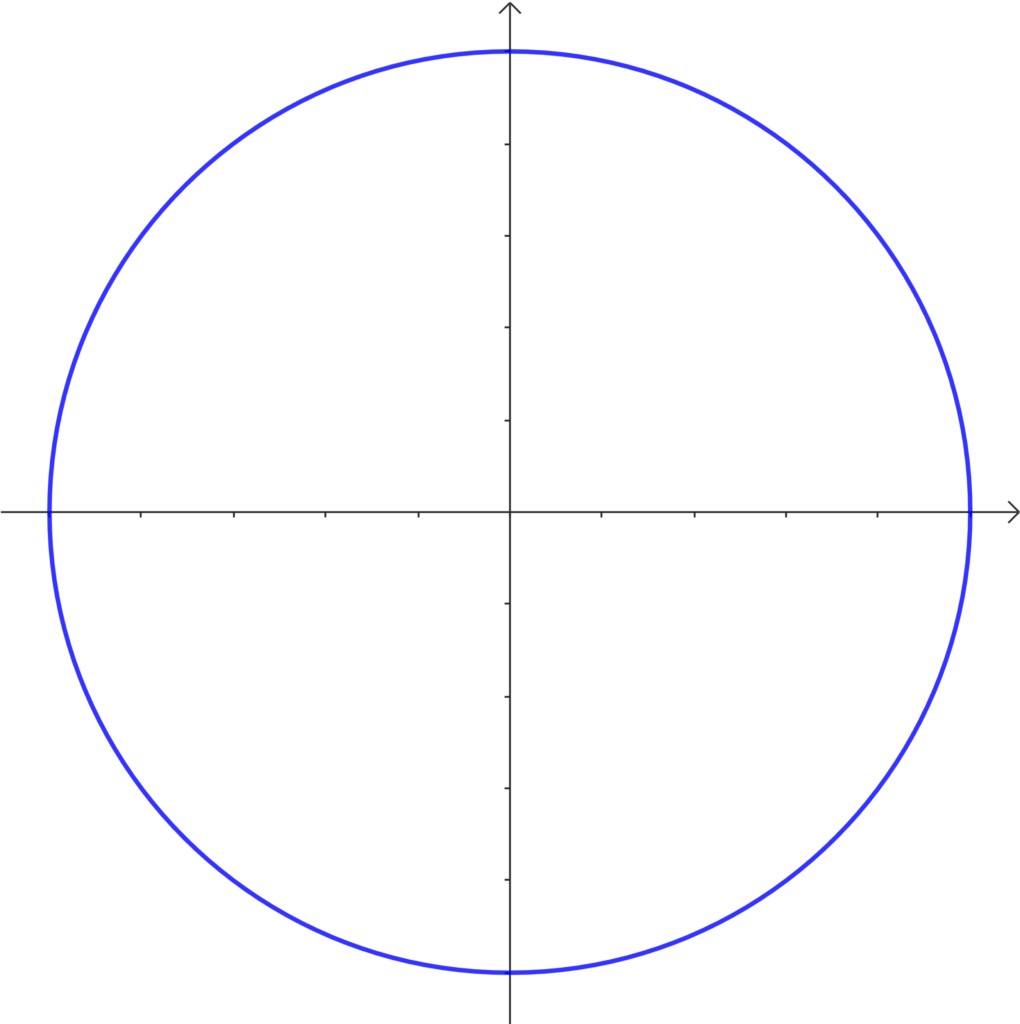
3.sinならy座標。cosならx座標。tanならx=1のy座標に値をとる
次は、さっき書いた単位円に、「三角比の値」を書き込みましょう。
「\(\sin\) なら \(y\) 座標に」、「\(\cos\) なら \(x\) 座標に」、「\(\tan\) なら \(x=1\) の \(y\) 座標」に値を書き込みます。
今回の方程式は「\(\sin{\theta}=\frac{1}{2}\) 」ですから、
\(y\) 座標が \(\frac{1}{2}\) の場所を書き込みます。
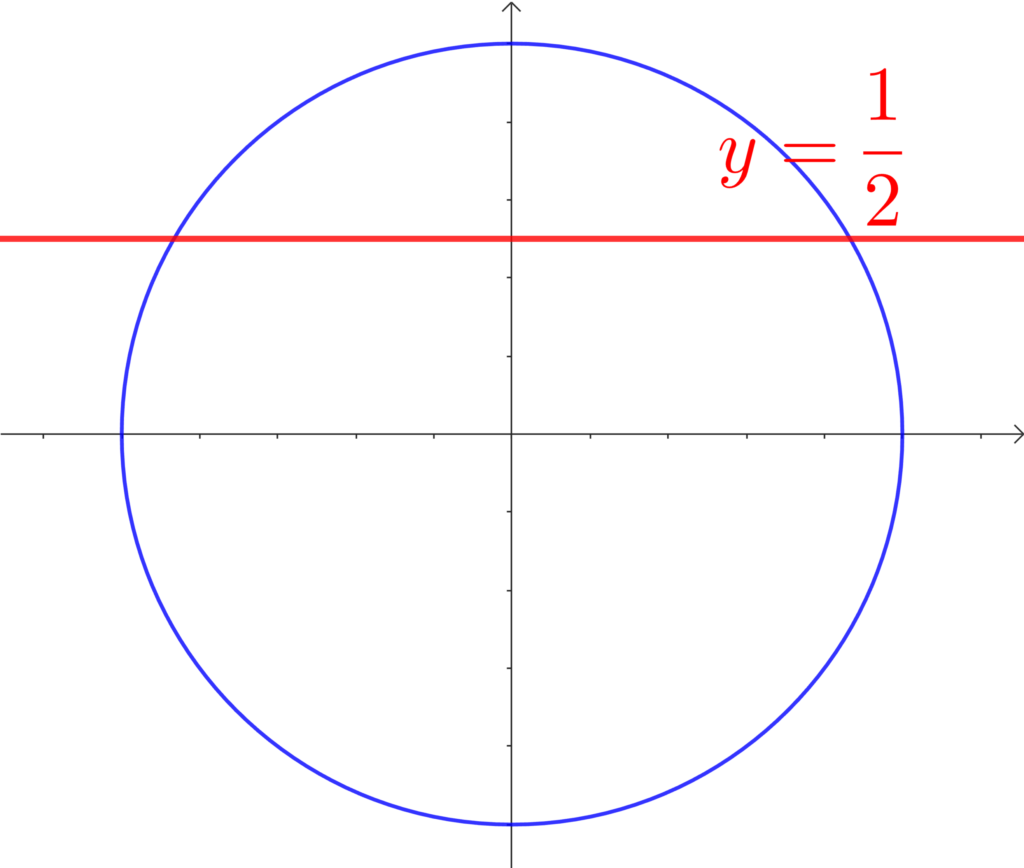
角度を読み取る
最後に、原点と交点を通る線分を書き、角度を読み取ります。
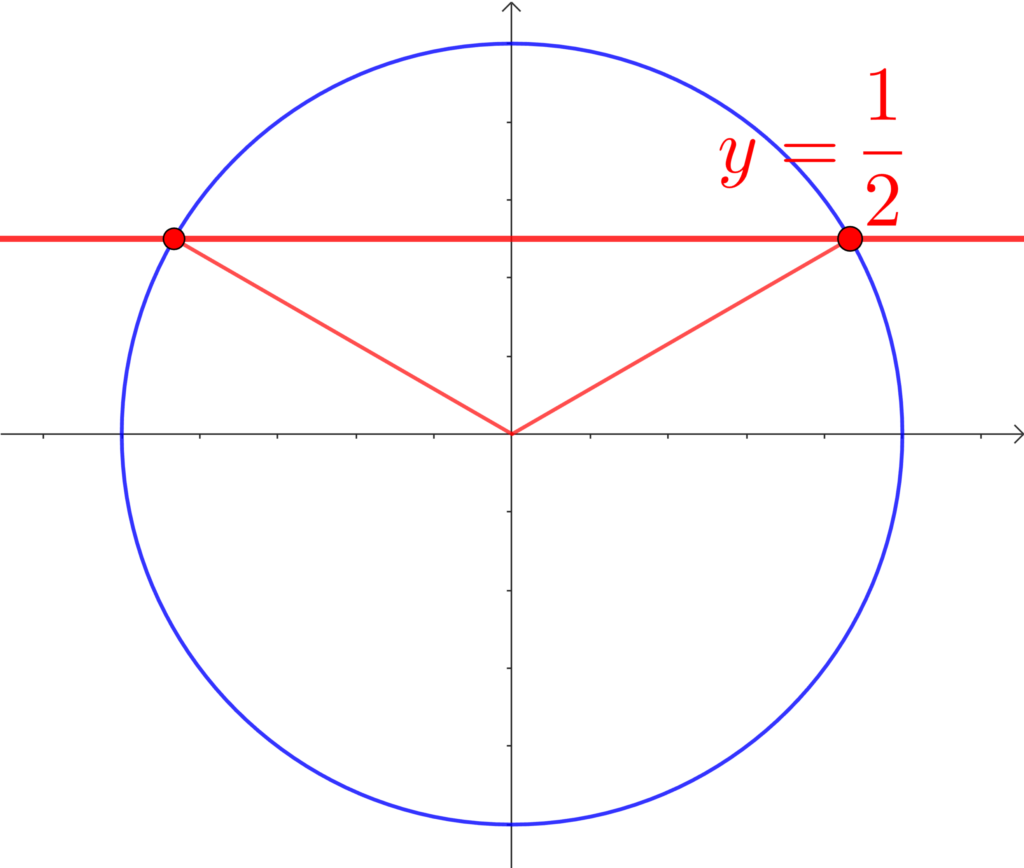
ここでのポイントは、前回で暗記したこれ!
- 30°関連(30°, 60°, 120°, 150°)の三角比
→ 大きさは \(\frac{1}{2}=0.5\) or \(\frac{\sqrt{3}}{2}≒0.9\) 。符号は単位円で考える。
\(\sin\) が \(\frac{1}{2}\) の値をとるときは、30°関連(30°, 60°, 120°, 150°)のときでした。
単位円をもう一度見てみてください。
「候補は30°, 60°, 120°, 150°」のどれかです。
何度に見えますか?

んー何度に見える?って言われてもな•••
では、\(\sin\) が \(\frac{\sqrt{3}}{2}\) になるときの、単位円と比べてみましょう。

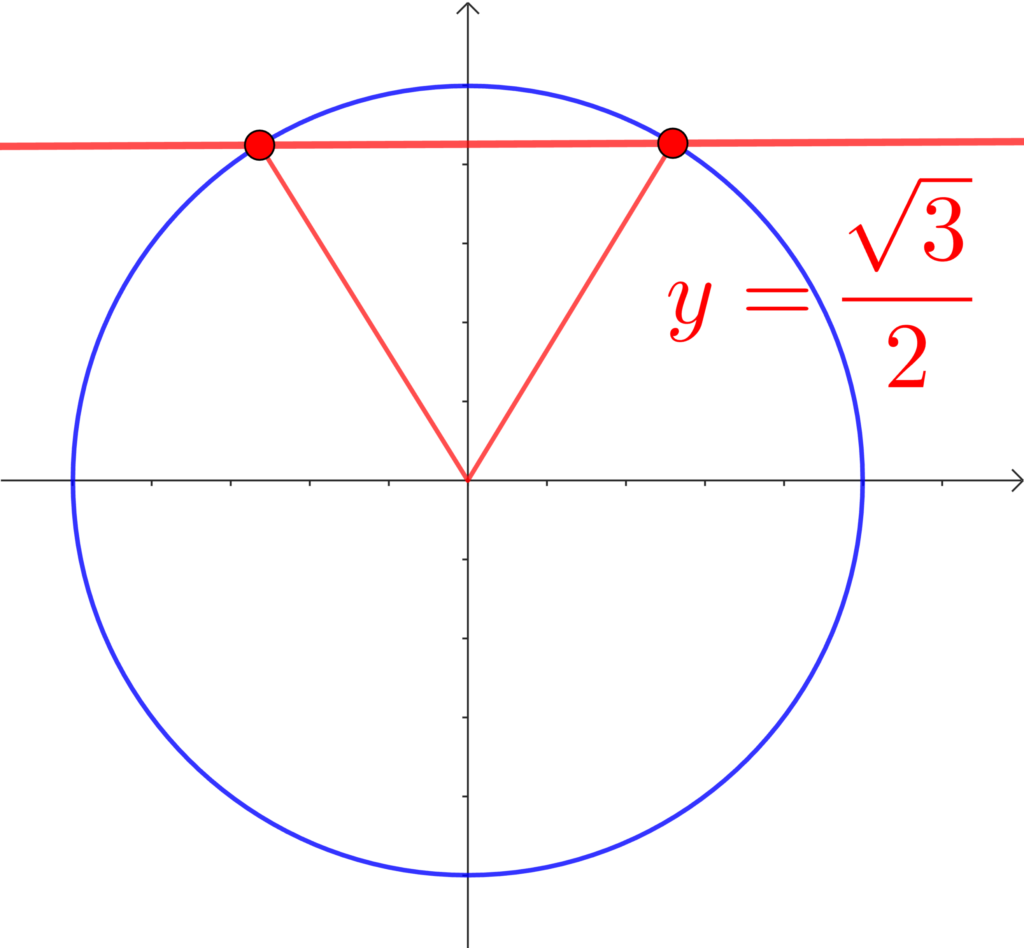
もう一度。「候補は30°, 60°, 120°, 150°」のどれかです。
何度に見えますか?

あ!左が30°と150°で、右が60°と120°!

その通り!!
「\(\sin\) が \(\frac{1}{2}\) の大きさ」になる角度は、「30°, 60°, 120°, 150°のどれか」ですから、\(\theta=30°, 150°\) と分かります。
単位円がちゃんと書けてれば、すぐに判断することができますね。
例題で定着させよう!
では、もう1問チャレンジして、三角比の方程式を完璧にしましょう。
\(0°≦\theta≦180°\) のとき、\(\displaystyle\cos{\theta}=\frac{1}{\sqrt{2}}\) を満たす \(\theta\) を求めよ。
角度の確認し、単位円を書き、\(x\) 座標が \frac{1}{\sqrt{2}} の場所を書き込みます。


範囲が \(0°≦\theta≦180°\) だから、下の交点は範囲外になるからね!

あ、確かに!気をつけなきゃ。
あとは、角度を読み取るだけです。
- 45°関連(45°, 135°)の三角比
→ 大きさは \(\frac{1}{\sqrt{2}}\) 。符号は単位円で考える。
\(\cos\) の大きさが \frac{1}{\sqrt{2}} になるのは、角度が45°関連(45°, 135°)のときなので、
すぐに、\(\theta=135°\) と判断することができます。

あとで \(\tan\)の問題もやってみよ!
まとめ:三角比を含む方程式

さて、今回のまとめだよ!
三角比を含む方程式の解き方を勉強しました。
- 範囲を確認する。
- 単位円を書く。
- \(\sin\) なら \(y\) 座標。\(\cos\) なら \(x\) 座標。\(\tan\) なら \(x=1\) の \(y\) 座標に値をとる。
- 角度を読み取る。
\(0°≦\theta≦180°\) のとき、\(\displaystyle\sin{\theta}=\frac{1}{2}\) を満たす \(\theta\) を求めよ。

\(\theta=30°, 150°\)
\(0°≦\theta≦180°\) のとき、\(\displaystyle\cos{\theta}=\frac{1}{\sqrt{2}}\) を満たす \(\theta\) を求めよ。

\(\theta=135°\)

また一つ賢くなった!







コメント