
今日の板書はこれ!


| θ | 30° | 45° | 60° |
|---|---|---|---|
| \(\sin{\theta}\) | \(\displaystyle\frac{1}{2}\) | \(\displaystyle\frac{1}{\sqrt{2}}\) | \(\displaystyle\frac{\sqrt{3}}{2}\) |
| \(\cos{\theta}\) | \(\displaystyle\frac{\sqrt{3}}{2}\) | \(\displaystyle\frac{1}{\sqrt{2}}\) | \(\displaystyle\frac{1}{2}\) |
| \(\tan{\theta}\) | \(\displaystyle\frac{1}{\sqrt{3}}\) | \(1\) | \(\sqrt{3}\) |

詳しく願いします!!
「人より勉強に時間がかかる」と感じていませんか?
私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。
• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」
• 「解答の意味が理解できず、勉強が進まない」
教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。
でも大丈夫!
このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。
「噛み砕き方」がわかれば、文章はぐっと読みやすくなります!
有名角 30°, 45°, 60° の三角比

30°, 45°, 60° の三角比を考えよう!

三角比ってなんだけ?
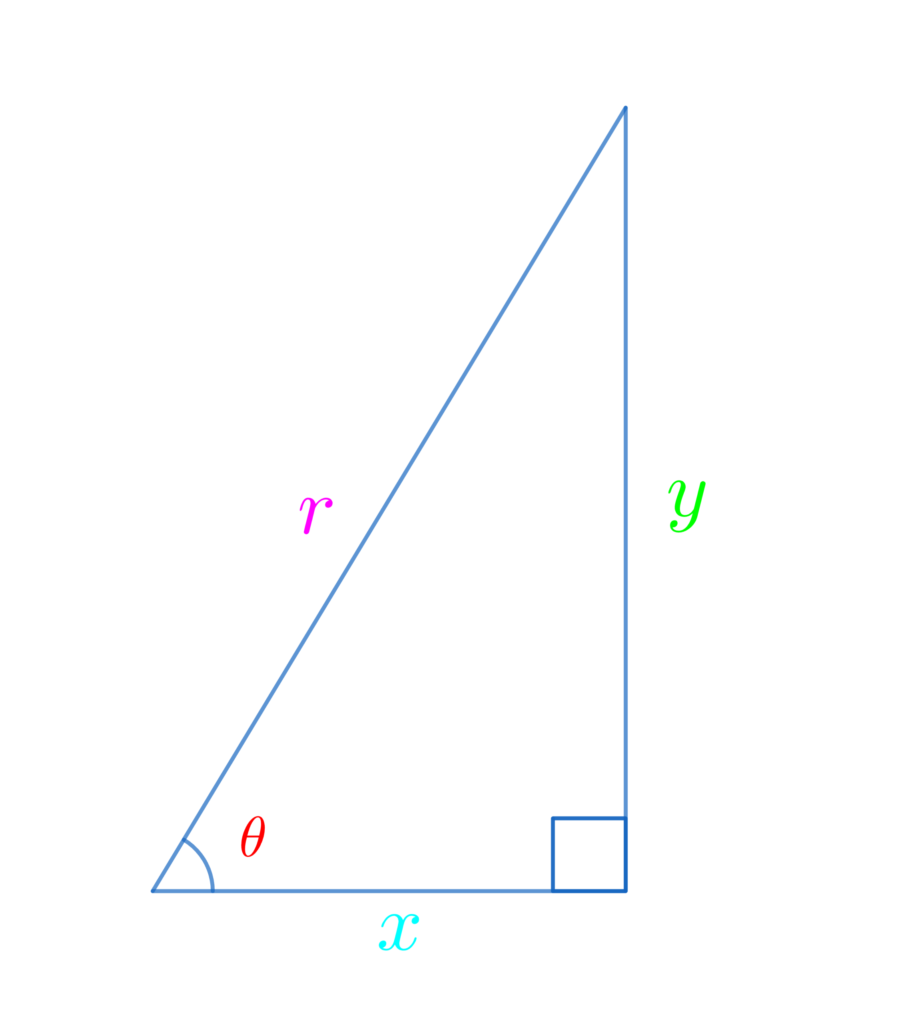
三角比は「ある角度θを持つ直角三角形の2辺の比の値」のこと。
\(\displaystyle\color{red}{\cos{\theta}}=\frac{\color{deepskyblue}{底辺}}{\color{hotpink}{斜辺}}=\frac{\color{deepskyblue}{x}}{\color{hotpink}{r}}\)
\(\displaystyle\color{red}{\cos{\theta}}=\frac{\color{deepskyblue}{底辺}}{\color{hotpink}{斜辺}}=\frac{\color{deepskyblue}{x}}{\color{hotpink}{r}}\)
\(\displaystyle\color{red}{\tan{\theta}}=\frac{\color{lime}{対辺}}{\color{deepskyblue}{底辺}}=\frac{\color{lime}{y}}{\color{deepskyblue}{x}}\)
そして、次の直角三角形であれば、辺の比は知っていますね。
- 30°, 60°, 90° の直角三角形の辺の比は \(1:2:\sqrt{3}\)
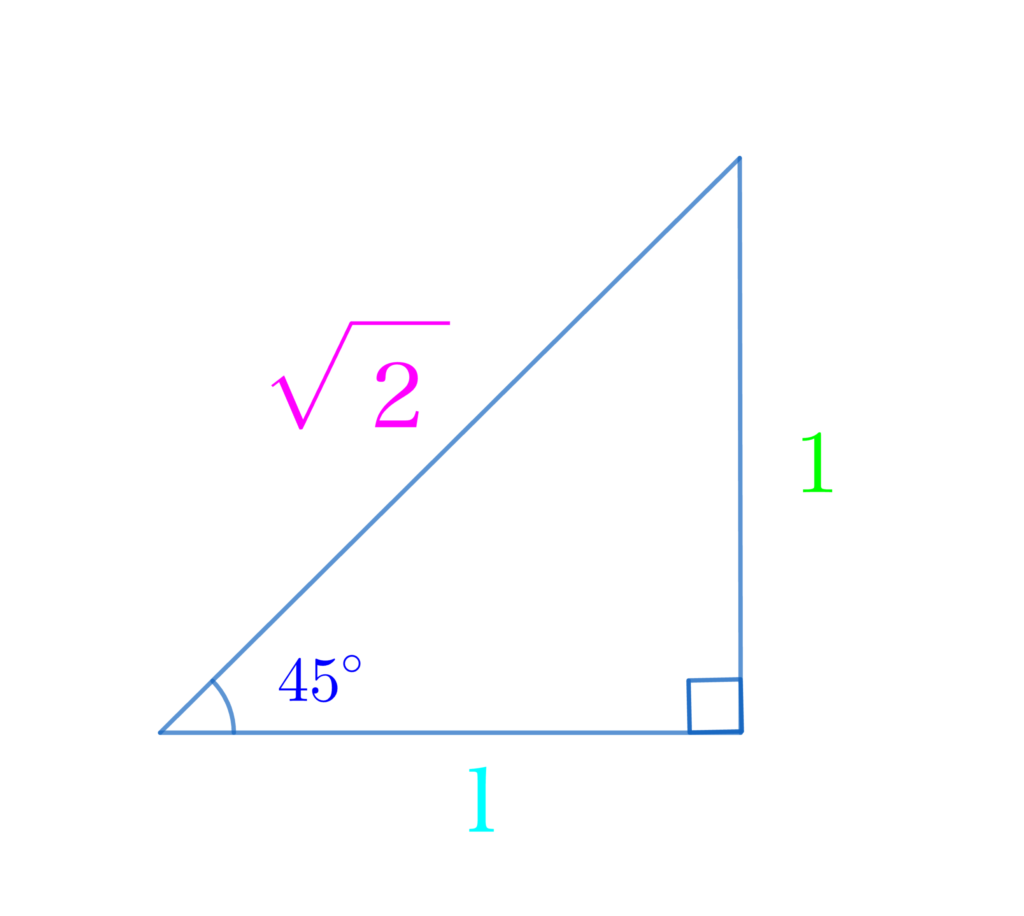
- 45°, 45°, 90° の直角三角形の辺の比は \(1:1:\sqrt{2}\)



30°の三角比
まずは、30°の三角比から。
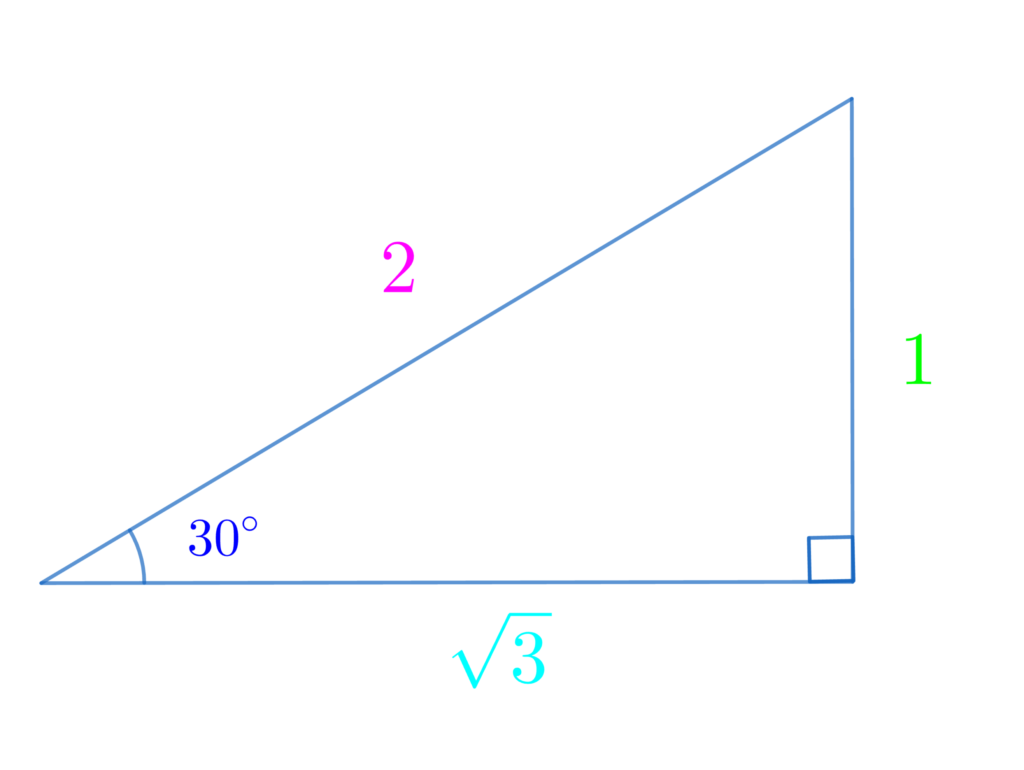
\(\displaystyle\color{red}{\sin{\theta}}=\frac{\color{lime}{対辺}}{\color{hotpink}{斜辺}}=\frac{\color{lime}{1}}{\color{hotpink}{2}}\)
\(\displaystyle\color{red}{\cos{\theta}}=\frac{\color{deepskyblue}{底辺}}{\color{hotpink}{斜辺}}=\frac{\color{deepskyblue}{\sqrt{3}}}{\color{hotpink}{2}}\)
\(\displaystyle\color{red}{\tan{\theta}}=\frac{\color{lime}{対辺}}{\color{deepskyblue}{底辺}}=\frac{\color{lime}{1}}{\color{deepskyblue}{\sqrt{3}}}\)
45°の三角比
次は、45°の三角比。
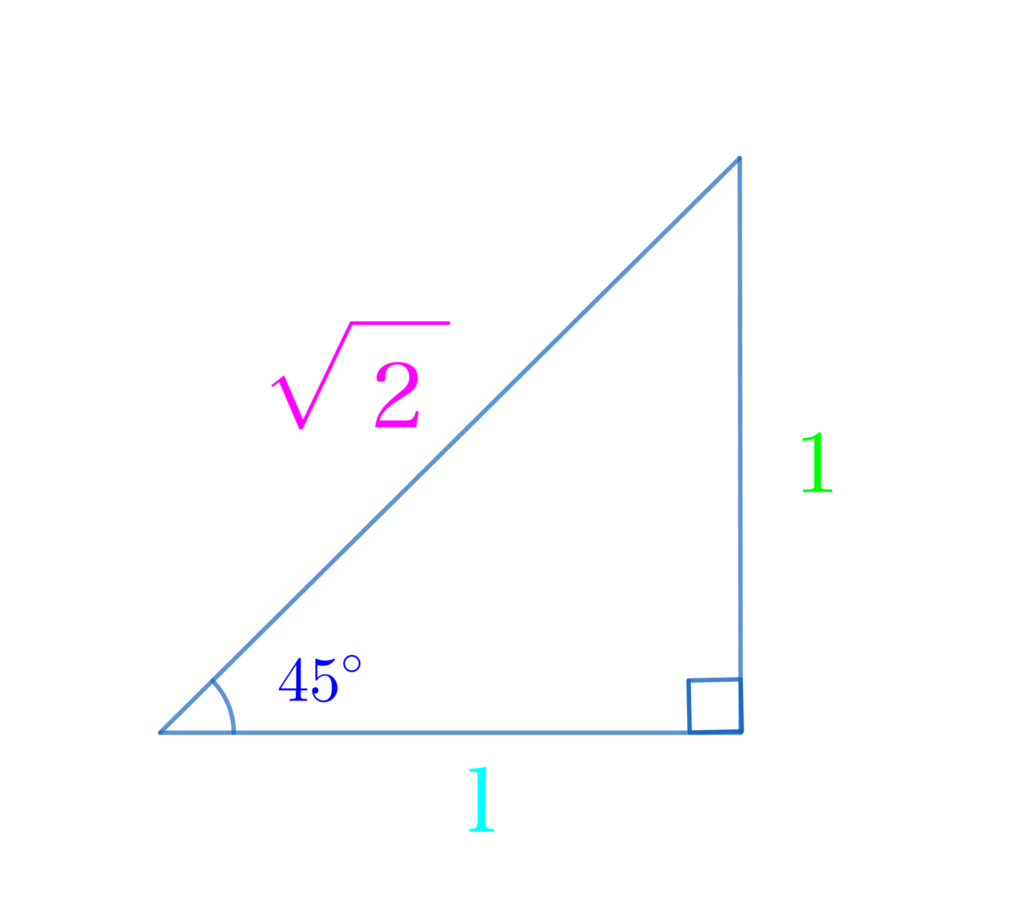
\(\displaystyle\color{red}{\sin{\theta}}=\frac{\color{lime}{対辺}}{\color{hotpink}{斜辺}}=\frac{\color{lime}{1}}{\color{hotpink}{\sqrt{2}}}\)
\(\displaystyle\color{red}{\cos{\theta}}=\frac{\color{deepskyblue}{底辺}}{\color{hotpink}{斜辺}}=\frac{\color{deepskyblue}{1}}{\color{hotpink}{\sqrt{2}}}\)
\(\displaystyle\color{red}{\tan{\theta}}=\frac{\color{lime}{対辺}}{\color{deepskyblue}{底辺}}=\frac{\color{lime}{1}}{\color{deepskyblue}{1}}=1\)
60°の三角比
最後に、60°の三角比。
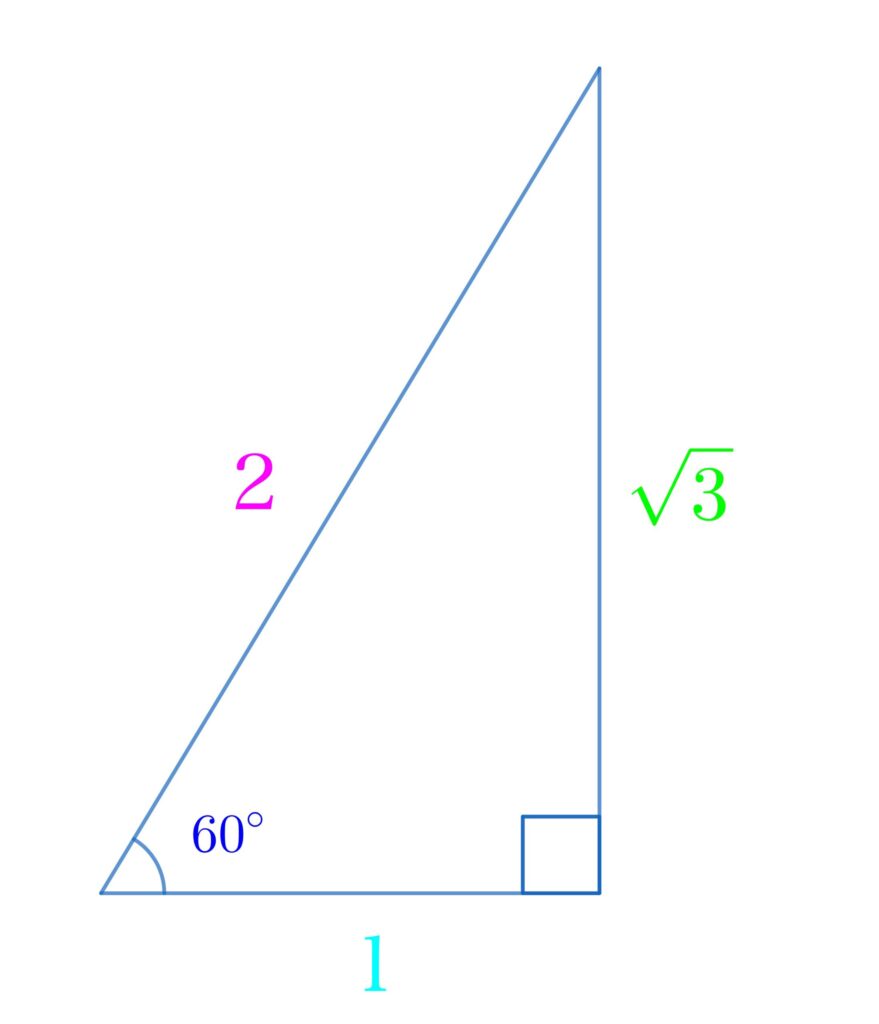
\(\displaystyle\color{red}{\sin{\theta}}=\frac{\color{lime}{対辺}}{\color{hotpink}{斜辺}}=\frac{\color{lime}{\sqrt{3}}}{\color{hotpink}{2}}\)
\(\displaystyle\color{red}{\cos{\theta}}=\frac{\color{deepskyblue}{底辺}}{\color{hotpink}{斜辺}}=\frac{\color{deepskyblue}{1}}{\color{hotpink}{2}}\)
\(\displaystyle\color{red}{\tan{\theta}}=\frac{\color{lime}{対辺}}{\color{deepskyblue}{底辺}}=\frac{\color{lime}{\sqrt{3}}}{\color{deepskyblue}{1}}=\sqrt{3}\)
三角比の表

表にまとめるとこんな感じ!
| θ | 30° | 45° | 60° |
|---|---|---|---|
| \(\sin{\theta}\) | \(\displaystyle\frac{1}{2}\) | \(\displaystyle\frac{1}{\sqrt{2}}\) | \(\displaystyle\frac{\sqrt{3}}{2}\) |
| \(\cos{\theta}\) | \(\displaystyle\frac{\sqrt{3}}{2}\) | \(\displaystyle\frac{1}{\sqrt{2}}\) | \(\displaystyle\frac{1}{2}\) |
| \(\tan{\theta}\) | \(\displaystyle\frac{1}{\sqrt{3}}\) | \(1\) | \(\sqrt{3}\) |
表を自分で作ってみる。
次の表を自分で書けるようにしましょう!
| θ | 30° | 45° | 60° |
|---|---|---|---|
| \(\sin{\theta}\) | |||
| \(\cos{\theta}\) | |||
| \(\tan{\theta}\) |
実際にやってみましょう。
\(\theta\) が \(30°\) の 直角三角形を書き\(\sin{30°}\)、\(\cos{30°}\)、\(\tan{30°}\) を考える。

\(\theta\) が \(45°\) の 直角三角形を書き、\(\sin{45°}\)、\(\cos{30°}\)、\(\tan{45°}\) を考える。

\(\theta\) が \(60°\) の 直角三角形を書き、\(\sin{60°}\)、\(\cos{60°}\)、\(\tan{60°}\)を考える。

どうですか?
表は書けるようになりましたか?

んー時間をかければできるかも。

「できるかも」じゃなくて、「できる」にしてね!
覚え方
次は、直角三角形を書かなくても表が作れるようにしましょう。

今から5分で暗記!!
| θ | 30° | 45° | 60° |
|---|---|---|---|
| \(\sin{\theta}\) | \(\displaystyle\frac{1}{2}\) | \(\displaystyle\frac{1}{\sqrt{2}}\) | \(\displaystyle\frac{\sqrt{3}}{2}\) |
| \(\cos{\theta}\) | \(\displaystyle\frac{\sqrt{3}}{2}\) | \(\displaystyle\frac{1}{\sqrt{2}}\) | \(\displaystyle\frac{1}{2}\) |
| \(\tan{\theta}\) | \(\displaystyle\frac{1}{\sqrt{3}}\) | \(1\) | \(\sqrt{3}\) |
私は次のように整理し、暗記しています。
- 30°, 60°の値は \(\displaystyle\frac{1}{2}=0.5\) or \(\displaystyle\frac{\sqrt{3}}{2}\approx0.9\)
- 45°の値は \(\displaystyle\frac{1}{\sqrt{2}}\)
- 30°, 60°の値は \(\displaystyle\frac{1}{\sqrt{3}}\approx0.6\) or \(\sqrt{3}\approx1.7\)
- 45°の値は \(1\)

おー。覚えやすいかも。
まとめ:有名角 30°, 45°, 60° の三角比

さて、今回のまとめだよ!
有名角 30°, 45°, 60° の三角比は暗記しておこう!!



| θ | 30° | 45° | 60° |
|---|---|---|---|
| \(\sin{\theta}\) | \(\displaystyle\frac{1}{2}\) | \(\displaystyle\frac{1}{\sqrt{2}}\) | \(\displaystyle\frac{\sqrt{3}}{2}\) |
| \(\cos{\theta}\) | \(\displaystyle\frac{\sqrt{3}}{2}\) | \(\displaystyle\frac{1}{\sqrt{2}}\) | \(\displaystyle\frac{1}{2}\) |
| \(\tan{\theta}\) | \(\displaystyle\frac{1}{\sqrt{3}}\) | \(1\) | \(\sqrt{3}\) |

また一つ賢くなった!






コメント