
今日の板書はこれ!
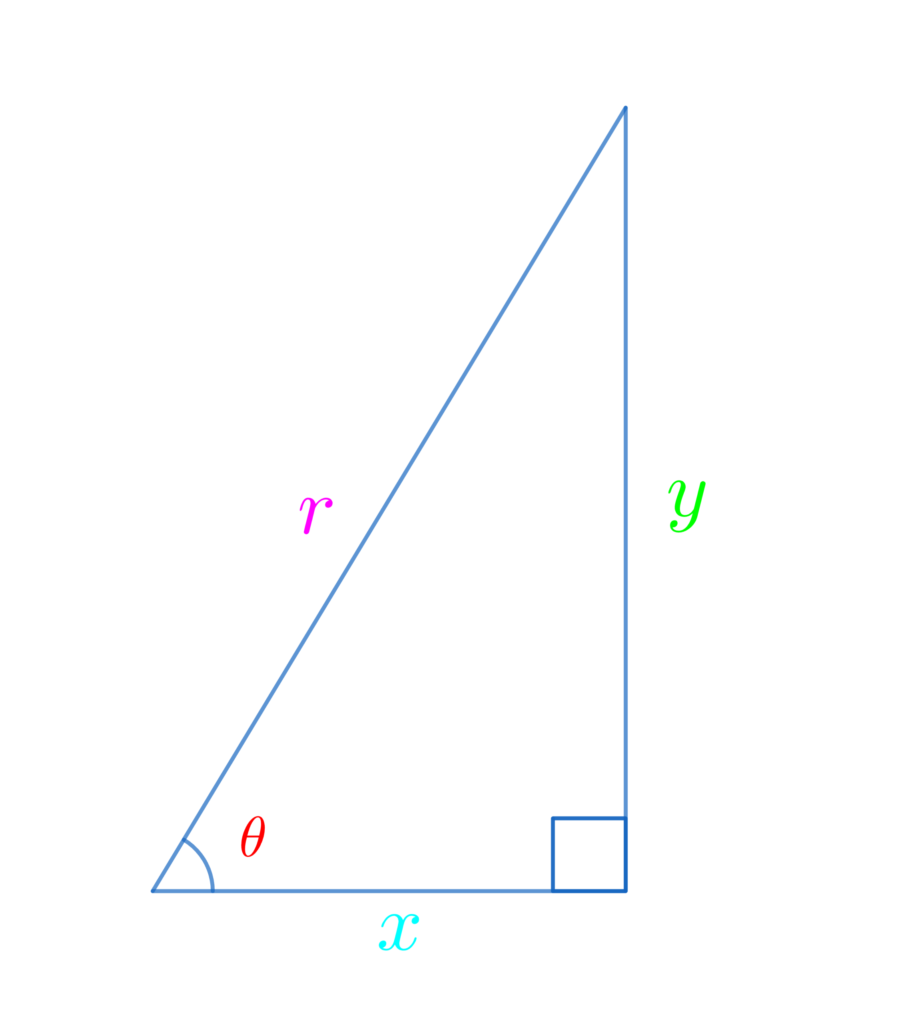
\(\displaystyle\color{red}{\sin{\theta}}=\frac{\color{lime}{対辺}}{\color{hotpink}{斜辺}}=\frac{\color{lime}{y}}{\color{hotpink}{r}}\)
\(\displaystyle\color{red}{\cos{\theta}}=\frac{\color{deepskyblue}{底辺}}{\color{hotpink}{斜辺}}=\frac{\color{deepskyblue}{x}}{\color{hotpink}{r}}\)
\(\displaystyle\color{red}{\tan{\theta}}=\frac{\color{lime}{対辺}}{\color{deepskyblue}{底辺}}=\frac{\color{lime}{y}}{\color{deepskyblue}{x}}\)

詳しく願いします!!
「人より勉強に時間がかかる」と感じていませんか?
私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。
• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」
• 「解答の意味が理解できず、勉強が進まない」
教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。
でも大丈夫!
このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。
「噛み砕き方」がわかれば、文章はぐっと読みやすくなります!
三角比とは

三角比ってなに?

三角比は「ある角度θを持つ直角三角形の2辺の比の値」のことだよ!
三角比のポイントは、
「1つの角度が \(\theta\) である全ての直角三角形は、辺の比が等しい」
ということです。

んー•••。どゆこと?
下の図の、「直角三角形」について、辺の比を比べてみましょう。
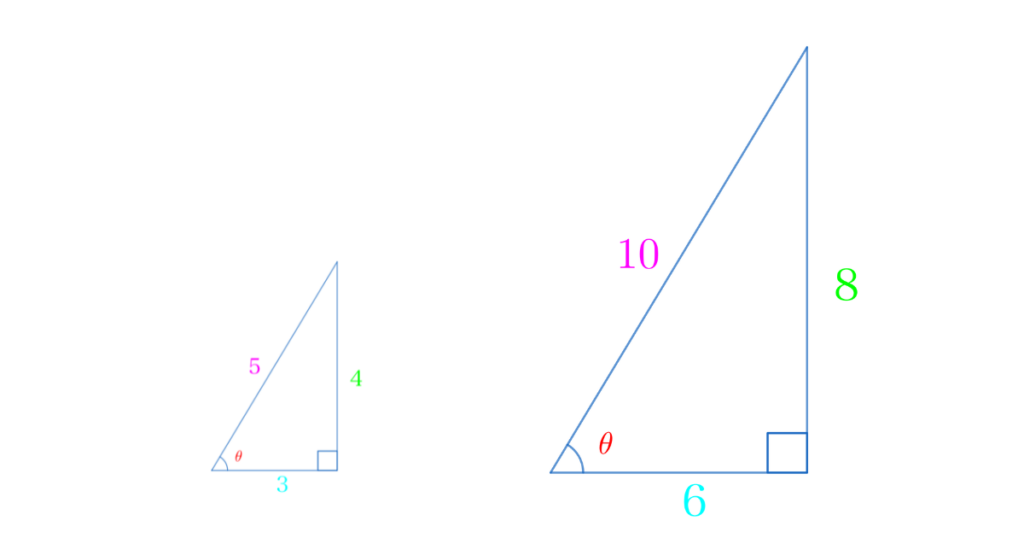
直角三角形は、直角を持つ三角形です。
そして、他の角度 \(\theta\) が等しければ、「2組の角、\(\theta\) と \(90°\) が 等しい三角形」であるため、相似な三角形だといえます。
さらに、三角形の辺の比を比べてみると、
左の直角三角形は
\(\color{deepskyblue}{底辺}: \color{hotpink}{斜辺}:\color{lime}{対辺}= \color{deepskyblue}{3}:\color{hotpink}{4}:\color{lime}{5}\)
右の直角三角形も
\(\color{deepskyblue}{底辺}: \color{hotpink}{斜辺}:\color{lime}{対辺} = \color{deepskyblue}{6}:\color{hotpink}{8}:\color{lime}{10} = \color{deepskyblue}{3}:\color{hotpink}{4}:\color{lime}{5}\)
つまり、「1つの角度が \(\theta\) である全ての直角三角形は、辺の比が等しい」というわけです。

どんなけ大きい直角三角形でも、どんなけ小さい直角三角形でも、角度θが同じだったら、辺の比も同じになるんだ!

ここまでは理解したよ!それで三角比ってなんだっけ?
三角比は、ある角度θを持つ直角三角形の2辺の比の値のことです。
3辺のうち、2辺を用いた比を、扱いやすい分数の形で定義してあります。
\(\sin{\theta}\) の定義
\(\displaystyle\color{red}{\sin{\theta}}=\frac{\color{lime}{対辺}}{\color{hotpink}{斜辺}}=\frac{\color{lime}{y}}{\color{hotpink}{r}}\)

\(\color{red}{\sin{\theta}}\) とは、ある角度θを持つ直角三角形の2辺 \(\color{hotpink}{斜辺r}\) と \(\color{lime}{対辺y}\) の 比の値です。
分母が \(\color{hotpink}{斜辺 r}\) 、分子が \(\color{lime}{対辺 y}\) です。

直角三角形は、θが左下、直角が右下に来るようにセットしようね!
例えば、

この直角三角形において、 \(\color{red}{\sin{\theta}}\) の値は
\(\displaystyle\color{red}{\sin{\theta}}=\frac{\color{lime}{4}}{\color{hotpink}{5}}\)
となります。
\( \sin{\theta} \) は 正弦 と表現することもあります。
\(\cos{\theta}\) の定義
\(\displaystyle\color{red}{\cos{\theta}}=\frac{\color{deepskyblue}{底辺}}{\color{hotpink}{斜辺}}=\frac{\color{deepskyblue}{x}}{\color{hotpink}{r}}\)

\(\color{red}{\cos{\theta}}\) とは、ある角度θを持つ直角三角形の2辺 \(\color{hotpink}{斜辺r}\) と \(\color{deepskyblue}{底辺x}\) の 比の値です。
分母が \(\color{hotpink}{斜辺 r}\) 、分子が \(\color{deepskyblue}{底辺x}\) です。

直角三角形は、θが左下、直角が右下に来るようにセットしようね!(2回目!)
例えば、

この直角三角形において、 \(\color{red}{\cos{\theta}}\) の値は
\(\displaystyle\color{red}{\cos{\theta}}=\frac{\color{deepskyblue}{3}}{\color{hotpink}{5}}\)
となります。
\(\cos{\theta}\) は 余弦 と表現することもあります。
\(\tan{\theta}\) の定義
\(\displaystyle\color{red}{\tan{\theta}}=\frac{\color{lime}{対辺}}{\color{deepskyblue}{底辺}}=\frac{\color{lime}{y}}{\color{deepskyblue}{x}}\)

\(\color{red}{\tan{\theta}}\) とは、ある角度θを持つ直角三角形の2辺 \(\color{deepskyblue}{底辺x}\) と \(\color{lime}{対辺y}\)の 比の値です。
分母が \(\color{deepskyblue}{底辺x}\)、分子が \(\color{lime}{対辺 y}\) です。

直角三角形は、θが左下、直角が右下に来るようにセットしようね!(3回目!)
例えば、

この直角三角形において、 \(\color{red}{\tan{\theta}}\) の値は
\(\displaystyle\color{red}{\tan{\theta}}=\frac{\color{lime}{4}}{\color{deepskyblue}{3}}\)
となります。
\(\tan{\theta}\) は 正接と表現することもあります。
三角比の表とは
三角比の表というのがあります。
それがこちら。
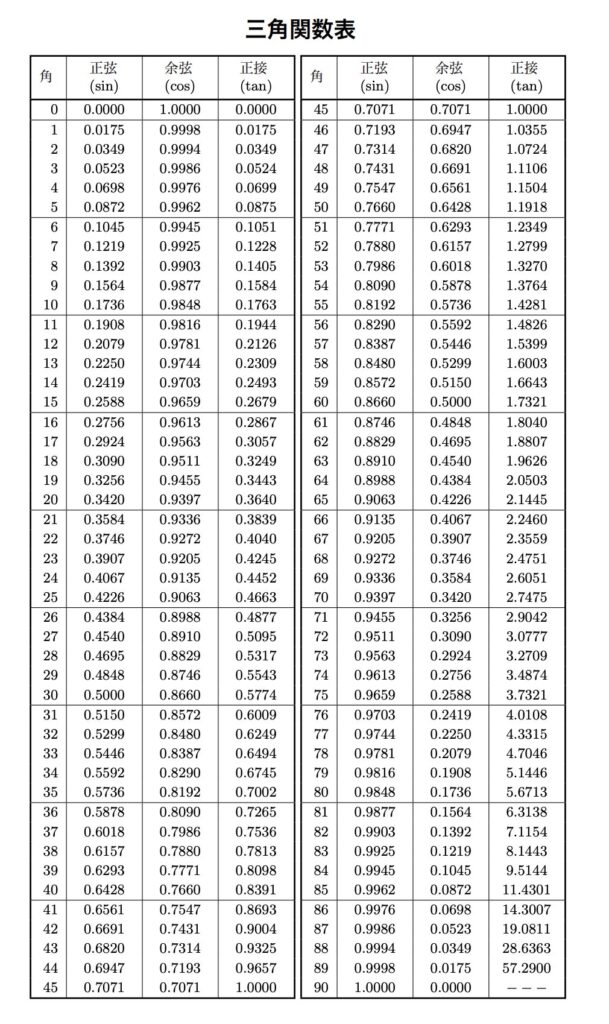
https://www.math.s.chiba-u.ac.jp/~yasuda/sysKOU/cit-H20/trig-table.pdf

うわ。数字ばっかりで酔いそう。
この表からは、「角θの三角比の値」と「三角比の値から角θのおおよその値」を読み取ることができます。
三角比の表から「角θの三角比の値」を読み取る。
例えば、角10° の三角比 \(\sin{10°}, \cos{10°}, \tan{10°}\) は
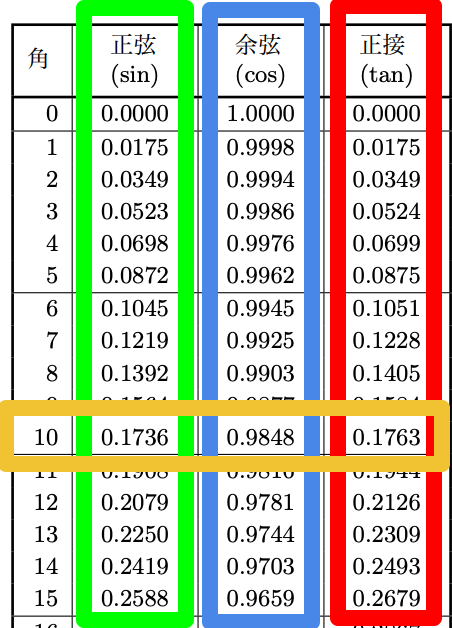
\(\sin{10°}=0.1736\)
\(\cos{10°}=0.9848\)
\(\tan{10°}=0.1763\)
と読み取ることができます。
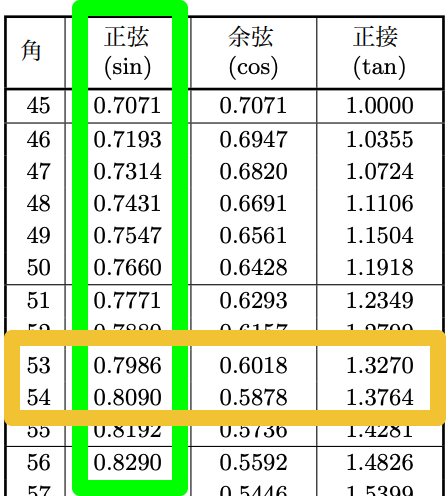
三角比の表から「三角比の値から角θのおおよその値」を読み取る。
例えば、次の直角三角形の角θの値は

\(\displaystyle\color{red}{\sin{\theta}}=\frac{\color{lime}{4}}{\color{hotpink}{5}}=\color{red}{0.8}\)
ですので、三角比の表より
\(\theta \neq 53°\)
と読み取ることができます。
まとめ:直角三角形を用いた三角比の定義

さて、今回のまとめだよ!
三角比は、ある角度θを持つ直角三角形の2辺の比の値のこと。
\(\displaystyle\color{red}{\cos{\theta}}=\frac{\color{deepskyblue}{底辺}}{\color{hotpink}{斜辺}}=\frac{\color{deepskyblue}{x}}{\color{hotpink}{r}}\)
\(\displaystyle\color{red}{\cos{\theta}}=\frac{\color{deepskyblue}{底辺}}{\color{hotpink}{斜辺}}=\frac{\color{deepskyblue}{x}}{\color{hotpink}{r}}\)
\(\displaystyle\color{red}{\tan{\theta}}=\frac{\color{lime}{対辺}}{\color{deepskyblue}{底辺}}=\frac{\color{lime}{y}}{\color{deepskyblue}{x}}\)


また一つ賢くなった!






コメント