【数学Ⅰ】2次関数09：文字を含む2次関数の最大・最小①（関数固定で区間の一端が動く）

---

---

現役教員として数学を教えている「さん」と申します。

「場合分けが苦手」という生徒の多くは、「いつ、なぜ場合分けが発生するのか」という基準に迷っています。

今回は、文字 \(a\) によって定義域が広がっていくとき、最小値のがどのタイミングで入れ替わるのかを論理的に解説します。

教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。

でも大丈夫！

このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。

一見複雑なこの問題を、頂点と端点の関係性から紐解いていきましょう！

文字を含む2次関数の最大・最小①（関数固定で区間の一端が動く）

状況の整理：何が固定で、何が変化するか？

まずは、問題文から「動かないもの」と「動くもの」を明確に区別します。

• 固定（不変）：関数(\(y=x^2-4x+1\)) と 区間の左端(\(x=0\))
• 変化（変動）：定義域の右端(\(x=a\))

つまり、左端 \(x=0\) は固定されたまま、右端 \(x=a\) が右側へ伸びていく状況です。

手順①：変化しないものを図示する

まずは、変化しないもの（関数(\(y=x^2-4x+1\)) と 区間の左端(\(x=0\))）を図示していきます。

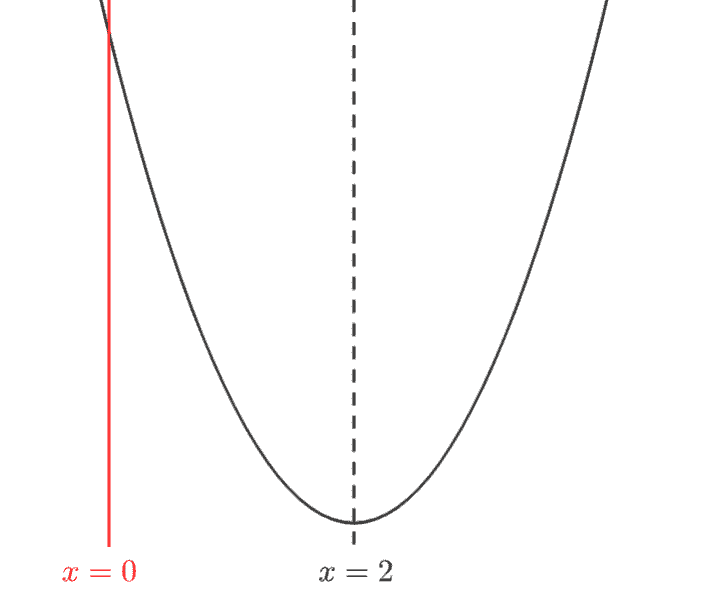
手順②：変化するもの動かす

次に、変化するもの（区間の右端(\(x=a\)) ）を左から動かしていき、区間内での最小値を考えます。

\(a\) は正の定数ですから、\(0\) より右側からスタートします。

【ケース1】軸より左側にあるとき（0<a<2）

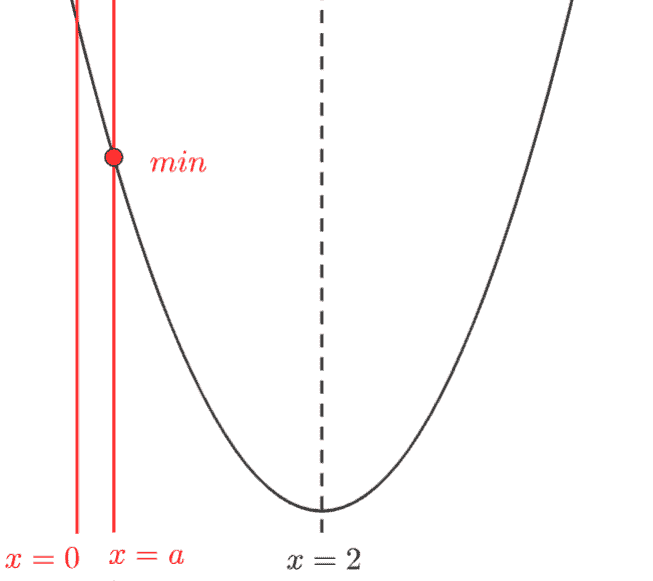
このとき、\(x=a\) で最小値をとります。

最初値：\(x=a\) を代入して \(y=a^2-4a+1\)

ここから、\(x=a\) を右に動かしてみましょう。

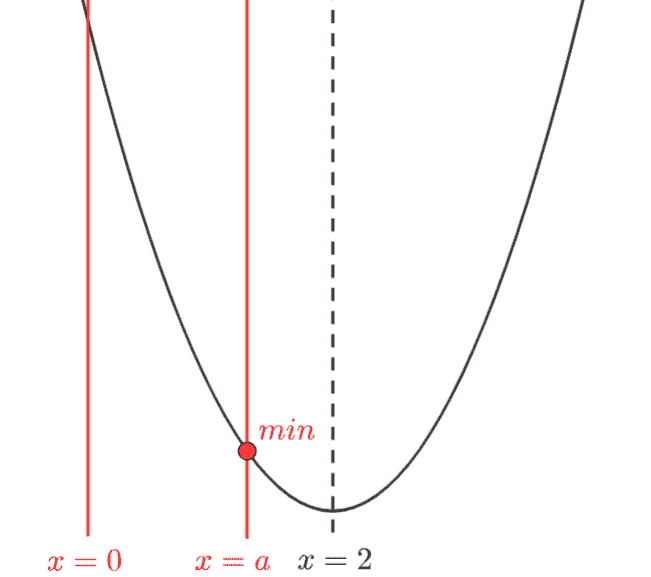
このときも同様に \(x=a\) で最小値をとります。

【ケース2】 軸より右側にあるとき（a≧2）

もう少し、動かしていきます。

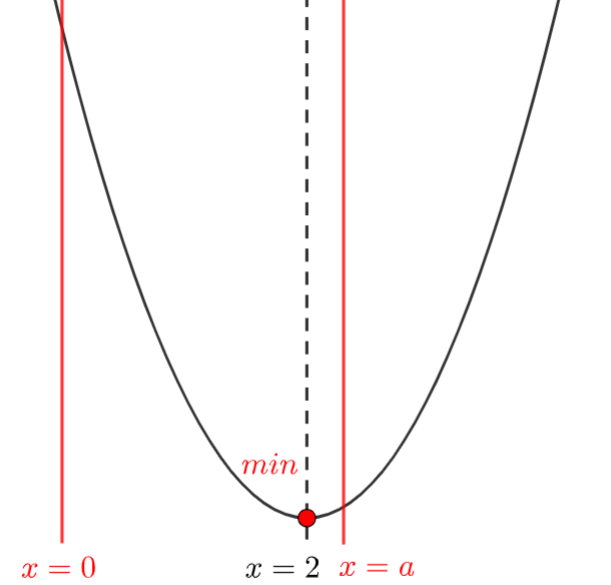
最小値をとるときの \(x\) の値が \(x=2\) に変わりました。

最小値は： \(x=2\)　を代入して \(y=2^2-4\cdot 2+1=-3\)

さらに動かしていきます。

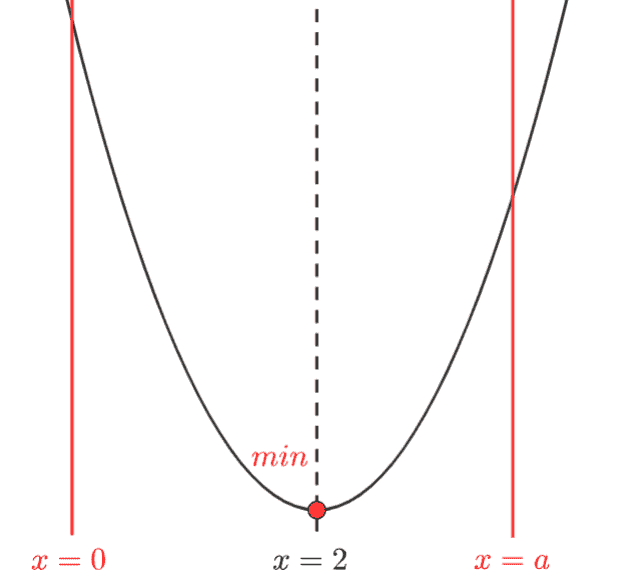
このときも、 \(x=2\) で最小値をとります。

これより右に動かしても、最小値の場所は変わりません。

まとめ：解答の構成

これらをまとめると、以下のようになります。

\(0<a<2\) のとき \(x=a\) で最小値 \(a^2-4a+1\)

\(a≧2\) のとき \(x=a\) で最小値 \(-3\)

まとめ：文字を含む2次関数の最大・最小①（関数固定で区間の一端が動く）

---

---