【数学Ⅰ】2次関数01：関数の値、定義域・値域と最大・最小

---

---

現役教員として数学を教えている「さん」と申します。

「人より勉強に時間がかかる」と感じていませんか？

私の学校にも、同じ悩みを抱えて苦しんでる生徒がたくさんいます。

教科書や参考書の内容を理解するには、「自分なりに噛み砕いて考える力」が必要です。

でも大丈夫！

このサイトでは、私が受けた質問や、つまずきポイントをもとに、わかりやすく解説していきます。

意味から理解し、噛み砕き方をマスターしましょう！！

関数の値、定義域・値域と最大・最小

関数の値

関数とは

\(y=3x-2\) や \(y=\frac{1}{x}\)、\(y=3x^2-5x+4\) のような式を関数といいます。

関数とは、ある値を入れると、それに対応する値を返してくれる仕組みのことです。

「入力した数をもとに、結果（出力）を決めるルール」と考えるとわかりやすいです。

例：y=3x-2

関数\(y=3x-2\)に、\(x=2\) を入れると、\(y=3×2-2=4\) となります。

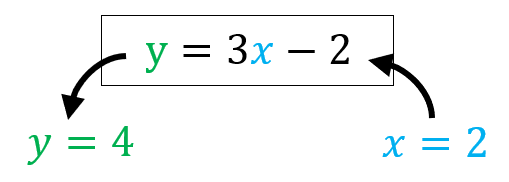
同じように、\(x=-2\) を入れると、\(y=3×(-2)-2=-8\) が返ってきます。

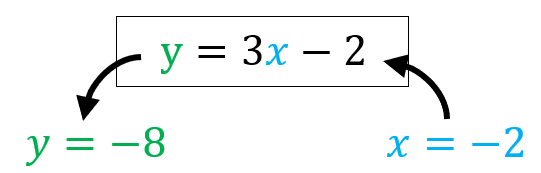
関数の表し方と値

関数は、\(y=f(x)\) と表すこともあります。

このとき、\(x=a\) を入れたときの値を \(f(a)\) と表します。

つまり、関数\(y=f(x)\)に \(x=a\) を代入したときの値 が \(f(a)\) です。

例題

---

(1) \(f(x)=x^2+2x\) に \(x=5\) を代入します。

---

(2) 同じように、\(x=a-1\) を代入します。

「\(a-1\)」は１つの数字として扱うため、必ずかっこ \(a-1\) をつけることが大切です。

定義域・値域と最大・最小

関数\(y=f(x)\)において変数\(x\)がとりうる値の範囲を定義域といいます。

また、\(x\)が定義域内のすべての値をとるとき、\(f(x)\)がとりうる値の範囲を値域といいます。

では次の例題で最大値と最小値を考えていきましょう。

例題

最大値・最小値とは、値域（\(y\)の範囲）の最大値・最小値のことです。

最大・最小を考える際には、必ずグラフと定義域を描き、視覚的に考えましょう。

---

(1) \(y=-2x+3 \:(-1≦x<2)\) のグラフ次のようになります。

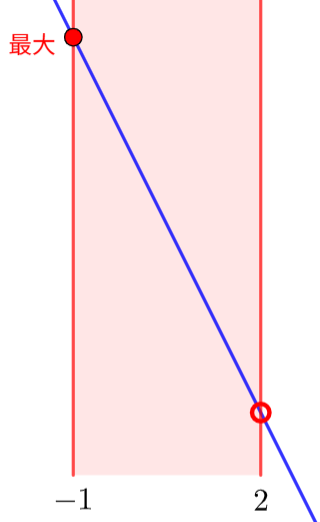
よって、\(x=-1\) のとき最大値 \(y=-2\cdot(-1)+3=5\)

\(x=2\) は定義域に含まれないため、「最小値なし」となります。

---

(2) \(y=x^2\: (-2≦x≦1)\) のグラフ次のようになります。

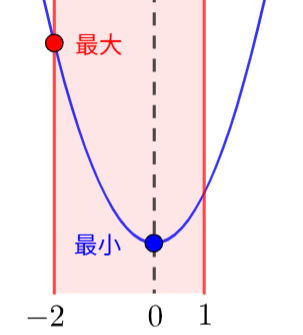
よって、\(x=2\) のとき最大値 \(y=2^2=4\)

\(x=2\) のとき最大値 \(y=2^2=4\)

---

(3) \(\displaystyle y=\frac{1}{x} \:(1<x≦2)\) のグラフ次のようになります。

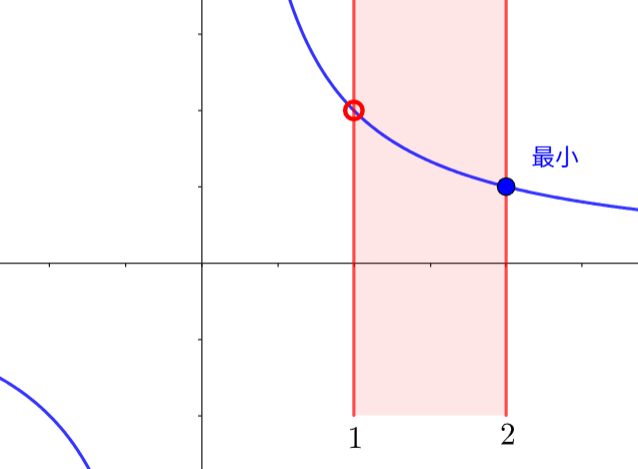
よって、最大値なし

\(x=2\) のとき最小値 \(\displaystyle y=\frac{1}{2}\)

まとめ：関数の値、定義域・値域と最大・最小

---

---