【高校数学Ⅰ】「2次関数」まとめページ｜定義・公式を分かりやすく完全解説

関数
\(x\)の値を定めると\(y\)の値がただ１つ定まるとき、\(y\)は\(x\)の関数であるという。\(y\)が\(x\)の関数であることを\(y=f(x)\)と表すことが多い。関数\(y=f(x)\)において、\(x=a\)のときの\(y\)の値を\(f(a)\)と表す。

座標平面
平面を直交する数直線で4つの象限に分けたもの。右上から反時計回りに第1象限、第2象限、第3象限、第4象限という。なお、座標軸上はどの象限でもない。

定義域
関数\(y=f(x)\)において変数\(x\)がとりうる値の範囲。

値域
\(x\)が定義域内のすべての値をとるとき、\(f(x)\)がとりうる値の範囲。

最大・最小
グラフと定義域を描き、視覚的に考える。

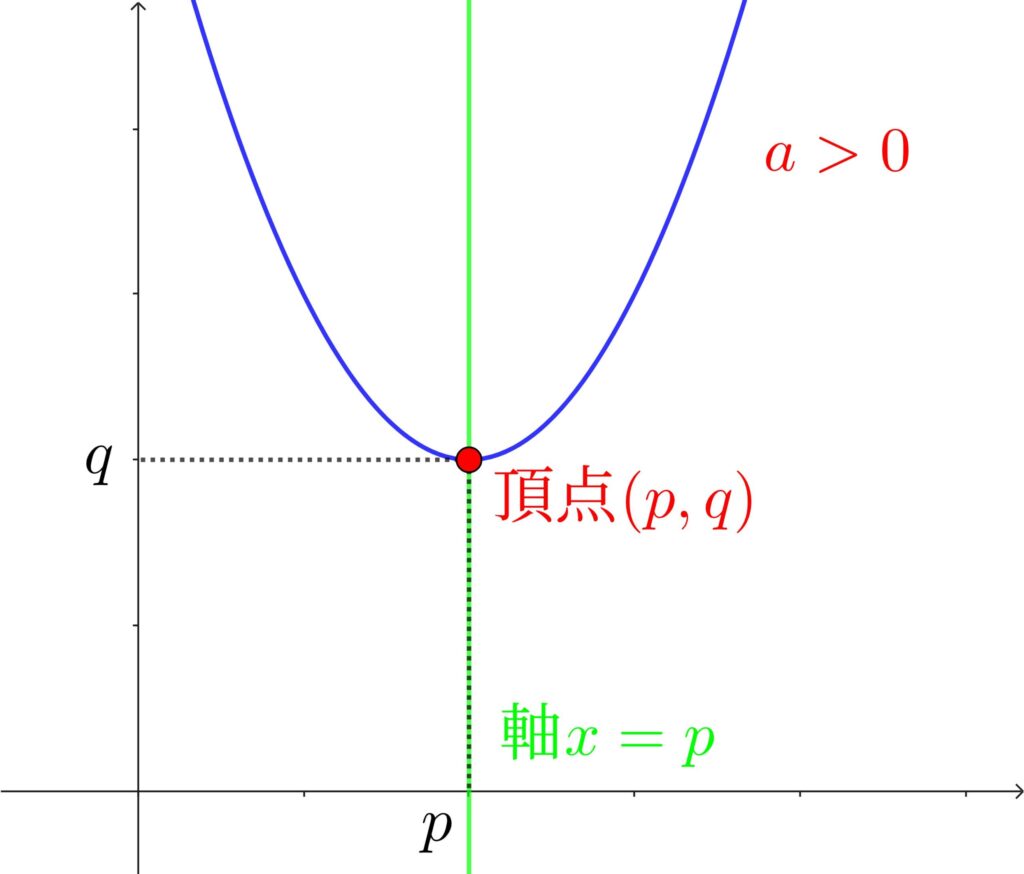
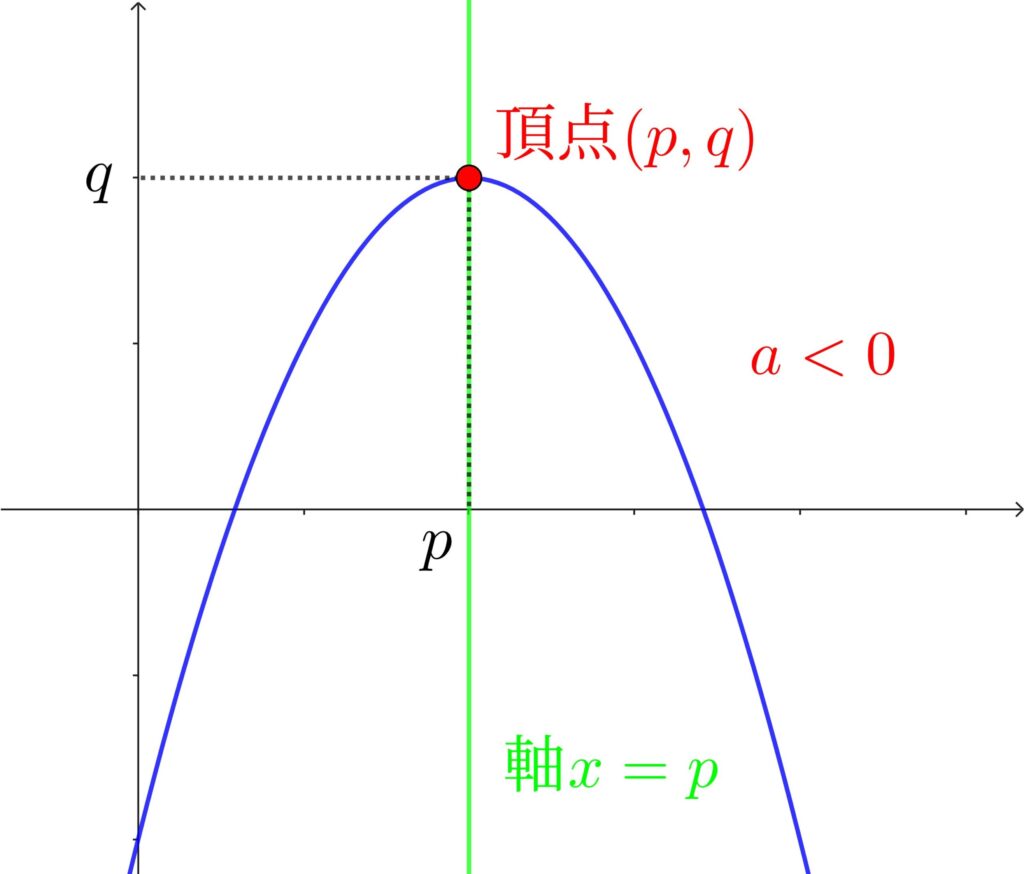
2次関数\(y=a{(x-p)}^2+q\) のグラフは、\(a>0\) のとき下に凸、\(a<0\) のとき上に凸の放物線になる。
また、頂点は \((p,q)\) 、軸は \(x=p\) の放物線である。

平方完成とは、\(ax^2+bx+c\) を \(a(x-p)^2+q\) に変形すること。

1. \(x^2\) の係数でくくる　（定数項（最後の数字）は無視！）
2. カッコ内を2乗の形に　（「半分」にして「2乗を引く」！）
3. カッコを外して整理　（分配法則の計算ミスに注意！）

1. 平方完成をして \(y = a(x – p)^2 + q\) の形にする
2. 頂点は \((p, q)\) 、軸は \(x = p\)
3. \(y\) 軸との交点は「元の式」に \(x=0\) を入れて求める

軸の方程式：\(x=-\frac{b}{2a}\)

関数 \(y=f(x)\) を\(x\) 軸方向に \(p\)、\(y\) 軸方向に \(q\)平行移動した関数を \(y=g(x)\) とする。

\(g(x)\)の上の点 \((x,y)\) を逆に平行移動した点 \((x-p,y-q)\)

これを \(y=f(x)\) に代入した条件式 \(y-q=f(x-p)\) 、これが移動後の関数 \(y=g(x)\)。

\(y=f(x)\) を \(x\) 軸、\(y\) 軸、原点に関して対称移動した関数 \(y=g(x)\)

• \(x\) 軸対称：\(-y=f(x)\)
• \(y\) 軸対称：\(y=f(-x)\)
• 原点対称：\(-y=f(-x)\)

1. 平方完成をして、頂点を求める。
2. グラフを描く。（「上に凸」か「下に凸」か注意！）
3. 定義域（\(x\) の範囲）をグラフに描き込み、一番高い所と低い所を探す。

1. 平方完成をする（ \(c\) はそのまま残しておく）。
2. グラフを描き、最大・最小をとる場所を特定する。
3. その場所の値を計算し、問題文の数字とイコールで結ぶ（方程式を作る）。

何が一定で何が変化するのかを意識する。

• 一定：関数(\(y=x^2-4x+1\)) と 区間の左端(\(x=0\))
• 変化：区間の右端(\(x=a\))

解答の手順

1. 最初に変化しないものを図示する。
2. 次に、変化するものを左から動かしていき、区間内での最大・最小を考える。最大・最小をとるときの \(x\) の値が変わる瞬間に着目し、場合分けする。