
今日の板書はこれ!
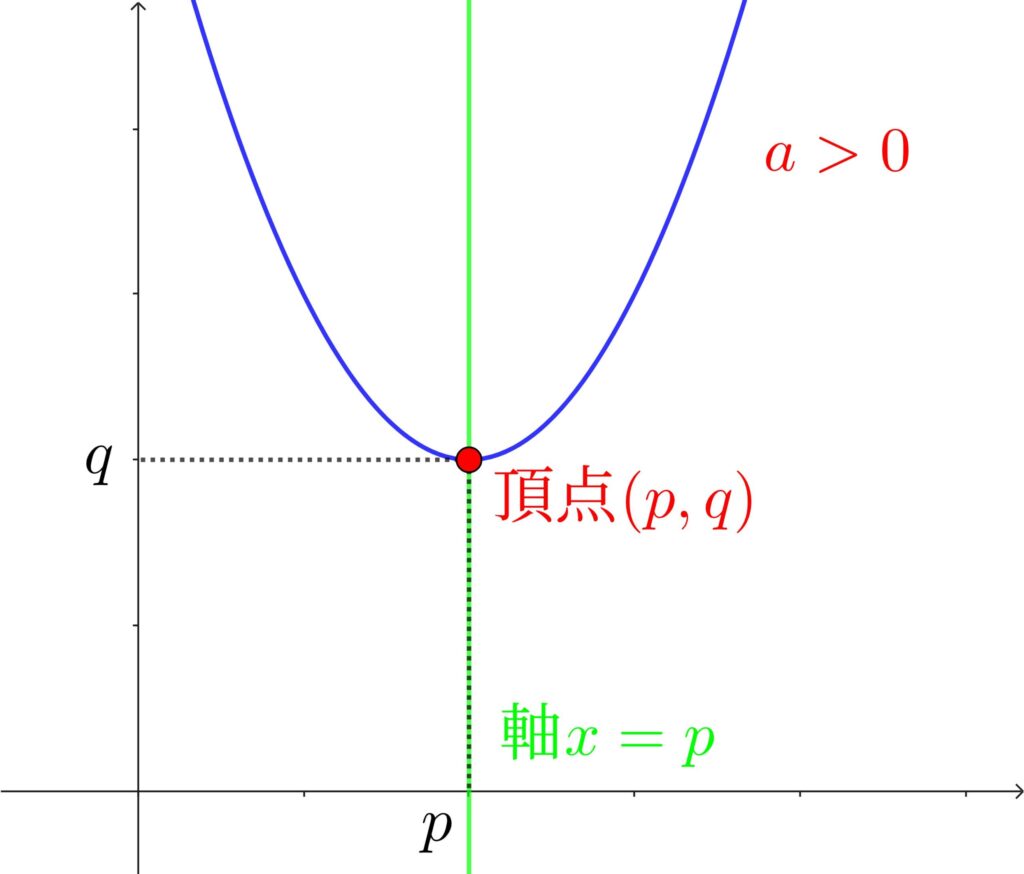
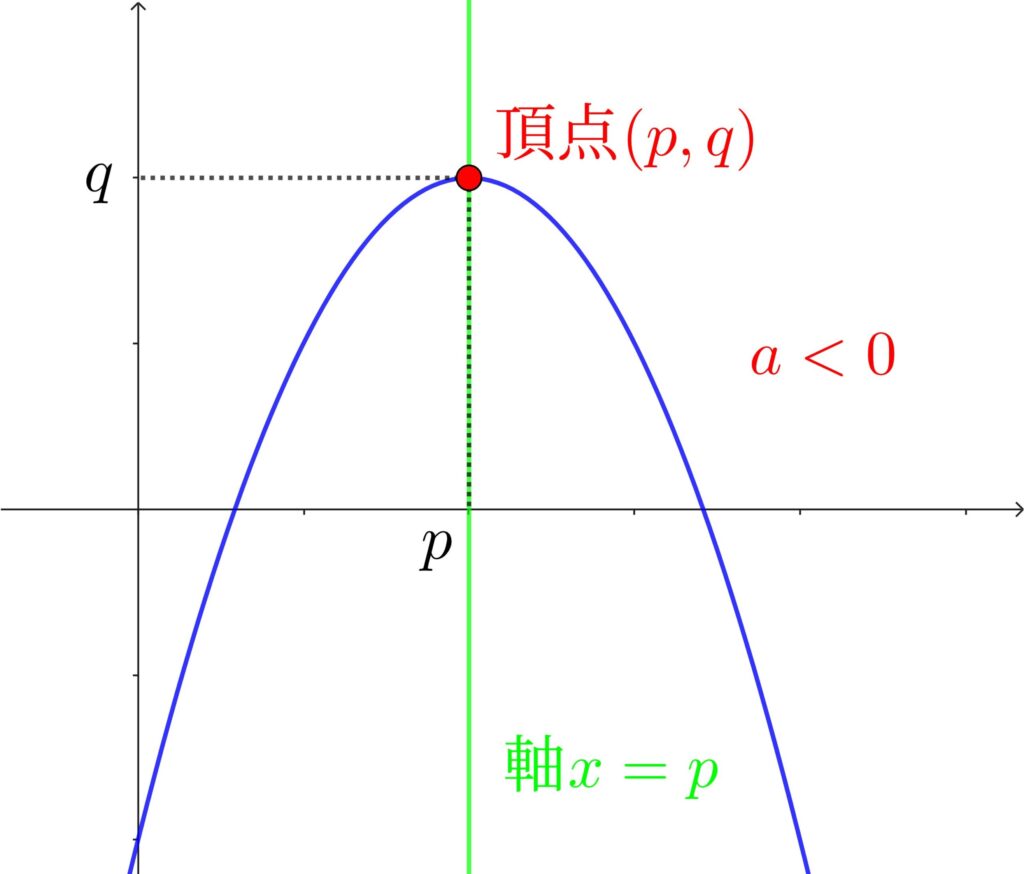
2次関数\(y=a{(x-p)}^2+q\) のグラフは、\(a>0\) のとき下に凸、\(a<0\) のとき上に凸の放物線になる。
また、頂点は \((p,q)\) 、軸は \(x=p\) の放物線である。

もっと詳しく願いします!!
こんにちは、現役教員の「さん」です。
「人より勉強に時間がかかる…」と悩んでいませんか?
私の学校でも、教科書の説明が難しくて止まってしまう生徒がたくさんいます。
• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」
• 「解答の意味が理解できず、勉強が進まない」
数学を理解するコツは、「自分なりに噛み砕いて考えること」。
このブログでは、皆さんの「つまずきポイント」を丁寧に噛み砕いて解説していきます!
2次関数のグラフ
中学の復習
まずは基本の形を思い出しましょう。
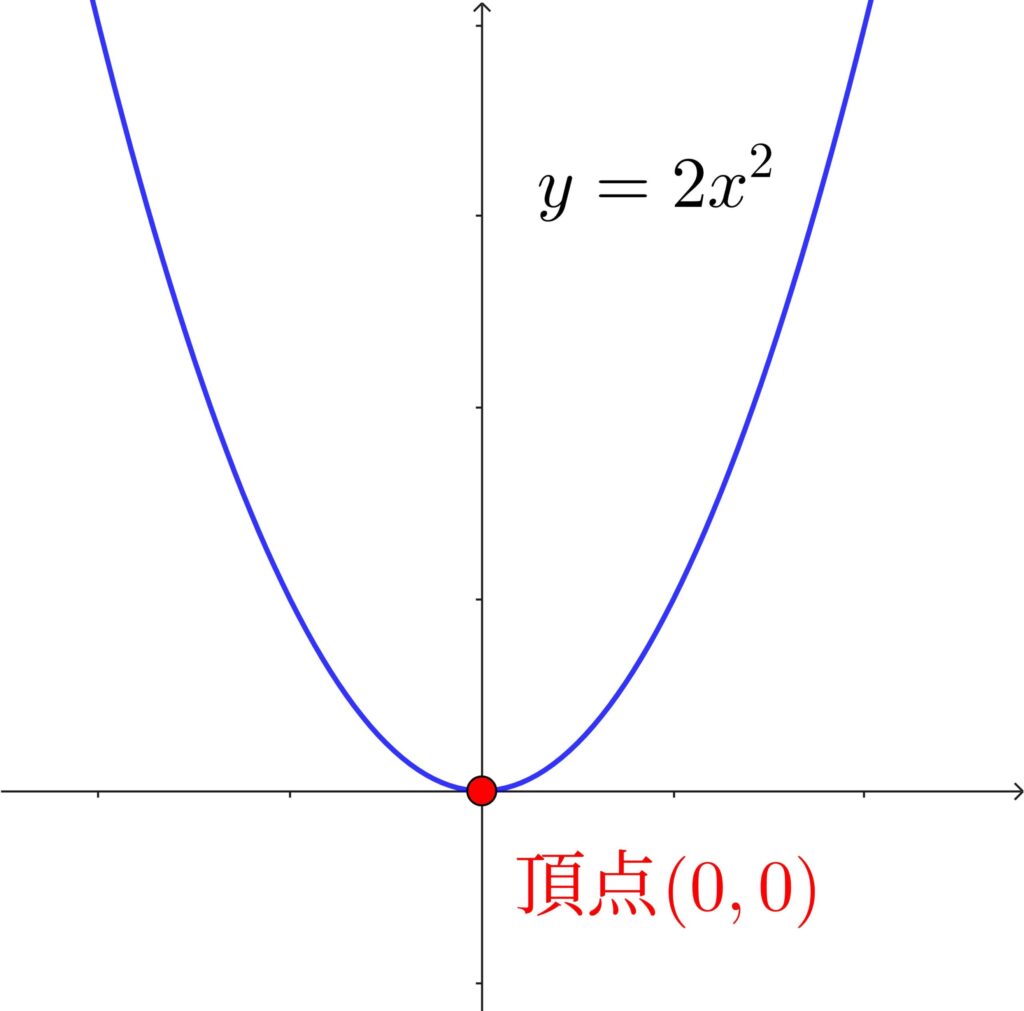
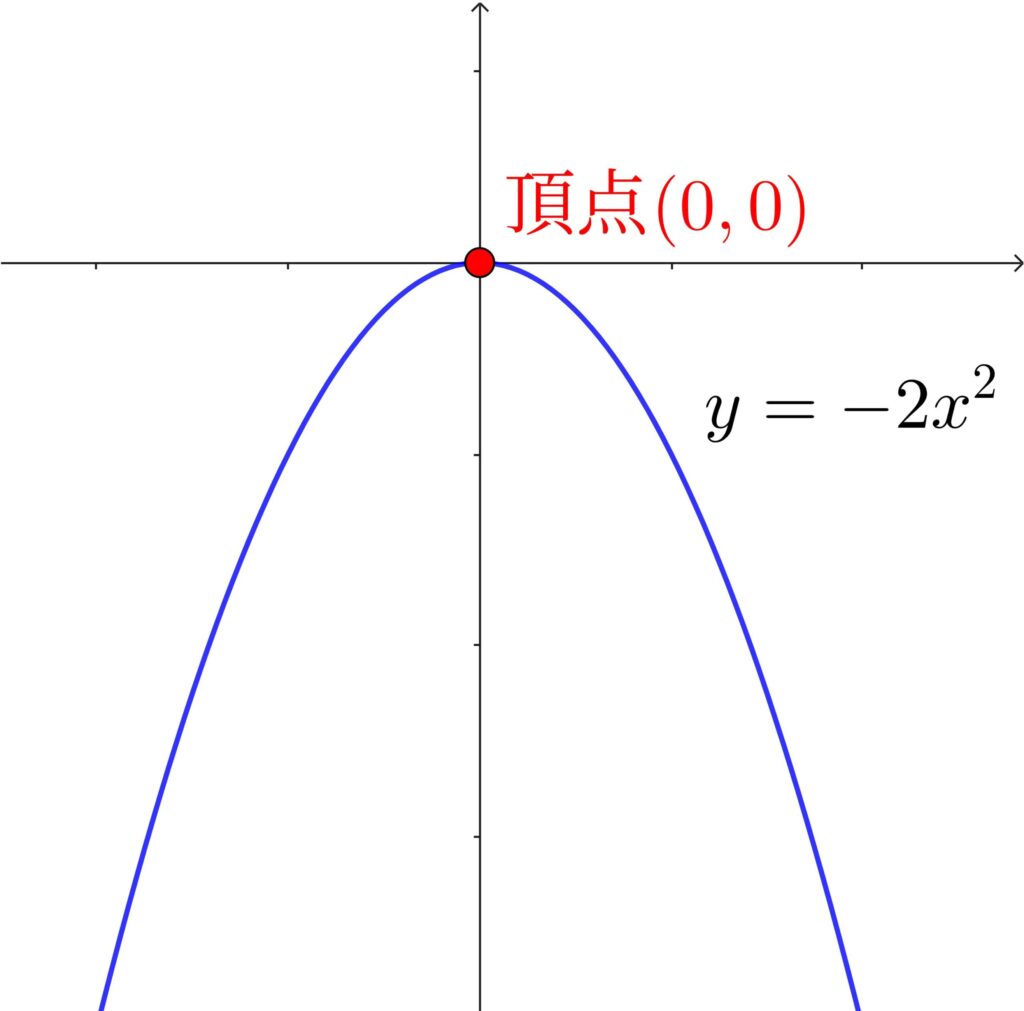
\(y=ax^2\) のグラフ
- 頂点:原点 \((0,0)\)
- 形:\(a>0\)(プラス)なら 「下に凸」の放物線
\(a<0\)(マイナス)なら 「上に凸」の放物線

そうだった。そうだった。ここまでは大丈夫。
グラフの「平行移動」
高校数学のメインテーマ、「平行移動」です。
\(y=ax^2\) のグラフをそのままスライドさせるには、数式を以下のように置き換えます。

\(\color{blue}{x→(x-p),\:y→(y-q)}\) という置換を行うと \(x\) 軸方向に \(p\)、\(y\) 軸方向に \(q\) 平行移動することができます。

\(+p\) 移動したいのに 、式では\(-p\) にするんだね。不思議。

理由は別の回で詳しく説明するけど、まずはこの「置き換えのルール」を型として覚えちゃおう!
\(\color{blue}{y}=a\color{blue}{x}^2\) の \(\color{blue}{x}\) と \(\color{blue}{y}\) を入れ替えると
\(\color{blue}{y-q}=a{(\color{blue}{x-q})}^2\)
これをきれいに整理すると
\(y=a{(x-q)}^2+q\)
この平行移動によって、頂点は原点\((0,0)\) から点 \((p,q)\) に移動移動します。

【実践】例題でマスターしよう
例題①:式をつくってみる
2次関数\(y=2x^2\) のグラフを、\(x\) 軸方向に \(2\)、\(y\) 軸方向に \(1\) だけ平行移動するとき、移動後の放物線の方程式を求めよ。
\(y=2x^2\) のグラフは、頂点 \((0,0)\) 、下に凸の放物線です。

\(\color{blue}{x→(x-2)}\) という置換を行うと、 \(x\) 軸方向に \(2\) 平行移動。
\(\color{blue}{y→(y-1)}\) という置換を行うと、 \(y\) 軸方向に \(1\) 平行移動。
\(\color{blue}{y-1}=2{(\color{blue}{x-2})}^2\)
整理すると、\(y=2{(x-2)}^2+1\)
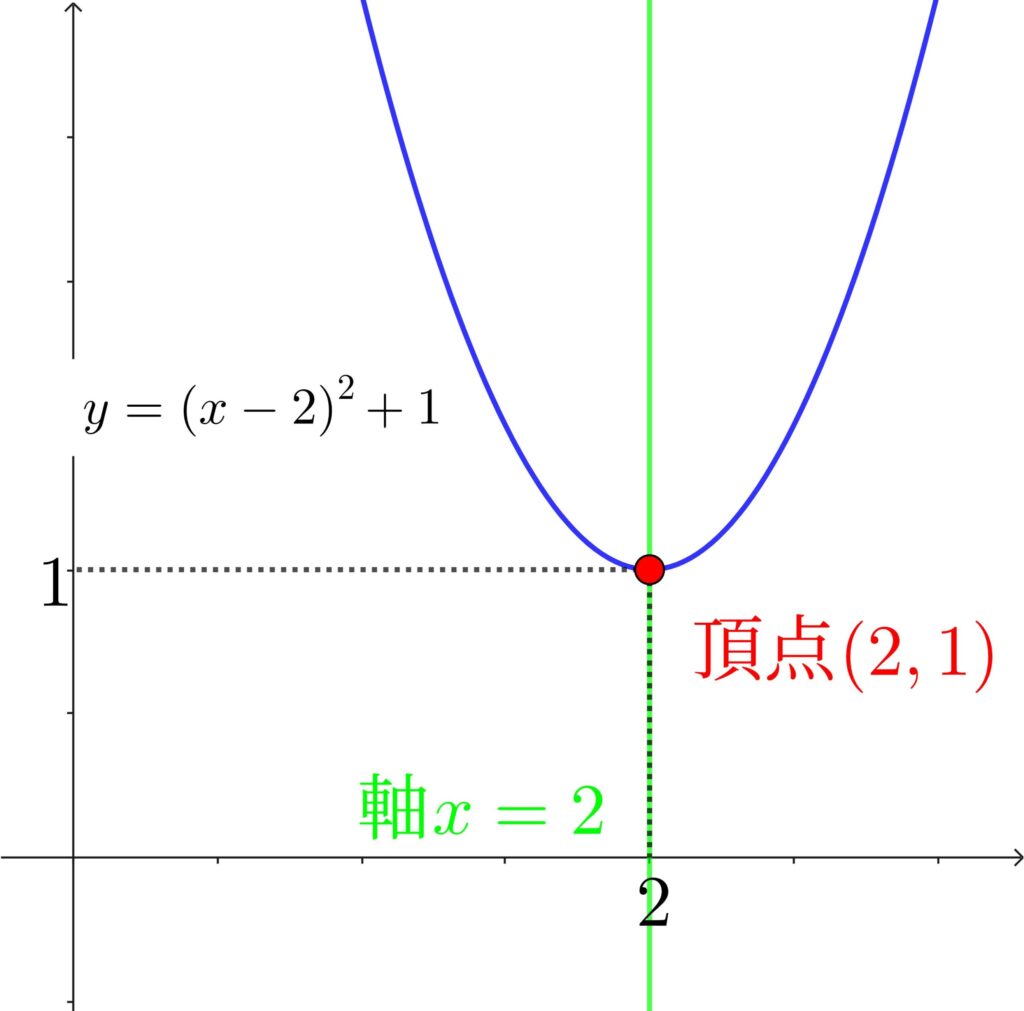
\(y=2{(x-2)}^2+1\)のグラフは、頂点 \((2,1)\) 、下に凸の放物線です。
例題②:グラフを描いてみる
2次関数 \(y=2(x-3)^2+1\) のグラフをかけ。また、その軸と頂点を求めよ。
\(y=2(x-3)^2+1\)は、\(y=2x^2\) のグラフを、\(x\) 軸方向に \(3\)、\(y\) 軸方向に \(1\) だけ平行移動したグラフです。
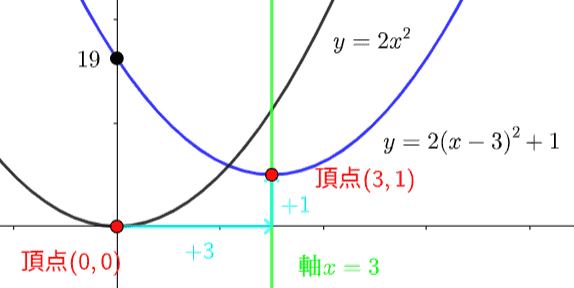
よって、頂点は \((3,1)\) となり、軸は放物線の真ん中の線のことで、頂点を通りますから \(x=3\) となります。

テストでグラフを描くときは、「頂点」と「\(y\) 軸との交点」の2か所に数値を書き込むのがルールだよ!

\(y=a{(x-q)}^2+q\) の形から、頂点 \((p,q)\)と軸 \(x=p\) がすぐ分かるようになりたいな!
まとめ:2次関数のグラフ

さて、今回のまとめだよ!
2次関数\(y=a{(x-p)}^2+q\) のグラフは、\(a>0\) のとき下に凸、\(a<0\) のとき上に凸の放物線になる。
また、頂点は \((p,q)\) 、軸は \(x=p\) の放物線である。



ありがとうございました!!






コメント