
今日の板書はこれ!
平方完成とは、\(ax^2+bx+c\) を \(a(x-p)^2+q\) に変形すること。
- \(x^2\) の係数でくくる (定数項(最後の数字)は無視!)
- カッコ内を2乗の形に (「半分」にして「2乗を引く」!)
- カッコを外して整理 (分配法則の計算ミスに注意!)

もっと詳しく願いします!!
こんにちは、現役教員の「さん」です。
「人より勉強に時間がかかる…」と悩んでいませんか?
私の学校でも、教科書の説明が難しくて止まってしまう生徒がたくさんいます。
• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」
• 「解答の意味が理解できず、勉強が進まない」
数学を理解するコツは、「自分なりに噛み砕いて考えること」。
このブログでは、皆さんの「つまずきポイント」を丁寧に噛み砕いて解説していきます!
平方完成ってなに?
平方完成とは、バラバラの形(一般形)を 頂点がわかる形(基本形) に変形することです。
\(ax^2+bx+c\) → \(a(x-p)^2+q\)
「難しそう…」と思うかもしれませんが、仕組みは意外とシンプル。
まずは「答えの形」から逆算して、構造を理解しましょう。
【準備】答えの形を展開してみよう
例として、\(2x^2-12x+19\) を平方完成すると \(2(x-3)^2+1\) になります。
まずは、この「答えの形」をバラバラに展開して、元の形に戻るか確認してみましょう。
① \((x-3)^2\) を展開する。
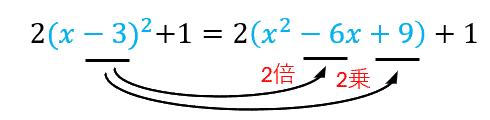

2乗の展開は、真ん中は「2倍」、後ろは「2乗」だったね!
② \(2(x^2-6x+9)\) を展開する
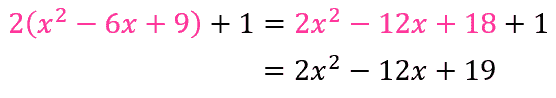
元の形に戻りましたね!平方完成は、今やった計算の「逆」をやるだけなんです。
【本番】平方完成の3ステップ
では、\(2x^2-12x+19\) を実際に平方完成していきましょう。
STEP 1:x がついている仲間だけを「くくる」
まず、\(x^2\) の前にある数字「2」に注目します。
後ろの数字「+19」は一旦無視します。
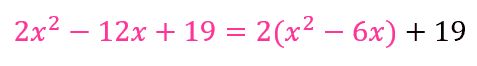
STEP 2:カッコの中を「無理やり2乗」にする
ここが一番の山場!
カッコの中を \((x – \text{数字})^2\) の形にします。
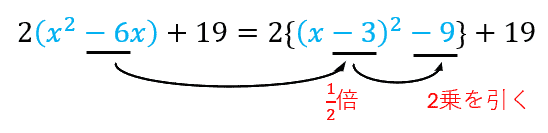
\(x\) の係数を半分にして、その2乗を引きます。
・ \(-6\) の半分は \(3\)
・ \(-3\) の2乗は \(9\) なので、\(9\) を引く

なんで \(9\)を引くの ?

\((x^2-6x+9)\) は \((x-3)^2\) なんだけど、\((-3)^2=9\) がないから \(9\) を引くんだ!
STEP 3:外の数字と合流させる
最後に、中カッコを外して数字をまとめます。
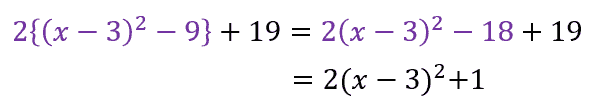

最後に残しておいた「19」を計算するのを忘れないようにね!
まとめ:2次関数のグラフ

さて、今回のまとめだよ!
平方完成とは、\(ax^2+bx+c\) を \(a(x-p)^2+q\) に変形すること。
- \(x^2\) の係数でくくる (定数項(最後の数字)は無視!)
- カッコ内を2乗の形に (「半分」にして「2乗を引く」!)
- カッコを外して整理 (分配法則の計算ミスに注意!)

ありがとうございました!!






コメント