
今日の板書はこれ!
- 平方完成をして \(y = a(x – p)^2 + q\) の形にする
- 頂点は \((p, q)\) 、軸は \(x = p\)
- \(y\) 軸との交点は「元の式」に \(x=0\) を入れて求める
軸の方程式:\(x=-\frac{b}{2a}\)

もっと詳しく願いします!!
こんにちは、現役教員の「さん」です。
「人より勉強に時間がかかる…」と悩んでいませんか?
私の学校でも、教科書の説明が難しくて止まってしまう生徒がたくさんいます。
• 「教科書や参考書の内容がわからなくて、読むのに時間がかかる」
• 「解答の意味が理解できず、勉強が進まない」
数学を理解するコツは、「自分なりに噛み砕いて考えること」。
このブログでは、皆さんの「つまずきポイント」を丁寧に噛み砕いて解説していきます!
y=ax^2+bx+c のグラフ
なぜ「平方完成」が必要なの?
結論から言うと、「頂点」を見つけたいからです。
- 一般形 \(y=ax^2+bx+c \) (このままだと頂点がどこか不明…)
- 基本形 \(y=(x-p)^2+q\) (パッと見て頂点 \((p, q)\) がわかる!)
\(y=ax^2+bx+c \) のグラフは、平方完成をして頂点を求めましょう。
例題でグラフ作成をマスターしよう!
2次関数 \(y=-2x^2-4x+1\) のグラフをかけ。 また、その軸と頂点を求めよ。
ステップ①:平方完成で「頂点」を出す
\(y=2x^2-4x+1\) を平方完成します。
これにより、頂点は\((-1,3)\)、軸は \(x=-1\) だとわかりました!
ステップ②:y軸との交点を求める
グラフをより正確にかくために、\(y\) 軸のどこを通るかも調べましょう。
\(x = 0\) を代入するだけです。

平方完成した後の式に代入してもいいけれど、「元の式(一般形)」に代入した方が一瞬で終わるよ!
\(y=-2\cdot 0^2-4x\cdot 0+1=1\)
つまり、点 \((0, 1)\) を通ることがわかります。
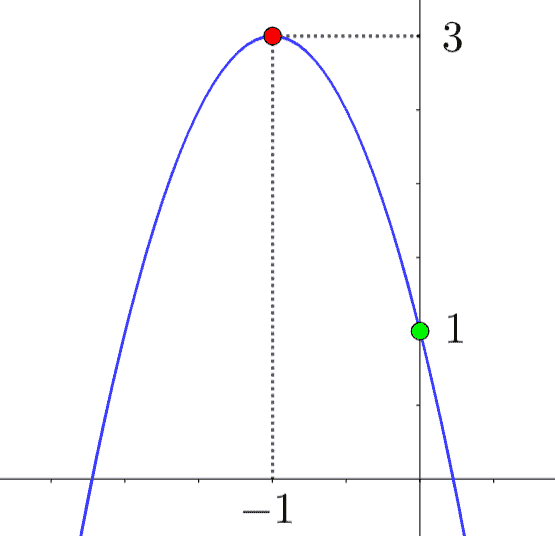
ステップ③:グラフを完成させる
求めた情報をグラフに書き込みます。
- 頂点 \((-1, 3)\) に点を打つ
- \(y\) 軸との交点 \((0, 1)\) に点を打つ
- \(x^2\) の係数がマイナスなので、「上に凸(山なり)」の形にする
【プラスα】平方完成しなくても「軸」がわかる公式?
実は、平方完成をわざわざしなくても、「軸」を一瞬で求める裏技があります。
\(y=ax^2+bx+c \) の軸の方程式:\(x=-\frac{b}{2a}\)

すごっ!!でも先生、なんでこれで求まるんですか?

良い質問だね!せっかくだから、文字式のまま平方完成をして、この公式を導き出してみよう。
よって2次関数 \(y=ax^2+bx+c \) の軸の方程式は \(x=-\frac{b}{2a}\)

共通テストなど、スピードが求められる場面ではこの公式がめちゃくちゃ役に立つよ。余裕がある人は覚えておこう!
まとめ:y=ax^2+bx+c のグラフ

さて、今回のまとめだよ!
- 平方完成をして \(y = a(x – p)^2 + q\) の形にする
- 頂点は \((p, q)\) 、軸は \(x = p\)
- \(y\) 軸との交点は「元の式」に \(x=0\) を入れて求める
軸の方程式:\(x=-\frac{b}{2a}\)

ありがとうございました!!






コメント