
今日の板書はこれ!
関数 \(y=f(x)\) を\(x\) 軸方向に \(p\)、\(y\) 軸方向に \(q\)平行移動した関数を \(y=g(x)\) とする。
\(g(x)\)の上の点 \((x,y)\) を逆に平行移動した点 \((x-p,y-q)\)
これを \(y=f(x)\) に代入した条件式 \(y-q=f(x-p)\) 、これが移動後の関数 \(y=g(x)\)。

もっと詳しく願いします!!
こんにちは、現役教員の「さん」です。
「\(x\) 軸方向に \(+2\) 移動するのに、なぜ式では \((x-2)\) になるんだろう?」
そう疑問に思ったことはありませんか?
私の教え子たちも、ここで「納得がいかない!」と立ち止まってしまう子がとても多いです。
•「公式として丸暗記しているけれど、理由は知らない」
• 「代入するときにプラスかマイナスか混乱する」
数学を理解するコツは、「自分なりに噛み砕いて考えること」。
今回は、平行移動の「なぜ?」を、根本から丁寧に解説していきます!
2次関数のグラフの平行移動の原理
平行移動のやり方(復習)
まずは、やり方をおさらいしましょう。
2次関数\(y=2x^2\) のグラフを、\(x\) 軸方向に \(2\)、\(y\) 軸方向に \(1\) だけ平行移動するとき、移動後の放物線の方程式を求めよ。
やり方は、変数を次のように「置き換える(置換する)」だけです。
- \(x\) を \((x – 2)\) に入れ替える
- \(y\) を \((y – 1)\) に入れ替える
すると、式はこうなります。
\(\color{pink}{y-1}=2{(\color{skyblue}{x-2})}^2\)
整理すると、おなじみの \(y=2{(x-2)}^2+1\) という形になりますね。

でも、右に「\(+2\)」動かしたいのに、式が「\(-2\)」になるのは、なんだか直感に反する気がしない?今回はその理由を解き明かすよ!
平行移動の原理
グラフとは「条件を満たす点の集まり」
平行移動を理解するために、まずは「グラフの本質」を知っておきましょう。
例えば、\(y = 2x\) というグラフ。
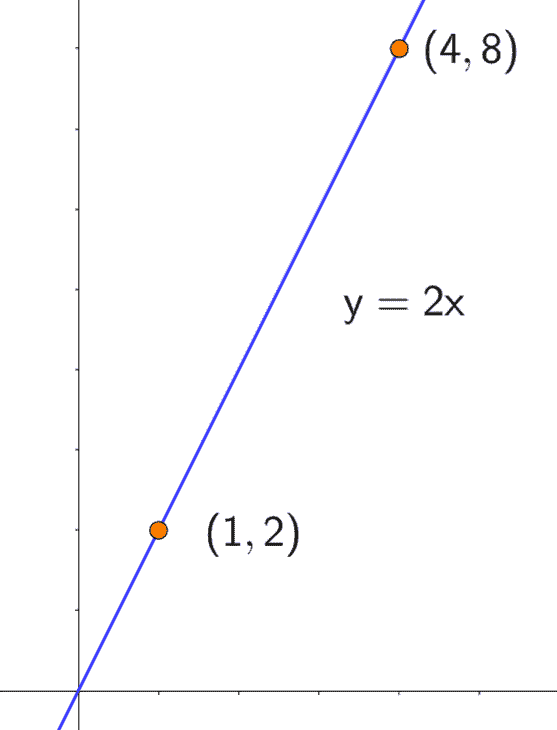
ここには、\((1, 2)\) や \((4, 8)\) といった点がありますが、これらはすべて 「\(y\) は \(x\) を2倍したもの」というルール(条件) を守っている点の集まりです。

「グラフの上にある点」は、式の「\(x\)」や「\(y\)」に代入できるってことだね!
\((1, 2)\) を代入すると、\(2 = 2\cdot 1\) より成り立つ。
\((4, 8)\) を代入しても、\(8 = 2\cdot 4\) より成り立つ。

その通り!逆に言えば、「点が守るべきルール」を数式にしたものが関数なんだ。
【核心】なぜ「逆」の符号を代入するのか?
いよいよ本題です。
元の関数を \(y = f(x)\)、移動後の関数を \(y = g(x)\) とします。
移動後の点 (x, y) の立場になって考える
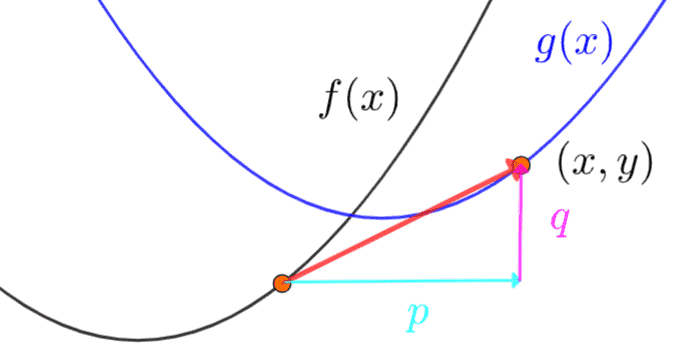
移動した後のグラフの上にある、ある点 \((x, y)\) 。
\(y = g(x)\) は、「この点 \((x, y)\) が守るべきルール」を数式にしたもののことです。
「元の世界」にタイムトラベルさせる
点 \((x, y)\) を、逆に \(x\) 軸方向に \(-p\)、\(y\) 軸方向に \(-q\) だけ戻してあげます。
すると、戻った先の点 \((x – p, y – q)\) は、移動前の「元の関数 \(y = f(x)\)」の上にぴったり重なるはずです。
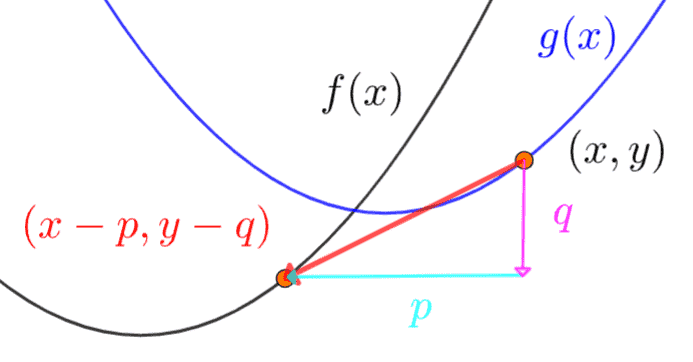
元のルールを借りてくる
戻った先の点は元の関数のルールを守っているので、代入すると計算が成り立ちます。
\(y-q=f(x-p)\)
これこそが、移動後の点 \((x, y)\) が満たす数式、 \(y = g(x)\) なのです!

なるほど!「移動後の点」を「元のルール」に当てはめるために、あえて逆に戻して代入しているから、符号がマイナスになるんだね!
まとめ:2次関数のグラフの平行移動の原理

さて、今回のまとめだよ!
関数 \(y=f(x)\) を\(x\) 軸方向に \(p\)、\(y\) 軸方向に \(q\)平行移動した関数を \(y=g(x)\) とする。
\(g(x)\)の上の点 \((x,y)\) を逆に平行移動した点 \((x-p,y-q)\)
これを \(y=f(x)\) に代入した条件式 \(y-q=f(x-p)\) 、これが移動後の関数 \(y=g(x)\)。

ありがとうございました!!






コメント